本文的网课内容学习自B站左程云老师的算法详解课程,旨在对其中的知识进行整理和分享~
一.区间dp可能性展开的常见方式
区间dp:大范围的问题拆分成若干小范围的问题来求解
可能性展开的常见方式:
1)基于两侧端点讨论的可能性展开
2)基于范围上划分点的可能性展开
二.让字符串成为回文串的最小插入次数
题目:让字符串成为回文串的最少插入次数

算法原理
-
整体原理
-
目标:通过最少的插入操作将任意字符串转换为回文串。
-
核心思想:
-
回文串性质:正读反读相同,对称性(如
"aba"、"abba")。 -
关键观察:字符串的最少插入次数 = 字符串长度 - 最长回文子序列(LPS)长度。
-
动态规划(DP):通过子问题的解构建全局解,避免重复计算。
-
-
-
具体步骤
-
方法1:暴力递归(分治法)
-
递归函数
f1(s, l, r):计算子串s[l..r]的最少插入次数。 -
基本情况:
-
单字符(
l == r):已是回文,返回0。 -
双字符(
l + 1 == r):相等则0,否则插入1次。
-
-
递归逻辑:
-
若
s[l] == s[r],则问题缩小为f1(s, l+1, r-1)。 -
否则,插入左或右字符,取最小值并
+1:-
Math.min(f1(s, l, r-1), f1(s, l+1, r)) + 1
-
-
-
-
方法2:记忆化搜索(自顶向下DP)
-
优化点:缓存子问题结果到
dp[l][r]数组,避免重复计算。 -
初始化:
dp初始为-1,表示未计算。 -
递归+缓存:
-
if (dp[l][r] != -1) return dp[l][r]; dp[l][r] = ans; // 存储结果
-
-
-
方法3:动态规划(自底向上DP)
-
填表顺序:从短子串向长子串递推(对角线填充)。
-
状态转移:
-
s[l] == s[r]:dp[l][r] = dp[l+1][r-1]。 -
s[l] != s[r]:dp[l][r] = min(dp[l][r-1], dp[l+1][r]) + 1。
-
-
示例填表(
s = "abca"):l\r
0 (a)
1 (b)
2 (c)
3 (a)
0
0
1
2
1
1
-
0
1
2
2
-
-
0
1
3
-
-
-
0
-
-
方法4:空间压缩(滚动数组)
-
优化空间:将二维
dp压缩为一维数组,仅保留必要状态。 -
关键变量:
-
leftDown:记录dp[l+1][r-1]。 -
backUp:临时保存dp[r]的旧值。
-
-
-
-
复杂度分析
-
时间复杂度:
-
暴力递归:O(2ⁿ)(指数级,超时)。
-
记忆化搜索 & DP:O(n²)(双重循环)。
-
-
空间复杂度:
-
记忆化搜索 & 二维DP:O(n²)。
-
空间压缩:O(n)。
-
-
-
示例
-
输入:
s = "abca" -
DP表填充:
-
初始化对角线
dp[i][i] = 0。 -
计算长度为2的子串:
-
dp = (a==b)? 0 : 1 = 1 -
dp = 1,dp = 1
-
-
计算长度为3的子串:
-
dp:a != c→min(dp, dp) + 1 = 2 -
dp:b != a→min(1, 1) + 1 = 2
-
-
计算全长
dp:-
a == a→dp = 1
-
-
- 输出:
1(插入"b"得到"abcba")。
-
-
总结
-
暴力递归:直观但效率低,适合小规模问题。
-
动态规划:通过状态转移方程高效求解,空间优化进一步提升性能。
-
应用场景:字符串处理、基因序列对齐等需对称性的问题。
-
关键点:
-
理解 回文子序列 与 插入操作 的关系。
-
掌握 DP状态定义 和 填表顺序。
-
-
-
代码实现
// 让字符串成为回文串的最少插入次数
// 给你一个字符串 s
// 每一次操作你都可以在字符串的任意位置插入任意字符
// 请你返回让s成为回文串的最少操作次数
// 测试链接 : https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/
public class Code01_MinimumInsertionToPalindrome {
// 暴力尝试
public static int minInsertions1(String str) {
char[] s = str.toCharArray();
int n = s.length;
return f1(s, 0, n - 1);
}
// s[l....r]这个范围上的字符串,整体都变成回文串
// 返回至少插入几个字符
public static int f1(char[] s, int l, int r) {
// l <= r
if (l == r) {
return 0;
}
if (l + 1 == r) {
return s[l] == s[r] ? 0 : 1;
}
// l...r不只两个字符
if (s[l] == s[r]) {
return f1(s, l + 1, r - 1);
} else {
return Math.min(f1(s, l, r - 1), f1(s, l + 1, r)) + 1;
}
}
// 记忆化搜索
public static int minInsertions2(String str) {
char[] s = str.toCharArray();
int n = s.length;
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
dp[i][j] = -1;
}
}
return f2(s, 0, n - 1, dp);
}
public static int f2(char[] s, int l, int r, int[][] dp) {
if (dp[l][r] != -1) {
return dp[l][r];
}
int ans;
if (l == r) {
ans = 0;
} else if (l + 1 == r) {
ans = s[l] == s[l + 1] ? 0 : 1;
} else {
if (s[l] == s[r]) {
ans = f2(s, l + 1, r - 1, dp);
} else {
ans = Math.min(f2(s, l, r - 1, dp), f2(s, l + 1, r, dp)) + 1;
}
}
dp[l][r] = ans;
return ans;
}
// 严格位置依赖的动态规划
public static int minInsertions3(String str) {
char[] s = str.toCharArray();
int n = s.length;
int[][] dp = new int[n][n];
for (int l = 0; l < n - 1; l++) {
dp[l][l + 1] = s[l] == s[l + 1] ? 0 : 1;
}
for (int l = n - 3; l >= 0; l--) {
for (int r = l + 2; r < n; r++) {
if (s[l] == s[r]) {
dp[l][r] = dp[l + 1][r - 1];
} else {
dp[l][r] = Math.min(dp[l][r - 1], dp[l + 1][r]) + 1;
}
}
}
return dp[0][n - 1];
}
// 空间压缩
// 本题有关空间压缩的实现,可以参考讲解067,题目4,最长回文子序列问题的讲解
// 这两个题空间压缩写法高度相似
// 因为之前的课多次讲过空间压缩的内容,所以这里不再赘述
public static int minInsertions4(String str) {
char[] s = str.toCharArray();
int n = s.length;
if (n < 2) {
return 0;
}
int[] dp = new int[n];
dp[n - 1] = s[n - 2] == s[n - 1] ? 0 : 1;
for (int l = n - 3, leftDown, backUp; l >= 0; l--) {
leftDown = dp[l + 1];
dp[l + 1] = s[l] == s[l + 1] ? 0 : 1;
for (int r = l + 2; r < n; r++) {
backUp = dp[r];
if (s[l] == s[r]) {
dp[r] = leftDown;
} else {
dp[r] = Math.min(dp[r - 1], dp[r]) + 1;
}
leftDown = backUp;
}
}
return dp[n - 1];
}
}三.预测赢家
题目:预测赢家

算法原理
-
整体原理
- 该问题属于博弈类动态规划问题,核心思想是:
- 玩家 1 和玩家 2 轮流从数组两端取数,每次取数后数组长度减 1。
- 玩家 1 先手,双方都采取最优策略(即每次选择让自己最终得分最大化)。
- 最终判断玩家 1 的得分是否 ≥ 玩家 2 的得分。
- 关键点:
- 由于双方都采取最优策略,当前玩家的选择会影响后续对手的选择。
- 可以用递归 + 动态规划模拟所有可能的取数路径,计算玩家 1 的最大可能得分。
- 该问题属于博弈类动态规划问题,核心思想是:
-
具体步骤
-
(1) 暴力递归(Brute Force)
- 定义递归函数
f(l, r):表示当前玩家在nums[l...r]范围内能获得的最大分数。 - 递归逻辑:
- 基本情况:
- 如果
l == r,只能选nums[l]。 - 如果
l + 1 == r,选较大的那个数(max(nums[l], nums[r]))。
- 如果
- 一般情况:
- 当前玩家有两种选择:
- 选左端
nums[l]:对手在[l+1, r]范围内采取最优策略,当前玩家剩余分数为nums[l] + min(f(l+2, r), f(l+1, r-1))(对手会留下较小的分数)。 - 选右端
nums[r]:同理,剩余分数为nums[r] + min(f(l, r-2), f(l+1, r-1))。
- 选左端
- 取两种选择的最大值作为当前玩家的最优解。
- 当前玩家有两种选择:
- 基本情况:
- 定义递归函数
-
(2) 记忆化搜索(Memoization)
- 优化递归:避免重复计算,用
dp[l][r]记录f(l, r)的结果。 - 初始化
dp表:初始值为-1,表示未计算。 - 递归时先查表:如果
dp[l][r] != -1,直接返回结果。
- 优化递归:避免重复计算,用
-
(3) 动态规划(DP)
- 填表顺序:从小区间到大区间(
l从后往前,r从前往后)。 - 状态转移:
dp[l][r] = max( nums[l] + min(dp[l+2][r], dp[l+1][r-1]), nums[r] + min(dp[l][r-2], dp[l+1][r-1]) ) - 最终结果:
dp[n-1]是玩家 1 的最大得分,判断是否 ≥ 总分数的一半。
- 填表顺序:从小区间到大区间(
-
-
复杂度分析
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
|
- 暴力递归:指数级复杂度,重复计算严重。
- 记忆化搜索 & DP:通过填表避免重复计算,优化为多项式时间。
-
示例
- 输入:
nums = [1, 5, 2] - 总分数:
1 + 5 + 2 = 8 - DP 填表过程:
- 初始化
dp[i][i] = nums[i]:dp = 1,dp = 5,dp = 2。
- 计算长度为 2 的区间:
dp = max(1, 5) = 5dp = max(5, 2) = 5
- 计算长度为 3 的区间
dp:- 选左端 1:对手留下
min(dp, dp) = min(2, 5) = 2→ 得分1 + 2 = 3。 - 选右端 2:对手留下
min(dp, dp) = min(1, 5) = 1→ 得分2 + 1 = 3。 dp = max(3, 3) = 3(玩家 1 最高得分)。
- 选左端 1:对手留下
- 初始化
- 结果:
3 ≥ 8/2→true。
- 输入:
-
总结
- 核心思想:博弈问题中,当前玩家的最优选择需考虑对手的反制策略。
- 优化方法:暴力递归 → 记忆化搜索 → 动态规划,逐步降低时间复杂度。
- 适用场景:类似“石子游戏”、“硬币取数”等博弈问题。
- 关键点:
- 定义
dp[l][r]表示区间[l, r]的最优解。 - 状态转移时,用
min模拟对手的优化选择。
- 定义
- 最终结论:动态规划是解决此类问题的标准方法,兼顾效率和清晰性。
代码实现
// 预测赢家
// 给你一个整数数组 nums 。玩家 1 和玩家 2 基于这个数组设计了一个游戏
// 玩家 1 和玩家 2 轮流进行自己的回合,玩家 1 先手
// 开始时,两个玩家的初始分值都是 0
// 每一回合,玩家从数组的任意一端取一个数字
// 取到的数字将会从数组中移除,数组长度减1
// 玩家选中的数字将会加到他的得分上
// 当数组中没有剩余数字可取时游戏结束
// 如果玩家 1 能成为赢家,返回 true
// 如果两个玩家得分相等,同样认为玩家 1 是游戏的赢家,也返回 true
// 你可以假设每个玩家的玩法都会使他的分数最大化
// 测试链接 : https://leetcode.cn/problems/predict-the-winner/
public class Code02_PredictTheWinner {
// 暴力尝试
public static boolean predictTheWinner1(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
int n = nums.length;
int first = f1(nums, 0, n - 1);
int second = sum - first;
return first >= second;
}
// nums[l...r]范围上的数字进行游戏,轮到玩家1
// 返回玩家1最终能获得多少分数,玩家1和玩家2都绝顶聪明
public static int f1(int[] nums, int l, int r) {
if (l == r) {
return nums[l];
}
if (l == r - 1) {
return Math.max(nums[l], nums[r]);
}
// l....r 不只两个数
// 可能性1 :玩家1拿走nums[l] l+1...r
int p1 = nums[l] + Math.min(f1(nums, l + 2, r), f1(nums, l + 1, r - 1));
// 可能性2 :玩家1拿走nums[r] l...r-1
int p2 = nums[r] + Math.min(f1(nums, l + 1, r - 1), f1(nums, l, r - 2));
return Math.max(p1, p2);
}
// 记忆化搜索
public static boolean predictTheWinner2(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
int n = nums.length;
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
dp[i][j] = -1;
}
}
int first = f2(nums, 0, n - 1, dp);
int second = sum - first;
return first >= second;
}
public static int f2(int[] nums, int l, int r, int[][] dp) {
if (dp[l][r] != -1) {
return dp[l][r];
}
int ans;
if (l == r) {
ans = nums[l];
} else if (l == r - 1) {
ans = Math.max(nums[l], nums[r]);
} else {
int p1 = nums[l] + Math.min(f2(nums, l + 2, r, dp), f2(nums, l + 1, r - 1, dp));
int p2 = nums[r] + Math.min(f2(nums, l + 1, r - 1, dp), f2(nums, l, r - 2, dp));
ans = Math.max(p1, p2);
}
dp[l][r] = ans;
return ans;
}
// 严格位置依赖的动态规划
public static boolean predictTheWinner3(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
int n = nums.length;
int[][] dp = new int[n][n];
for (int i = 0; i < n - 1; i++) {
dp[i][i] = nums[i];
dp[i][i + 1] = Math.max(nums[i], nums[i + 1]);
}
dp[n - 1][n - 1] = nums[n - 1];
for (int l = n - 3; l >= 0; l--) {
for (int r = l + 2; r < n; r++) {
dp[l][r] = Math.max(
nums[l] + Math.min(dp[l + 2][r], dp[l + 1][r - 1]),
nums[r] + Math.min(dp[l + 1][r - 1], dp[l][r - 2]));
}
}
int first = dp[0][n - 1];
int second = sum - first;
return first >= second;
}
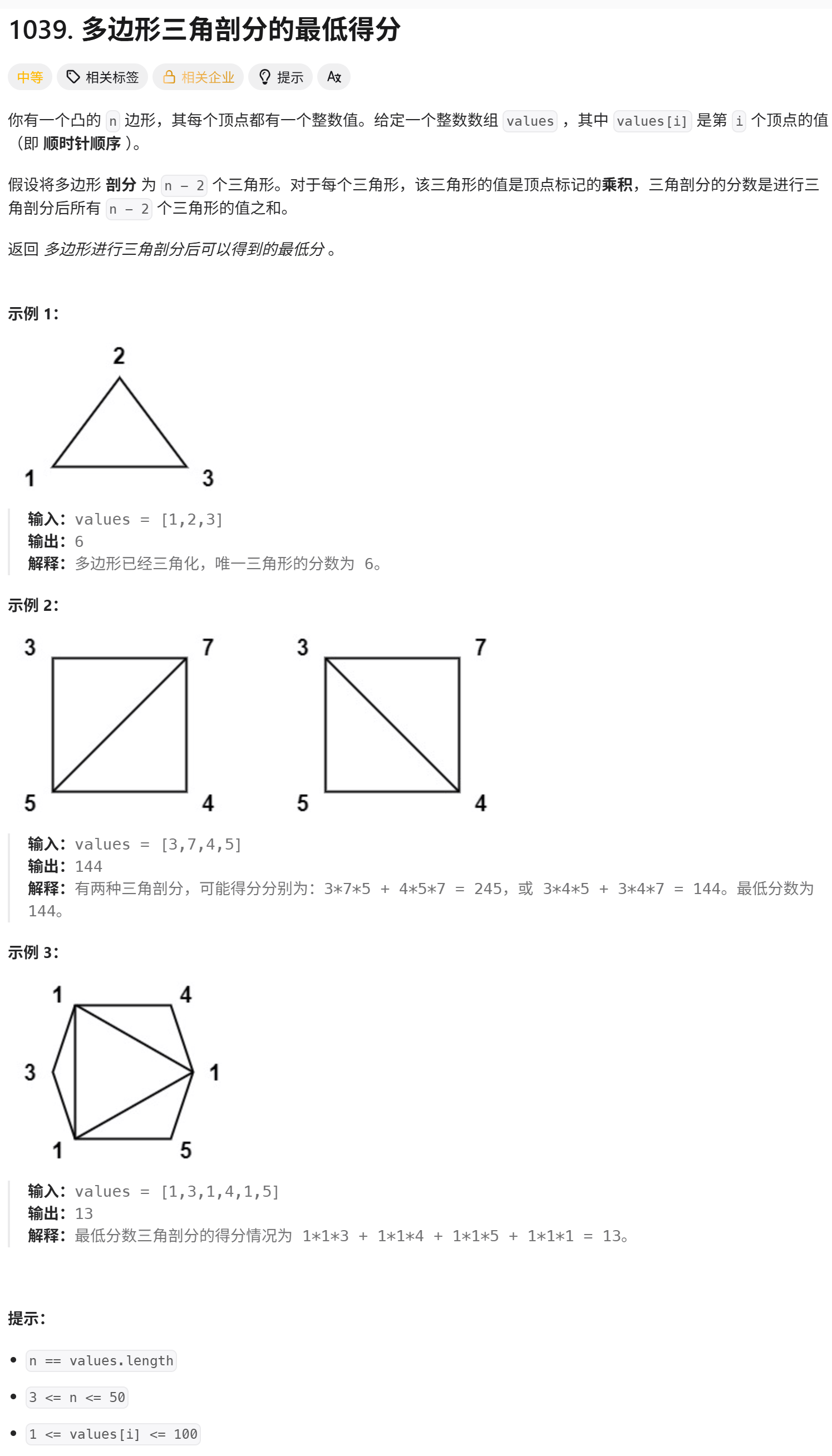
}四.多边形三角剖分的最低得分
题目:多边形三角剖分的最低得分
算法原理
-
整体原理
-
凸多边形性质:任意一条对角线(不相交的边)可将多边形分成两个子多边形。
-
动态规划思路:
-
定义
dp[l][r]表示顶点l到r的子多边形的最低三角剖分得分。 -
通过枚举所有可能的中间顶点
m,将多边形[l...r]拆分为:-
子多边形
[l...m]。 -
子多边形
[m...r]。 -
当前三角形
(l, m, r),其得分为values[l] * values[m] * values[r]。
-
-
状态转移方程:dp[l][r] = min( dp[l][m] + dp[m][r] + values[l] * values[m] * values[r] for all m in (l+1, r-1) )
-
-
-
具体步骤
- (1) 记忆化搜索(Top-Down DP)
-
初始化
dp表:所有dp[l][r]初始为-1(未计算)。 -
递归函数
f(l, r):-
基本情况:
-
如果
l == r或l == r-1,得分为 0(无法形成三角形)。
-
-
递归情况:
-
枚举中间点
m(l < m < r),计算:score = f(l, m) + f(m, r) + values[l] * values[m] * values[r] - 取所有 `m` 的最小 `score` 作为 `dp[l][r]`。
-
-
- 返回结果:
f(0, n-1)是整个多边形的最低得分。
-
- (2) 动态规划(Bottom-Up DP)
-
填表顺序:
-
l从大到小(n-3到0)。 -
r从小到大(l+2到n-1)。 -
确保计算
dp[l][r]时,dp[l][m]和dp[m][r]已计算。
-
-
状态转移:
-
对于每个
(l, r),枚举m并更新: - dp[l][r] = min(dp[l][r], dp[l][m] + dp[m][r] + values[l] * values[m] * values[r])
-
-
最终结果:
dp[n-1]是最低得分。
-
- (1) 记忆化搜索(Top-Down DP)
-
复杂度分析
|
|
|
|---|---|---|
|
|
|
|
|
|
-
三重循环:外层
l、中层r、内层m,共 O(n³)。 -
空间优化:
dp表为 O(n²)。 -
示例
- 输入:
values = [1, 3, 1, 4, 1, 5] - 填表过程:
-
初始化
dp[i][i] = 0,dp[i][i+1] = 0。 -
计算
dp:-
m = 1:得分0 + 0 + 1*3*1 = 3→dp = 3。
-
-
计算
dp:-
m = 2:得分0 + 0 + 3*1*4 = 12→dp = 12。
-
-
计算
dp:-
m = 1:得分0 + 12 + 1*3*4 = 24。 -
m = 2:得分3 + 0 + 1*1*4 = 7→dp = 7。
-
-
最终结果:
dp是所有剖分中的最小值。
-
- 输入:
-
总结
-
核心思想:通过动态规划枚举所有可能的三角剖分,利用子问题最优解构造全局最优解。
-
关键点:
-
状态定义:
dp[l][r]表示子多边形的最低得分。 -
状态转移:枚举中间点
m,拆分问题为两个子问题。
-
-
适用场景:凸多边形划分、矩阵链乘法等类似问题。
-
代码实现
// 多边形三角剖分的最低得分
// 你有一个凸的 n 边形,其每个顶点都有一个整数值
// 给定一个整数数组values,其中values[i]是第i个顶点的值(顺时针顺序)
// 假设将多边形 剖分 为 n - 2 个三角形
// 对于每个三角形,该三角形的值是顶点标记的乘积
// 三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和
// 返回 多边形进行三角剖分后可以得到的最低分
// 测试链接 : https://leetcode.cn/problems/minimum-score-triangulation-of-polygon/
public class Code03_MinimumScoreTriangulationOfPolygon {
// 记忆化搜索
public static int minScoreTriangulation1(int[] arr) {
int n = arr.length;
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = -1;
}
}
return f(arr, 0, n - 1, dp);
}
public static int f(int[] arr, int l, int r, int[][] dp) {
if (dp[l][r] != -1) {
return dp[l][r];
}
int ans = Integer.MAX_VALUE;
if (l == r || l == r - 1) {
ans = 0;
} else {
// l....r >=3
// 0..1..2..3..4...5
for (int m = l + 1; m < r; m++) {
// l m r
ans = Math.min(ans, f(arr, l, m, dp) + f(arr, m, r, dp) + arr[l] * arr[m] * arr[r]);
}
}
dp[l][r] = ans;
return ans;
}
// 严格位置依赖的动态规划
public static int minScoreTriangulation2(int[] arr) {
int n = arr.length;
int[][] dp = new int[n][n];
for (int l = n - 3; l >= 0; l--) {
for (int r = l + 2; r < n; r++) {
dp[l][r] = Integer.MAX_VALUE;
for (int m = l + 1; m < r; m++) {
dp[l][r] = Math.min(dp[l][r], dp[l][m] + dp[m][r] + arr[l] * arr[m] * arr[r]);
}
}
}
return dp[0][n - 1];
}
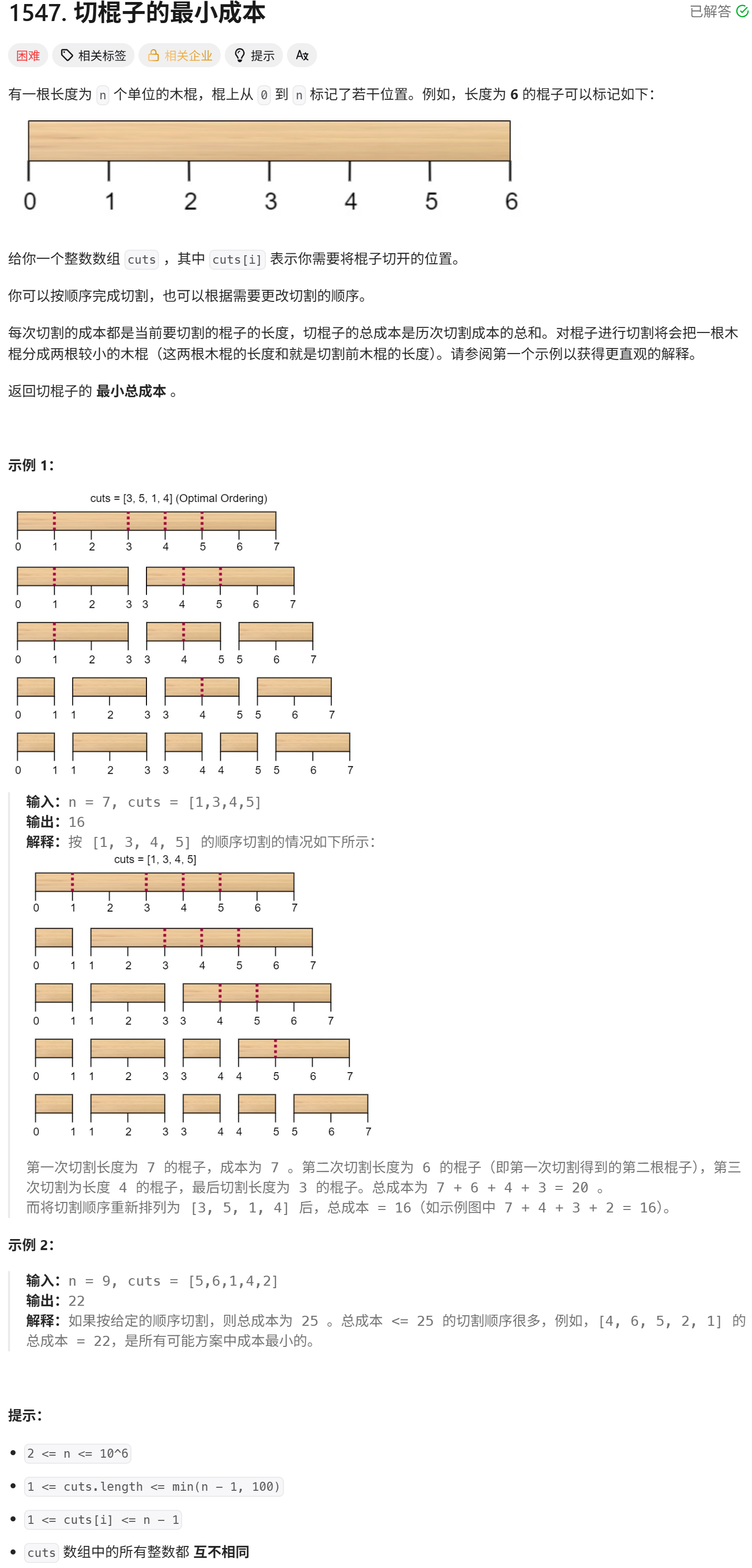
}五.切棍子的最小成本
题目:切棍子的最小成本
算法原理
-
整体原理
-
切割顺序影响总成本:不同的切割顺序会导致不同的中间木棍长度,从而影响总成本。
-
动态规划思路:
-
将切割位置排序后,定义
dp[l][r]表示处理切割点l到r的最小成本。 -
每次选择一个切割点
k,将问题分解为左半部分[l, k-1]和右半部分[k+1, r]。 -
当前切割成本为当前木棍长度
arr[r+1] - arr[l-1]。
-
-
-
具体步骤
-
(1) 记忆化搜索(Top-Down DP)
-
预处理:
-
将
cuts排序,并在首尾添加0和n,形成arr数组。
-
-
递归函数
f(l, r):-
基本情况:
-
如果
l > r,返回0(无需切割)。 -
如果
l == r,返回arr[r+1] - arr[l-1](单个切割点的成本)。
-
-
递归情况:
-
枚举切割点
k(l ≤ k ≤ r),计算:cost = f(l, k-1) + f(k+1, r) + arr[r+1] - arr[l-1]
-
-
取所有 `k` 的最小 `cost` 作为 `dp[l][r]`。
-
-
返回结果:
f(1, m),其中m是cuts的长度。
-
-
(2) 动态规划(Bottom-Up DP)
-
初始化:
-
dp[i][i] = arr[i+1] - arr[i-1](单个切割点的成本)。
-
-
填表顺序:
-
l从大到小(m-1到1)。 -
r从小到大(l+1到m)。
-
-
状态转移:
-
对于每个
(l, r),枚举k并更新:dp[l][r] = arr[r+1] - arr[l-1] + min(dp[l][k-1] + dp[k+1][r])
-
-
最终结果:
dp[m]是最小总成本。
-
-
-
复杂度分析
|
|
|
|---|---|---|
|
|
|
|
|
|
-
三重循环:外层
l、中层r、内层k,共 O(m³)。 -
空间优化:
dp表为 O(m²)。 -
示例
-
输入:
n = 7,cuts = [1, 3, 4, 5] -
预处理:
arr = [0, 1, 3, 4, 5, 7] -
填表过程:
-
初始化
dp = 1-0 + 3-1 = 3(实际应为arr-arr=3)。 -
计算
dp:-
k=1:dp + dp + 4-0 = 0 + (5-1) + 4 = 8。 -
k=2:dp + dp + 4-0 = 3 + 0 + 4 = 7。 -
dp = min(8, 7) = 7。
-
-
最终结果:
dp是所有切割顺序中的最小成本。
-
-
-
总结
-
核心思想:通过动态规划枚举所有切割顺序,利用子问题最优解构造全局最优解。
-
关键点:
-
状态定义:
dp[l][r]表示处理切割点l到r的最小成本。 -
状态转移:枚举切割点
k,拆分问题为左右子问题。
-
-
适用场景:类似切割问题、区间划分问题。
-
代码实现
import java.util.Arrays;
// 切棍子的最小成本
// 有一根长度为n个单位的木棍,棍上从0到n标记了若干位置
// 给你一个整数数组cuts,其中cuts[i]表示你需要将棍子切开的位置
// 你可以按顺序完成切割,也可以根据需要更改切割的顺序
// 每次切割的成本都是当前要切割的棍子的长度,切棍子的总成本是历次切割成本的总和
// 对棍子进行切割将会把一根木棍分成两根较小的木棍
// 这两根木棍的长度和就是切割前木棍的长度
// 返回切棍子的最小总成本
// 测试链接 : https://leetcode.cn/problems/minimum-cost-to-cut-a-stick/
public class Code04_MinimumCostToCutAStick {
// 记忆化搜索
public static int minCost1(int n, int[] cuts) {
int m = cuts.length;
Arrays.sort(cuts);
int[] arr = new int[m + 2];
arr[0] = 0;
for (int i = 1; i <= m; ++i) {
arr[i] = cuts[i - 1];
}
arr[m + 1] = n;
int[][] dp = new int[m + 2][m + 2];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= m; j++) {
dp[i][j] = -1;
}
}
return f(arr, 1, m, dp);
}
// 切点[l....r],决定一个顺序
// 让切点都切完,总代价最小
public static int f(int[] arr, int l, int r, int[][] dp) {
if (l > r) {
return 0;
}
if (l == r) {
return arr[r + 1] - arr[l - 1];
}
if (dp[l][r] != -1) {
return dp[l][r];
}
int ans = Integer.MAX_VALUE;
for (int k = l; k <= r; k++) {
ans = Math.min(ans, f(arr, l, k - 1, dp) + f(arr, k + 1, r, dp));
}
ans += arr[r + 1] - arr[l - 1];
dp[l][r] = ans;
return ans;
}
// 严格位置依赖的动态规划
public static int minCost2(int n, int[] cuts) {
int m = cuts.length;
Arrays.sort(cuts);
int[] arr = new int[m + 2];
arr[0] = 0;
for (int i = 1; i <= m; ++i) {
arr[i] = cuts[i - 1];
}
arr[m + 1] = n;
int[][] dp = new int[m + 2][m + 2];
for (int i = 1; i <= m; i++) {
dp[i][i] = arr[i + 1] - arr[i - 1];
}
for (int l = m - 1, next; l >= 1; l--) {
for (int r = l + 1; r <= m; r++) {
next = Integer.MAX_VALUE;
for (int k = l; k <= r; k++) {
next = Math.min(next, dp[l][k - 1] + dp[k + 1][r]);
}
dp[l][r] = arr[r + 1] - arr[l - 1] + next;
}
}
return dp[1][m];
}
}六.戳气球
题目:戳气球

算法原理
-
整体原理
-
逆向思考:考虑最后一个被戳破的气球,将问题分解为左右子区间。
-
动态规划:
-
定义
dp[l][r]表示戳破[l...r]区间内气球的最大硬币数。 -
枚举区间内每个气球
k作为最后一个戳破的,计算:coins = nums[l-1] * nums[k] * nums[r+1] + dp[l][k-1] + dp[k+1][r] -
取所有
k的最大coins作为dp[l][r]。
-
-
-
具体步骤
-
(1) 记忆化搜索(Top-Down DP)
-
预处理:
-
在
nums首尾添加1,形成arr数组。
-
-
递归函数
f(l, r):-
基本情况:
l == r时,直接返回arr[l-1] * arr[l] * arr[l+1]。 -
递归情况:
-
选择
l或r作为最后一个戳破的:max(arr[l-1]*arr[l]*arr[r+1] + f(l+1, r), arr[l-1]*arr[r]*arr[r+1] + f(l, r-1)) -
枚举中间 `k`:max(f(l, k-1) + arr[l-1]*arr[k]*arr[r+1] + f(k+1, r))
-
返回结果:
f(1, n)。
-
-
-
-
(2) 动态规划(Bottom-Up DP)
-
初始化:
-
dp[i][i] = arr[i-1] * arr[i] * arr[i+1]。
-
-
填表顺序:
-
l从n到1,r从l+1到n。
-
-
状态转移:
-
对于每个
(l, r),计算:dp[l][r] = max( arr[l-1]*arr[l]*arr[r+1] + dp[l+1][r], arr[l-1]*arr[r]*arr[r+1] + dp[l][r-1], max_{k=l+1}^{r-1} (dp[l][k-1] + arr[l-1]*arr[k]*arr[r+1] + dp[k+1][r]) )
-
-
最终结果:
dp[n]。
-
-
-
复杂度分析
|
|
|
|---|---|---|
|
|
|
|
|
|
-
示例
-
输入:
nums = [3, 1, 5, 8] -
预处理:
arr = [1, 3, 1, 5, 8, 1] -
填表过程:
-
初始化
dp = 1*3*1 = 3,dp = 3*1*5 = 15,dp = 1*5*8 = 40,dp = 5*8*1 = 40。 -
计算
dp:-
k=1:0 + 1*3*5 + 15 = 30。 -
k=2:3 + 1*1*5 + 0 = 8。 -
dp = max(30, 8) = 30。
-
-
最终结果:
dp = 167(最优顺序:1 → 5 → 3 → 8 → 1)。
-
-
总结
-
核心思想:逆向思维 + 区间DP,通过枚举最后一个戳破的气球分解问题。
-
关键点:
-
状态定义:
dp[l][r]表示区间[l, r]的最大硬币数。 -
状态转移:枚举最后一个戳破的气球
k,合并左右子区间结果。
-
-
适用场景:区间分割、最优顺序问题(如矩阵链乘法)。
-
注:实际实现时需注意边界处理(
l > r时返回0)。
-
代码实现
// 戳气球
// 有 n 个气球,编号为0到n-1,每个气球上都标有一个数字,这些数字存在数组nums中
// 现在要求你戳破所有的气球。戳破第 i 个气球
// 你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币
// 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号
// 如果 i - 1或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球
// 求所能获得硬币的最大数量
// 测试链接 : https://leetcode.cn/problems/burst-balloons/
public class Code05_BurstBalloons {
// 记忆化搜索
public static int maxCoins1(int[] nums) {
int n = nums.length;
// a b c d e
// 1 a b c d e 1
int[] arr = new int[n + 2];
arr[0] = 1;
arr[n + 1] = 1;
for (int i = 0; i < n; i++) {
arr[i + 1] = nums[i];
}
int[][] dp = new int[n + 2][n + 2];
for (int i = 1; i <= n; i++) {
for (int j = i; j <= n; j++) {
dp[i][j] = -1;
}
}
return f(arr, 1, n, dp);
}
// arr[l...r]这些气球决定一个顺序,获得最大得分返回!
// 一定有 : arr[l-1]一定没爆!
// 一定有 : arr[r+1]一定没爆!
// 尝试每个气球最后打爆
public static int f(int[] arr, int l, int r, int[][] dp) {
if (dp[l][r] != -1) {
return dp[l][r];
}
int ans;
if (l == r) {
ans = arr[l - 1] * arr[l] * arr[r + 1];
} else {
// l ....r
// l +1 +2 .. r
ans = Math.max(
arr[l - 1] * arr[l] * arr[r + 1] + f(arr, l + 1, r, dp), // l位置的气球最后打爆
arr[l - 1] * arr[r] * arr[r + 1] + f(arr, l, r - 1, dp));// r位置的气球最后打爆
for (int k = l + 1; k < r; k++) {
// k位置的气球最后打爆
// l...k-1 k k+1...r
ans = Math.max(ans, arr[l - 1] * arr[k] * arr[r + 1] + f(arr, l, k - 1, dp) + f(arr, k + 1, r, dp));
}
}
dp[l][r] = ans;
return ans;
}
// 严格位置依赖的动态规划
public static int maxCoins2(int[] nums) {
int n = nums.length;
int[] arr = new int[n + 2];
arr[0] = 1;
arr[n + 1] = 1;
for (int i = 0; i < n; i++) {
arr[i + 1] = nums[i];
}
int[][] dp = new int[n + 2][n + 2];
for (int i = 1; i <= n; i++) {
dp[i][i] = arr[i - 1] * arr[i] * arr[i + 1];
}
for (int l = n, ans; l >= 1; l--) {
for (int r = l + 1; r <= n; r++) {
ans = Math.max(arr[l - 1] * arr[l] * arr[r + 1] + dp[l + 1][r],
arr[l - 1] * arr[r] * arr[r + 1] + dp[l][r - 1]);
for (int k = l + 1; k < r; k++) {
ans = Math.max(ans, arr[l - 1] * arr[k] * arr[r + 1] + dp[l][k - 1] + dp[k + 1][r]);
}
dp[l][r] = ans;
}
}
return dp[1][n];
}
}七.布尔运算
题目:布尔运算

算法原理
-
整体原理
-
分治思想:将表达式按逻辑运算符拆分为左右两部分,递归计算左右子表达式的可能结果。
-
动态规划:
-
定义
dp[l][r][0/1]表示子表达式s[l...r]计算结果为0或1的方法数。 -
枚举每个逻辑运算符作为最后计算的运算符,合并左右子结果。
-
-
-
具体步骤
- (1) 记忆化搜索(Top-Down DP)
-
递归函数
f(l, r):-
输入:子表达式
s[l...r]。 -
输出:长度为 2 的数组
[f, t],其中f是结果为0的方法数,t是结果为1的方法数。
-
-
基本情况:
-
如果
l == r,直接返回[1, 0](若s[l] == '0')或[0, 1](若s[l] == '1')。
-
-
递归情况:
-
遍历每个逻辑运算符
s[k](k为奇数位置):-
递归计算左子表达式
s[l...k-1]和右子表达式s[k+1...r]的结果[a, b]和[c, d]。 -
根据运算符
s[k]合并结果:-
AND (
&):-
0的方法数:a*c + a*d + b*c(任意一边为0)。 -
1的方法数:b*d(两边均为1)。
-
-
OR (
|):-
0的方法数:a*c(两边均为0)。 -
1的方法数:a*d + b*c + b*d(至少一边为1)。
-
-
XOR (
^):-
0的方法数:a*c + b*d(两边相同)。 -
1的方法数:a*d + b*c(两边不同)。
-
-
-
-
-
返回结果:
f(0, n-1)[result]。
-
- (2) 动态规划(Bottom-Up DP)
-
初始化:
-
对每个单字符
s[i],初始化dp[i][i]和dp[i][i]。
-
-
填表顺序:
-
按子表达式长度从小到大计算,确保
dp[l][r]依赖于已计算的dp[l][k-1]和dp[k+1][r]。
-
-
状态转移:
-
对于每个子表达式
s[l...r],枚举运算符s[k],合并左右子结果(逻辑同上)。
-
-
最终结果:
dp[n-1][result]。
-
- (1) 记忆化搜索(Top-Down DP)
-
复杂度分析
|
|
|
|---|---|---|
|
|
|
|
|
|
-
三重循环:外层
l、中层r、内层k,共 O(n³)。 -
空间优化:
dp表为 O(n²)(每个dp[l][r]存储两个值)。 -
示例
- 输入:
s = "1^0|0|1",result = 0 - 计算过程:
-
拆分
1 ^ (0 | (0 | 1)):-
0 | (0 | 1)→0 | 1→1。 -
1 ^ 1→0(方法数+1)。
-
-
拆分
(1 ^ 0) | (0 | 1):-
1 ^ 0→1。 -
0 | 1→1。 -
1 | 1→1(不满足)。
-
-
其他拆分方式均无法得到
0,最终结果为1种。
-
- 输入:
-
总结
-
核心思想:分治 + 动态规划,通过枚举最后计算的运算符将问题分解为子问题。
-
关键点:
-
状态定义:
dp[l][r][0/1]表示子表达式s[l...r]的结果分布。 -
状态转移:根据运算符性质合并左右子结果。
-
-
适用场景:表达式计算、括号添加问题(如矩阵链乘法)。
-
代码实现
// 布尔运算
// 给定一个布尔表达式和一个期望的布尔结果 result
// 布尔表达式由 0 (false)、1 (true)、& (AND)、 | (OR) 和 ^ (XOR) 符号组成
// 布尔表达式一定是正确的,不需要检查有效性
// 但是其中没有任何括号来表示优先级
// 你可以随意添加括号来改变逻辑优先级
// 目的是让表达式能够最终得出result的结果
// 返回最终得出result有多少种不同的逻辑计算顺序
// 测试链接 : https://leetcode.cn/problems/boolean-evaluation-lcci/
public class Code06_BooleanEvaluation {
// 记忆化搜索
public static int countEval(String str, int result) {
char[] s = str.toCharArray();
int n = s.length;
int[][][] dp = new int[n][n][];
int[] ft = f(s, 0, n - 1, dp);
return ft[result];
}
// s[l...r]是表达式的一部分,且一定符合范式
// 0/1 逻 0/1 逻 0/1
// l l+1 l+2 l+3........r
// s[l...r] 0 : ?
// 1 : ?
// ans : int[2] ans[0] = false方法数 ans[0] = true方法数
public static int[] f(char[] s, int l, int r, int[][][] dp) {
if (dp[l][r] != null) {
return dp[l][r];
}
int f = 0;
int t = 0;
if (l == r) {
// 只剩一个字符,0/1
f = s[l] == '0' ? 1 : 0;
t = s[l] == '1' ? 1 : 0;
} else {
int[] tmp;
for (int k = l + 1, a, b, c, d; k < r; k += 2) {
// l ... r
// 枚举每一个逻辑符号最后执行 k = l+1 ... r-1 k+=2
tmp = f(s, l, k - 1, dp);
a = tmp[0];
b = tmp[1];
tmp = f(s, k + 1, r, dp);
c = tmp[0];
d = tmp[1];
if (s[k] == '&') {
f += a * c + a * d + b * c;
t += b * d;
} else if (s[k] == '|') {
f += a * c;
t += a * d + b * c + b * d;
} else {
f += a * c + b * d;
t += a * d + b * c;
}
}
}
int[] ft = new int[] { f, t };
dp[l][r] = ft;
return ft;
}
}




















 996
996

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








