线性回归与高级回归模型实践:线性回归应用-优快云博客

学习内容

1 线性回归的建模与预测

线性回归是一种简单且常用的统计分析方法，核心目标是探索自变量与因变量之间的线性关联规律，并构建预测模型。它假设两个变量间存在一条近似直线的趋势，通过分析历史数据找到这条最贴合的“直线”，使数据点到直线的整体偏离程度最小。例如在房价预测中，房屋面积（自变量）与售价（因变量）可能存在线性关系，面积越大售价越高，线性回归能基于过往成交数据拟合出这条关系线，后续输入新房屋面积即可预测售价。

在实际应用中，线性回归可处理多变量问题，即分析多个因素对结果的综合影响。例如预测学生成绩时，自变量可包括学习时长、课外辅导次数、作业完成质量等，通过线性回归能找出各因素对成绩的影响权重，明确哪些因素对成绩提升更关键。此外，线性回归结果直观易懂，拟合出的直线或平面方程能清晰展示变量间的数学关系，便于后续分析和决策。不过，线性回归要求变量间存在线性关系，且对异常值敏感，若数据中存在极端值，可能使拟合结果偏离真实规律，使用时需结合数据特点合理应用。

1.1 环境准备

安装seaborn模块，导入Python中常用的数据分析和可视化库（NumPy、Pandas、Matplotlib、Seaborn），并设置Matplotlib图表直接在Jupyter Notebook中显示，为后续数据处理和可视化做准备。

%pip install seaborn
%pip install ipywidgets

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

1.2 下载数据集并读取

通过wget下载并解压包含美国房价数据的压缩包，读取CSV文件到Pandas DataFrame，并展示前5行数据以初步查看数据结构。

!wget https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_datasets/6f50105cd95411ef874afa163edcddae/USA_Housing.csv

df = pd.read_csv("USA_Housing.csv")
df.head()

1.3 检查数据集的基本信息

分别展示数据框的详细信息（包括列类型和非空值数量）、关键统计量（分位数从10%到90%）以及所有列名，用于快速了解数据集的结构、分布和特征。

info() 方法检查数据类型和数字

df.info(verbose=True)

describe() 方法获取数据集各种特征的统计摘要

df.describe(percentiles=[0.1,0.25,0.5,0.75,0.9])

columns 属性获取列（特征）的名称

df.columns

1.4 数据集的基本绘图和可视化

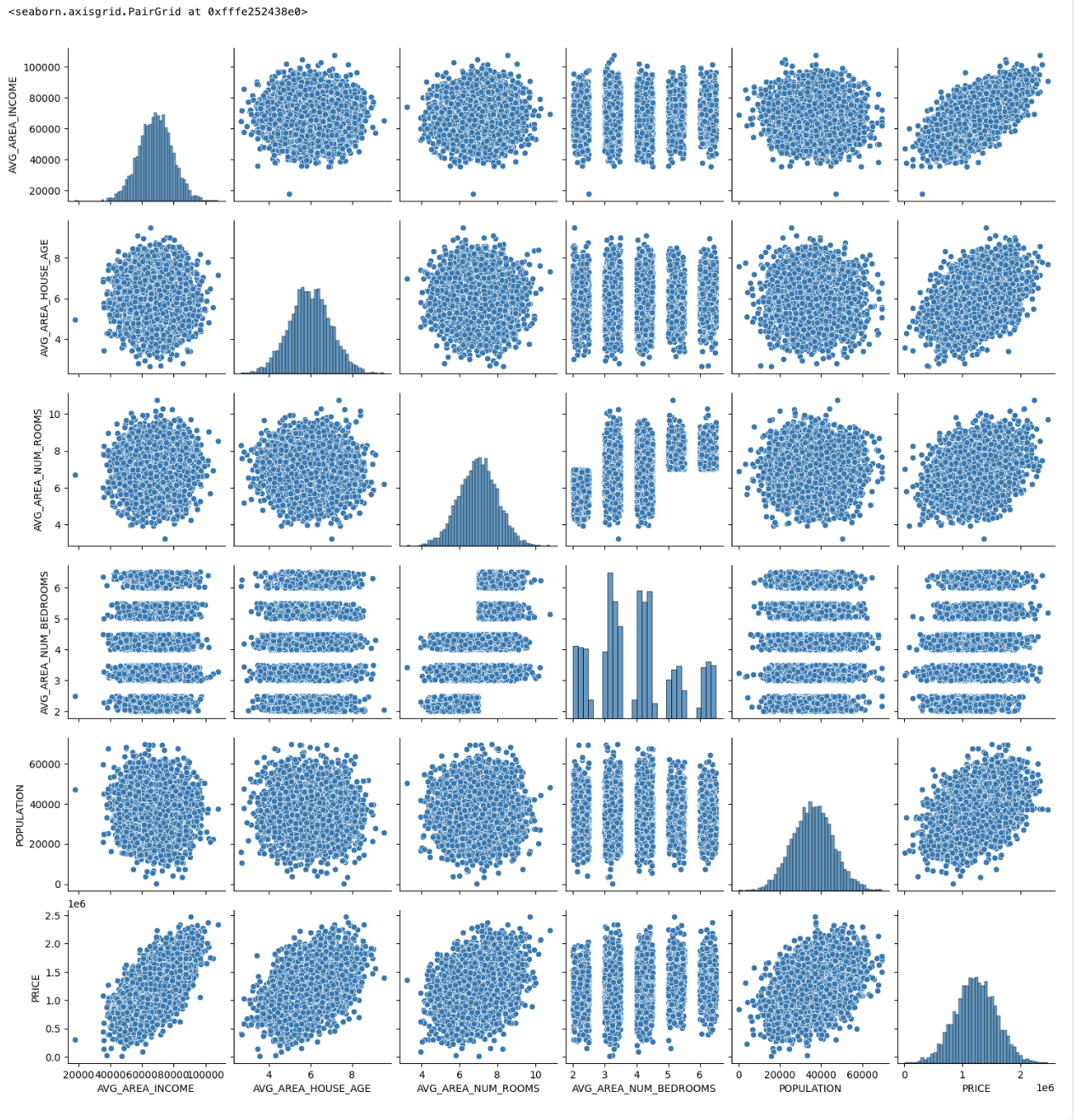
通过Seaborn的pairplot可视化各变量间关系，绘制房价直方图与密度图分析分布，计算并绘制相关系数热力图（含数值标注），以探索数据分布特征及变量相关性。
使用 seaborn 的 Pairplots

sns.pairplot(df)

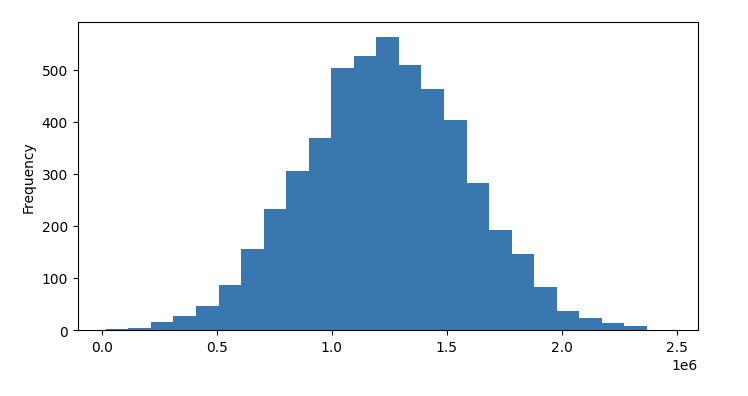
在这里插入图片描述
价格分布（预测数量）

df['PRICE'].plot.hist(bins=25,figsize=(8,4))

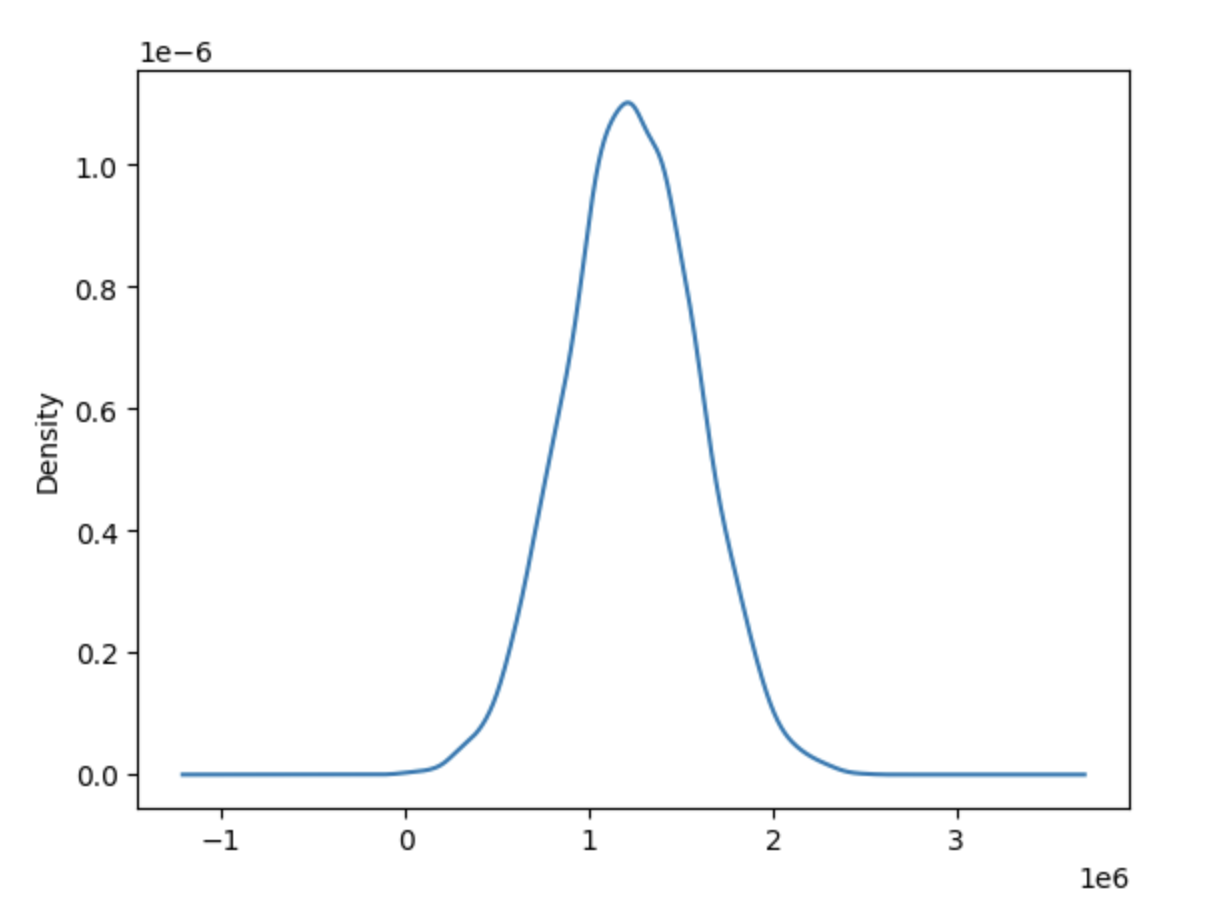
在这里插入图片描述

df['PRICE'].plot.density()

在这里插入图片描述
相关矩阵和热图展示

# 选择数值类型的列
numeric_df = df.select_dtypes(include=['float64', 'int64'])

# 计算相关系数矩阵
numeric_df.corr()

在这里插入图片描述

# 绘制热图
plt.figure(figsize=(10, 7))
sns.heatmap(numeric_df.corr(), annot=True, linewidths=2)

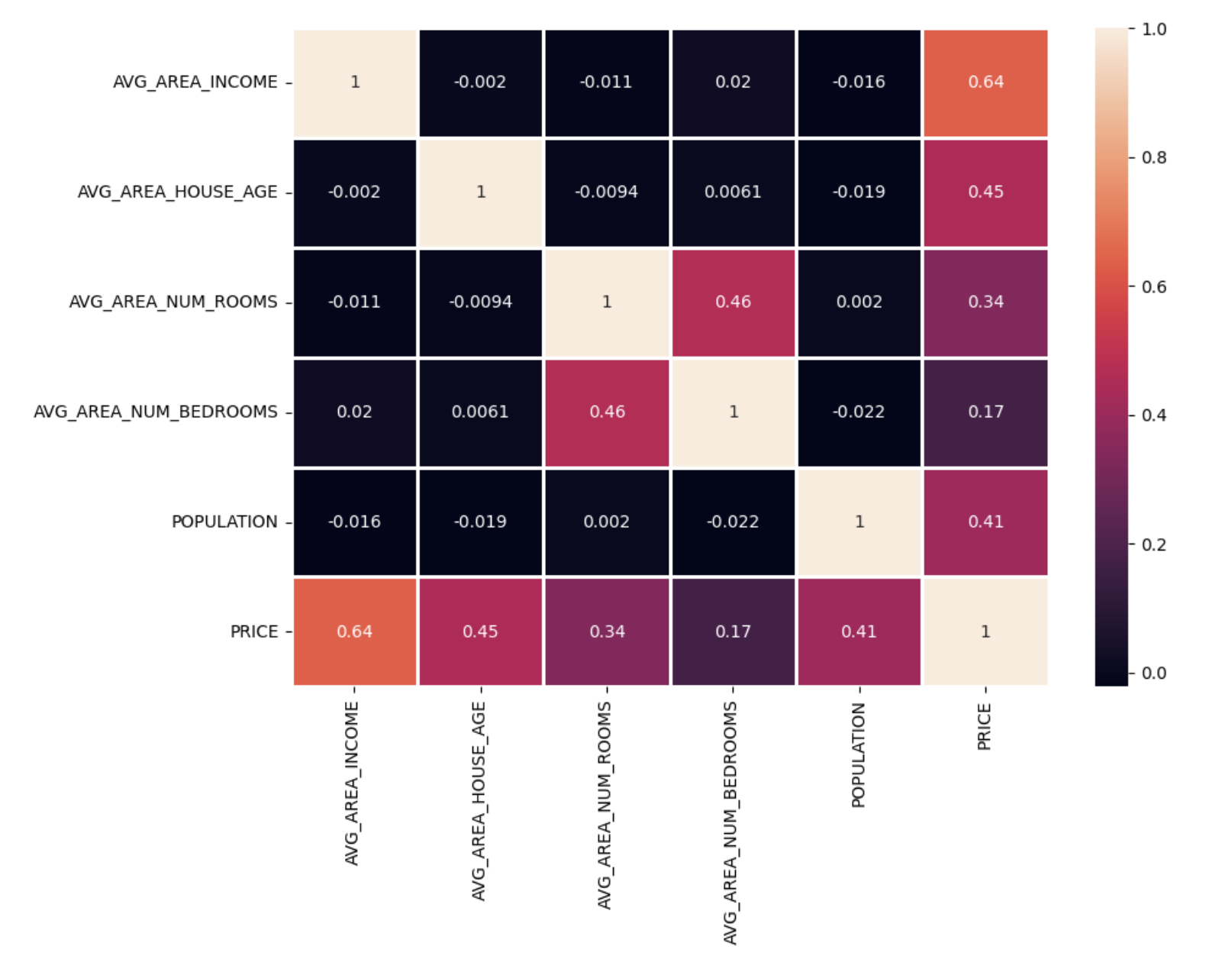
在这里插入图片描述

1.5 Feature 和变量集

提取数据框的列名列表，将前n-2列作为特征矩阵X，倒数第二列作为目标变量y，并打印它们的维度以确认数据分割正确。
创建数据框列名称列表

l_column = list(df.columns) # 列出列名
len_feature = len(l_column) # 列向量列表长度
l_column

将所有数值特征放在 X 中，将所有数字特征放在 y 中，忽略线性回归的字符串 Address

X = df[l_column[0:len_feature-2]]
y = df[l_column[len_feature-2]]

print("Feature set size:",X.shape)
print("Variable set size:",y.shape)

X.head()
y.head()

1.6 训练集与测试集的拆分

使用scikit-learn的train_test_split函数将特征矩阵X和目标变量y按7:3比例划分为训练集和测试集，设置随机种子123确保可重复性，并打印各数据集的维度以验证划分结果。
从 scikit-learn 导入 train_test_split 函数

from sklearn.model_selection import train_test_split

使用拆分比率和随机种子在一个命令中创建 X 和 y 训练和测试拆分

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=123)

检查训练/测试拆分的大小和形状（它应该在上述 test_size 参数的比率中）

print("Training feature set size:",X_train.shape)
print("Test feature set size:",X_test.shape)
print("Training variable set size:",y_train.shape)
print("Test variable set size:",y_test.shape)

1.7 对房价数据建模以及训练

使用scikit-learn的LinearRegression构建线性回归模型，在训练集上拟合后输出截距项和各特征的回归系数，并将系数整理为以特征名为索引的DataFrame，便于直观查看各变量对目标变量的影响程度。
从 scikit-learn 导入线性回归模型估计器并实例化

from sklearn.linear_model import LinearRegression
from sklearn import metrics
lm = LinearRegression() # 创建线性回归对象'lm'

将模型拟合到实例化对象本身

lm.fit(X_train,y_train) # 将线性模型拟合到“lm”对象本身上，即不需要将其设置为另一个变量

检查截距和系数并将它们放入 DataFrame 中

print("The intercept term of the linear model:", lm.intercept_)
print("The coefficients of the linear model:", lm.coef_)
cdf = pd.DataFrame(data=lm.coef_, index=X_train.columns, columns=["Coefficients"])
cdf

1.8 计算系数的标准误差和 t 统计量

计算线性回归模型中各特征系数的标准误和t统计量，评估特征重要性；按t统计量降序排列特征，输出重要性排序；最后绘制前四个重要特征与房价的散点图，直观展示它们与房价的线性关系。具体步骤包括：计算自由度、训练误差、标准误；构建包含系数、标准误和t统计量的DataFrame；按t统计量排序特征并输出；创建2x3的子图布局，分别绘制各特征与房价的散点图，并设置标题。

# 假设 lm 是一个线性回归模型，X_train 和 y_train 是训练数据
# 计算训练预测和误差
train_pred = lm.predict(X_train)
train_error = np.square(train_pred - y_train)
sum_error = np.sum(train_error)

# 计算自由度
dfN = X_train.shape[0] - X_train.shape[1]

# 初始化标准误差列表
k = X_train.shape[1]
se = [0] * k  # 初始化一个大小为 k 的列表

for i in range(k):
    r = (sum_error/dfN)
    r = r/np.sum(np.square(X_train[list(X_train.columns)[i]]-X_train[list(X_train.columns)[i]].mean()))
    se[i]=np.sqrt(r)
cdf['Standard Error']=se
cdf['t-statistic']=cdf['Coefficients']/cdf['Standard Error']
cdf

print("Therefore, features arranged in the order of importance for predicting the house price\n",'-'*90,sep='')
l=list(cdf.sort_values('t-statistic',ascending=False).index)
print(' > \n'.join(l))

l=list(cdf.index)
from matplotlib import gridspec
fig = plt.figure(figsize=(18, 10))
gs = gridspec.GridSpec(2,3)
#f, ax = plt.subplots(nrows=1,ncols=len(l), sharey=True)
ax0 = plt.subplot(gs[0])
ax0.scatter(df[l[0]],df['PRICE'])
ax0.set_title(l[0]+" vs. PRICE", fontdict={
   
   'fontsize':20})

ax1 = plt.subplot(gs[1])
ax1.scatter(df[l[1]],df['PRICE'])
ax1.set_title(l[1]+