线性回归与高级回归模型实践 ：不同方法实现线性回归

使用不同方法实现线性回归

学习目标

通过本课程可以了解到如何使用多种工具以及多种方法进行简单的线性回归的展示。

相关知识点

• 不同方法线性回归实现

学习内容

1 不同方法线性回归实现

不同方法

• Numpy.Polyfit：通过最小二乘法拟合任意阶多项式曲线以近似线性或非线性关系，适用于快速建模数据趋势，但需手动调整阶数平衡拟合精度与过拟合风险，本质为多项式展开的线性回归变体。

• Stats.linregress：针对单变量线性回归场景，直接计算斜率、截距、相关系数及显著性p值，提供基础统计诊断，适合快速验证两个变量的线性关联强度，但无法处理多变量或非线性问题。

• Optimize.curve_fit：通过最小化残差平方和拟合用户自定义函数到数据，支持非线性回归任务，需显式定义函数形式，适用于科学计算中需灵活建模复杂关系的场景。

• Numpy.linalg.lstsq：以矩阵形式求解线性最小二乘问题，返回超定或欠定方程组的最优解，支持多变量线性回归的数值实现，但缺乏正则化机制，对特征共线性或病态矩阵敏感，常用于底层数值计算或教学演示。

• Statsmodels.OLS：实现经典普通最小二乘回归，提供完整统计检验、模型诊断及假设验证，适合学术研究或严格统计推断，但需手动处理常数项且计算效率较低。

• Moore-Penrose：通过奇异值分解计算矩阵伪逆，求解病态或欠定方程组的最小范数解，适用于特征数远超样本数的高维场景（如基因组学、信号处理），通过正则化隐式处理共线性，但计算复杂度较高且缺乏统计解释性。

• Simple inverse：基于可逆矩阵的逆 $A^{-}1$求解线性方程组 $A_x=b$，仅适用于理论上的方阵且行列式非零场景，计算简单但数值稳定性差，易受噪声干扰，实际工程中已被广义逆或分解方法替代。

• Sklearn.linear_model:提供线性回归及正则化变体，支持大规模数据、交叉验证、网格调参与模型集成，适合机器学习流水线中的高效建模与部署。

1.1 环境准备

pip install statsmodels

导入了多个Python科学计算和数据分析库（如SciPy、NumPy、StatsModels、Matplotlib、Scikit-learn和Pandas），用于后续的统计分析、线性回归建模、数据可视化及交互式绘图。

from scipy import stats, optimize
from numpy import polyfit,sqrt ,polyval
import statsmodels.api as sm
import matplotlib.pyplot as plt
import time
import numpy as np
from sklearn.linear_model import LinearRegression
import pandas as pd
#确保图表内嵌显示
%matplotlib inline

1.2 使用numpy生成足够大的随机数据

生成一个包含500万个数据点的线性数据集，其中自变量t均匀分布在[-10,10]区间，因变量x由线性方程𝑥=3.25𝑡−6.5生成，并添加了标准差为3的高斯噪声（xn=x+3*np.random.randn(n)），最终得到含噪声的观测值xn。

#创建示例数据
#数据点 
n=int(5e6)
t=np.linspace(-10,10,n)
#数据的范围
a=3.25; b=-6.5
x=np.polyval([a,b],t)
#添加一些噪声
xn=x+3*np.random.randn(n)

1.3 绘制几个随机采样点并绘图

从均匀分布的自变量t中随机抽取20个点作为样本，计算其对应的线性关系值（𝑦=3.25𝑥−6.5）并添加高斯噪声，最终通过绿色散点图（带黑色边缘）可视化这些样本点，并启用网格线辅助观察数据分布。

xvar=np.random.choice(t,size=20)
yvar=polyval([a,b],xvar)+3*np.random.randn(20)
plt.scatter(xvar,yvar,c='green',edgecolors='k')
plt.grid(True)
plt.show()

1.4 多种方法的线性回归

Numpy.Polyfit 的方法

使用NumPy的polyfit函数对含噪声的线性数据（t与xn）进行一阶多项式拟合（即线性回归），计算拟合参数（斜率ar和截距br）、均方根误差（RMSE），并输出拟合结果、误差及计算耗时，展示了如何通过最小二乘法快速实现线性模型拟合与评估。

#线性回归-多元拟合-多元拟合可用于其他阶多项式
t1=time.time()
(ar,br)=polyfit(t,xn,1)
xr=polyval([ar,br],t)
#计算均方误差
err=sqrt(sum((xr-xn)**2)/n)
t2=time.time()
t_polyfit = float(t2-t1)

print('Linear regression using polyfit')
print('parameters: a=%.2f b=%.2f, ms error= %.3f' % (ar,br,err))
print("Time taken: {} seconds".format(t_polyfit))

Stats.linregress 的方法

使用SciPy的stats.linregress函数对数据（t与xn）进行线性回归，输出斜率（a_s）、截距（b_s）、标准误差（stderr）、相关系数（r）及计算耗时，展示了通过统计方法快速获取回归参数与模型评估指标的实现方式。

#使用 stats.linregress 进行线性回归
t1=time.time()
(a_s,b_s,r,tt,stderr)=stats.linregress(t,xn)
t2=time.time()
t_linregress = float(t2-t1)

print('Linear regression using stats.linregress')
print('a=%.2f b=%.2f, std error= %.3f, r^2 coefficient= %.3f' % (a_s,b_s,stderr,r))
print("Time taken: {} seconds".format(t_linregress))

Optimize.curve_fit 的方法

使用SciPy的optimize.curve_fit函数，通过非线性最小二乘法对自定义线性模型flin(t,a,b)=a*t+b进行参数拟合（a和b），输出拟合结果及计算耗时，展示了通过优化框架实现灵活模型拟合的方法。

def flin(t,a,b):
    result = a*t+b
    return(result)

t1=time.time()
p1,_=optimize.curve_fit(flin,xdata=t,ydata=xn,method='lm')
t2=time.time()
t_optimize_curve_fit = float(t2-t1)

print('Linear regression using optimize.curve_fit')
print('parameters: a=%.2f b=%.2f' % (p1[0],p1[1]))
print("Time taken: {} seconds".format(t_optimize_curve_fit))

numpy.linalg.lstsq 的方法

使用numpy.linalg.lstsq进行线性回归，计算斜率和截距参数（ar和br）及均方根误差（err），并输出执行时间（秒）和参数结果。

t1=time.time()
A = np.vstack([t, np.ones(len(t))]).T
result = np.linalg.lstsq(A, xn, rcond=-1)
ar,br = result[0]
err = np.sqrt(result[1]/len(xn))
t2=time.time()
t_linalg_lstsq = float(t2-t1)

print('Linear regression using numpy.linalg.lstsq')
print('parameters: a=%.2f b=%.2f, ms error= %.3f' % (ar,br,err))
print("Time taken: {} seconds".format(t_linalg_lstsq))

Statsmodels.OLS 的方法

使用StatsModels库的OLS（普通最小二乘法）对添加了常数项的自变量t（通过sm.add_constant）和因变量x进行线性回归，输出拟合参数（斜率ar和截距br）、计算耗时及详细的统计摘要（results.summary()），展示了通过统计建模框架实现回归分析并获取完整诊断信息的方法。

t1=time.time()
t=sm.add_constant(t)
model = sm.OLS(x, t)
results = model.fit()
ar=results.params[1]
br=results.params[0]
t2=time.time()
t_OLS = float(t2-t1)

print('Linear regression using statsmodels.OLS')
print('parameters: a=%.2f b=%.2f'% (ar,br))
print("Time taken: {} seconds".format(t_OLS))   
print(results.summary())

Moore-Penrose 伪逆的解析解的方法

通过NumPy计算自变量矩阵t的Moore-Penrose伪逆（np.linalg.pinv），并用其直接求解线性回归参数（斜率ar和截距br），输出结果及计算耗时，展示了利用矩阵伪逆实现闭式解的最小二乘估计方法

t1=time.time()
mpinv = np.linalg.pinv(t)
result = mpinv.dot(x)
ar = result[1]
br = result[0]
t2=time.time()
t_inv_matrix = float(t2-t1)

print('Linear regression using Moore-Penrose inverse')
print('parameters: a=%.2f b=%.2f'% (ar,br))
print("Time taken: {} seconds".format(t_inv_matrix)) 

使用简单乘法矩阵逆的解析解的方法

通过手动计算正规方程（𝑋ᵀ𝑋)⁻¹𝑋ᵀ𝑌）的解析解来求解线性回归参数（斜率ar和截距br），输出结果及计算耗时，展示了直接利用矩阵运算实现最小二乘估计的数学原理。

t1=time.time()
m = np.dot((np.dot(np.linalg.inv(np.dot(t.T,t)),t.T)),x)
ar = m[1]
br = m[0]
t2=time.time()
t_simple_inv = float(t2-t1)

print('Linear regression using simple inverse')
print('parameters: a=%.2f b=%.2f'% (ar,br))
print("Time taken: {} seconds".format(t_simple_inv)) 

sklearn.linear_model线性回归的方法

使用Scikit-learn的LinearRegression模型对数据（t与x）进行线性回归拟合，输出斜率（ar）和截距（br）参数及计算耗时，展示了通过机器学习库快速实现线性回归的标准方法。

t1=time.time()
lm = LinearRegression()
lm.fit(t,x)
ar=lm.coef_[1]
br=lm.intercept_
t2=time.time()
t_sklearn_linear = float(t2-t1)

print('Linear regression using sklearn.linear_model.LinearRegression')
print('parameters: a=%.2f b=%.2f'% (ar,br))
print("Time taken: {} seconds".format(t_sklearn_linear)) 

将所有方法的执行时间存入列表

将不同线性回归方法（polyfit、linregress、curve_fit、lstsq、OLS、伪逆、正规方程、Scikit-learn）的计算耗时存储到列表times中，便于后续比较各方法的执行效率。

times = [t_polyfit,t_linregress,t_optimize_curve_fit,t_linalg_lstsq,t_OLS,t_inv_matrix,t_simple_inv,t_sklearn_linear]

将执行时间以条形图展示

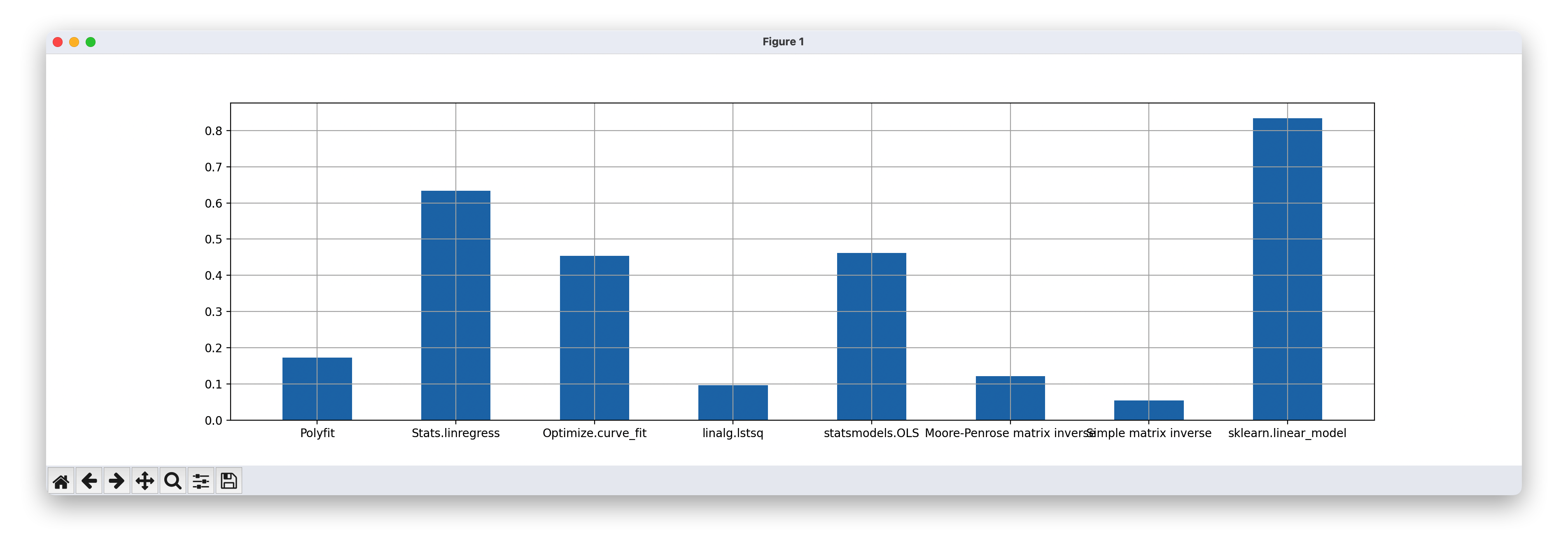
使用Matplotlib绘制了一个宽度为20英寸、高度为5英寸的条形图，展示不同线性回归方法（polyfit、linregress、curve_fit、lstsq、OLS、伪逆、正规方程、Scikit-learn）的计算耗时对比，启用了网格线（grid=True），并通过调整条形位置（x=[l*0.8 for l in range(8)]）和宽度（width=0.4）避免标签重叠，横轴标签清晰标注了每种方法名称。

plt.figure(figsize=(20,5))
plt.grid(True)
plt.bar(x=[l*0.8 for l in range(8)],height=times, width=0.4,
        tick_label=['Polyfit','Stats.linregress','Optimize.curve_fit',
                    'numpy.linalg.lstsq','statsmodels.OLS','Moore-Penrose matrix inverse',
                    'Simple matrix inverse','sklearn.linear_model'])
plt.show()

1.5 验证不同方法的执行时间

生成数据集

生成一个从50,000到10,000,000的对数均匀分布的整数列表（n_data），共25个点，用于后续分析或绘图时覆盖不同数据规模。

n_min = 50000
n_max = int(1e7)
n_levels = 25
r = np.log10(n_max/n_min)
l = np.linspace(0,r,n_levels)
n_data = list((n_min*np.power(10,l)))
n_data = [int(n) for n in n_data]

得出每个方法执行的时间

通过循环测试不同数据规模（从50,000到10,000,000，共25个对数间隔点）下8种线性回归方法（polyfit、linregress、curve_fit、lstsq、OLS、伪逆、正规方程、Scikit-learn）的执行时间（毫秒级），并将结果存储在字典time_dict中，使用tqdm显示进度条，模拟线性数据（y=3.25x-6.5+噪声）以评估各方法在不同数据量下的性能表现。

l1=['Polyfit', 'Stats.lingress','Optimize.curve_fit', 'linalg.lstsq', 
 'statsmodels.OLS', 'Moore-Penrose matrix inverse', 'Simple matrix inverse', 'sklearn.linear_model']
time_dict = {key:[] for key in l1}

from tqdm import tqdm

for i in tqdm(range(len(n_data))):
    t=np.linspace(-10,10,n_data[i])
    #parameters
    a=3.25; b=-6.5
    x=polyval([a,b],t)
    #add some noise
    xn=x+3*np.random.randn(n_data[i])
    
    #线性回归-多元拟合-多元拟合可用于其他阶多项式
    t1=time.time()
    (ar,br)=polyfit(t,xn,1)
    t2=time.time()
    t_polyfit = 1e3*float(t2-t1)
    time_dict['Polyfit'].append(t_polyfit)
    
    #使用stats.linregress进行线性回归
    t1=time.time()
    (a_s,b_s,r,tt,stderr)=stats.linregress(t,xn)
    t2=time.time()
    t_linregress = 1e3*float(t2-t1)
    time_dict['Stats.lingress'].append(t_linregress)
    
    #使用 optimize.curve_fit 进行线性回归
    t1=time.time()
    p1,_=optimize.curve_fit(flin,xdata=t,ydata=xn,method='lm')
    t2=time.time()
    t_optimize_curve_fit = 1e3*float(t2-t1)
    time_dict['Optimize.curve_fit'].append(t_optimize_curve_fit)
    
    # 使用 np.linalg.lstsq（求解 Ax=B 方程组）进行线性回归
    t1=time.time()
    A = np.vstack([t, np.ones(len(t))]).T
    result = np.linalg.lstsq(A, xn)
    ar,br = result[0]
    t2=time.time()
    t_linalg_lstsq = 1e3*float(t2-t1)
    time_dict['linalg.lstsq'].append(t_linalg_lstsq)
    
    # 使用 statsmodels.OLS 进行线性回归
    t1=time.time()
    t=sm.add_constant(t)
    model = sm.OLS(x, t)
    results = model.fit()
    ar=results.params[1]
    br=results.params[0]
    t2=time.time()
    t_OLS = 1e3*float(t2-t1)
    time_dict['statsmodels.OLS'].append(t_OLS)
    
    # 使用摩尔-彭罗斯（Moore-Penrose）伪逆矩阵进行线性回归
    t1=time.time()
    mpinv = np.linalg.pinv(t)
    result = mpinv.dot(x)
    ar = result[1]
    br = result[0]
    t2=time.time()
    t_mpinverse = 1e3*float(t2-t1)
    time_dict['Moore-Penrose matrix inverse'].append(t_mpinverse)
    
    # 使用简单乘法逆矩阵进行线性回归
    t1=time.time()
    m = np.dot((np.dot(np.linalg.inv(np.dot(t.T,t)),t.T)),x)
    ar = m[1]
    br = m[0]
    t2=time.time()
    t_simple_inv = 1e3*float(t2-t1)
    time_dict['Simple matrix inverse'].append(t_simple_inv)
    
    # 使用 scikit-learn 的 linear_model 进行线性回归
    t1=time.time()
    lm = LinearRegression()
    lm.fit(t,x)
    ar=lm.coef_[1]
    br=lm.intercept_
    t2=time.time()
    t_sklearn_linear = 1e3*float(t2-t1)
    time_dict['sklearn.linear_model'].append(t_sklearn_linear)

将存储不同线性回归方法执行时间的字典time_dict转换为Pandas的DataFrame对象df，便于后续进行数据分析和可视化操作。

df = pd.DataFrame(data=time_dict)
df

将执行时间以折线图展示

使用Matplotlib绘制一个对数坐标的折线图，横轴为数据集规模（样本数，范围从10⁵到10⁷），纵轴为各线性回归方法的执行时间（毫秒），通过semilogx实现对数刻度，设置了自定义的刻度标签和字体大小，启用了网格线（grid=True），并添加了图例（字体大小20），清晰展示了不同方法在不同数据量下的性能差异。

plt.figure(figsize=(15,10))
for i in df.columns:
    plt.semilogx((n_data),df[i],lw=3)
plt.xticks([1e5,2e5,5e5,1e6,2e6,5e6,1e7],fontsize=15)
plt.xlabel("\nSize of the data set (number of samples)",fontsize=15)
plt.yticks(fontsize=15)
plt.ylabel("Milliseconds needed for simple linear regression model fit\n",fontsize=15)
plt.grid(True)
plt.legend([name for name in df.columns],fontsize=20)

将执行时间以柱状图展示

绘制一个宽度为20英寸、高度为5英寸的条形图，展示在最大数据规模（10,000,000样本）下，8种线性回归方法的执行时间对比，启用了网格线，并通过调整条形位置和宽度避免标签重叠，横轴标签清晰标注了每种方法名称。

# 获取最后一行
a1=df.iloc[-1]
plt.figure(figsize=(20,5))
plt.grid(True)
plt.bar(x=[l*0.8 for l in range(8)],height=a1, width=0.4,
        tick_label=list(a1.index))
plt.show()