聚类算法实战:使用Scikit-learn探索数据的隐藏模式
学习目标
通过本课程的学习,学员将掌握Scikit-learn中聚类算法的基本原理和应用方法,包括K均值聚类和层次聚类。学员将能够使用这些算法对数据进行分组,发现数据中的模式,并能够评估聚类结果的质量。
相关知识点
- Scikit-learn聚类算法
学习内容
1 Scikit-learn聚类算法
1.1 K均值聚类
K均值聚类是一种无监督学习方法,用于将数据集划分为K个不同的簇。每个簇由其质心(即簇中所有点的平均位置)表示。算法的目标是使每个簇内的数据点尽可能相似,而不同簇之间的数据点尽可能不同。K均值聚类的基本步骤包括:
- 选择K个初始质心。
- 将每个数据点分配给最近的质心。
- 重新计算每个簇的质心。
- 重复上述步骤,直到质心不再变化或达到最大迭代次数。
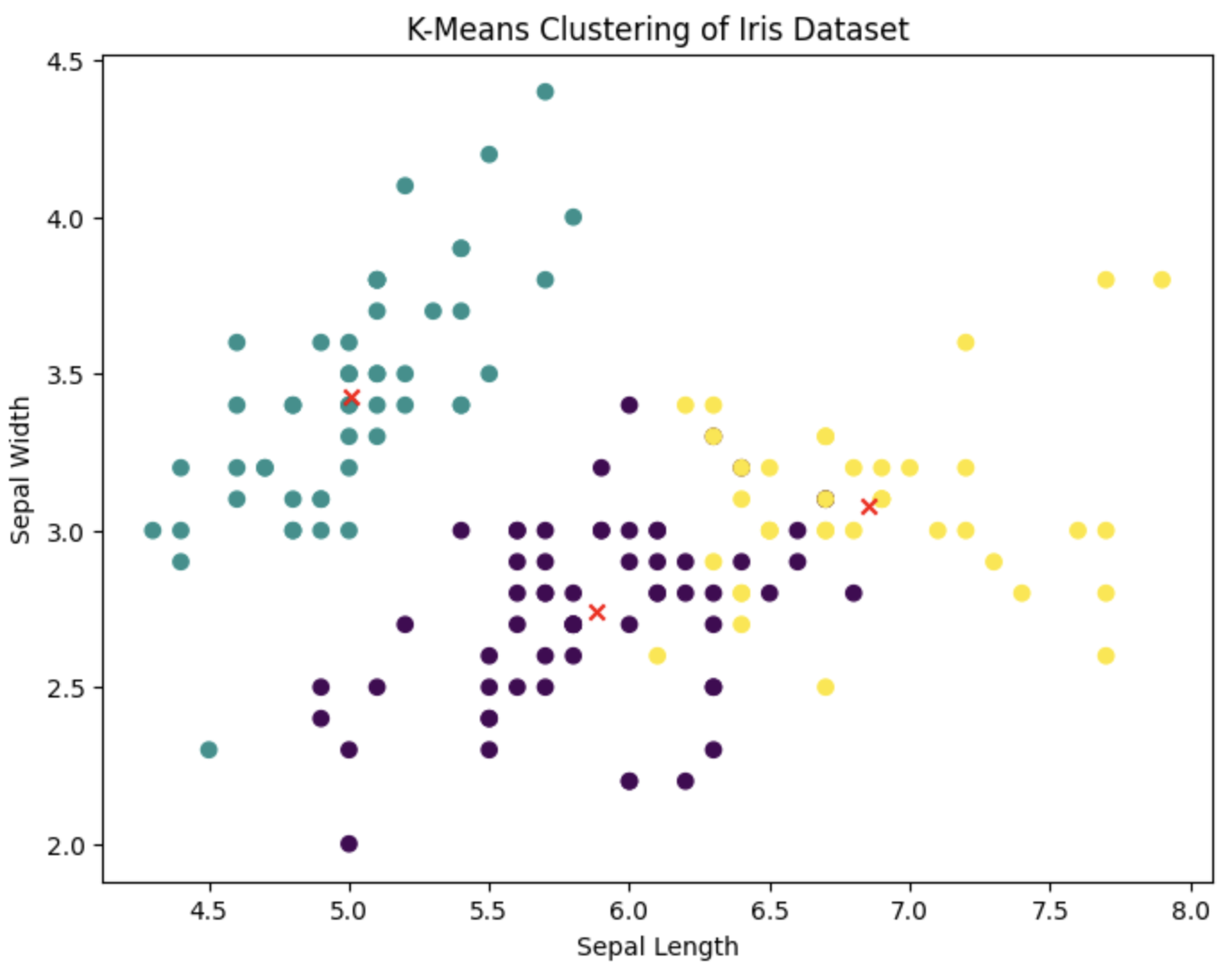
实践:使用K均值聚类分析鸢尾花数据集
首先,我们需要导入必要的库,并加载鸢尾花数据集。鸢尾花数据集是一个经典的数据集,包含150个样本,每个样本有4个特征,分别代表鸢尾花的萼片长度、萼片宽度、花瓣长度和花瓣宽度。
%pip install scikit-learn
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
# 加载数据
iris = load_iris()
X = iris.data
# 创建K均值聚类模型
kmeans = KMeans(n_clusters=3, random_state=0)
kmeans.fit(X)
# 获取聚类结果
labels = kmeans.labels_
centroids = kmeans.cluster_centers_
# 可视化聚类结果
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', marker='o')
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='x')
plt.title('K-Means Clustering of Iris Dataset')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.show()
1.2 层次聚类
层次聚类是一种基于树状图(树形结构)的聚类方法,可以分为凝聚层次聚类和分裂层次聚类。凝聚层次聚类从每个数据点作为一个单独的簇开始,然后逐步合并最近的簇,直到所有数据点合并为一个簇。分裂层次聚类则相反,从所有数据点作为一个簇开始,逐步分裂成更小的簇。
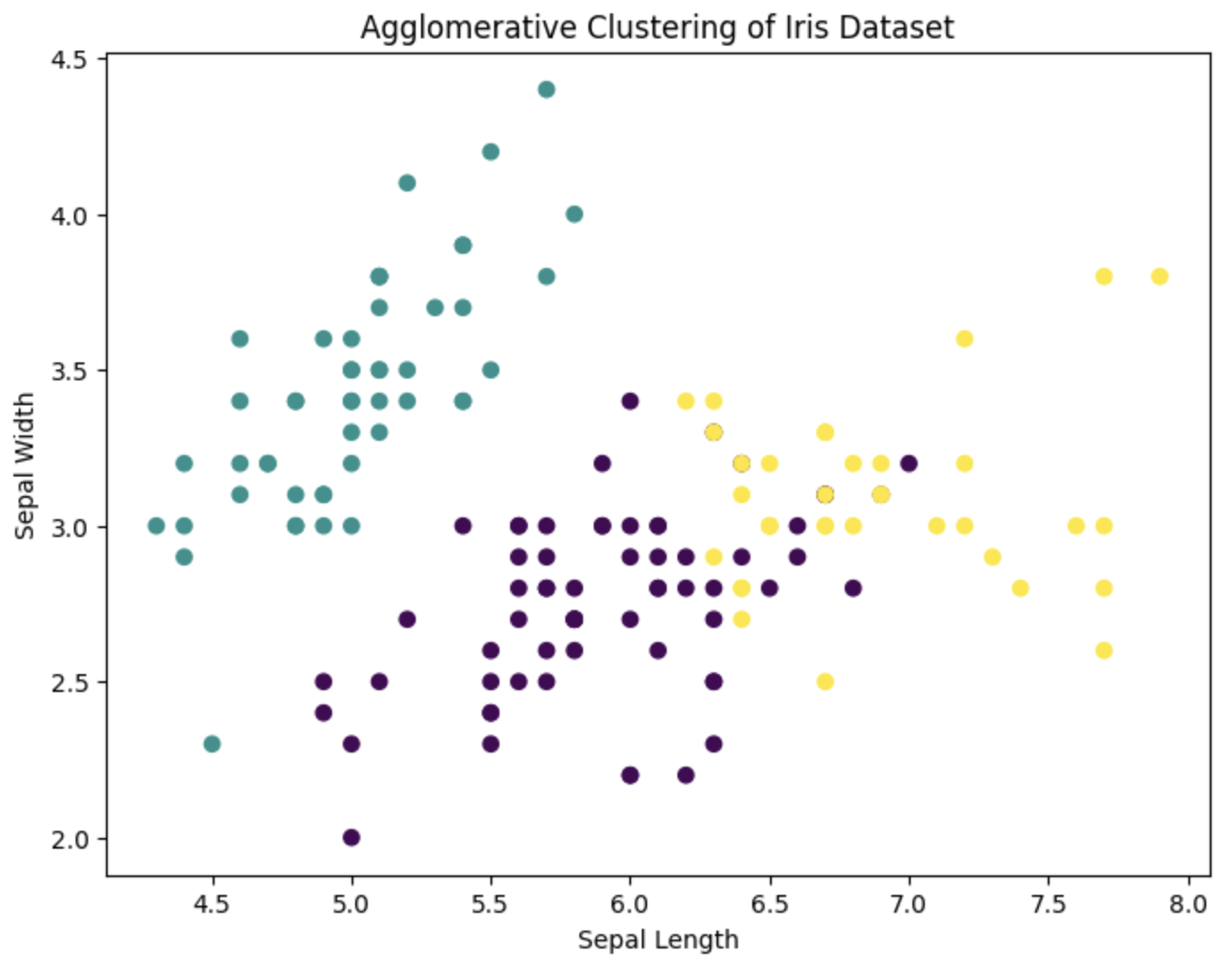
实践:使用凝聚层次聚类分析鸢尾花数据集
我们将使用Scikit-learn中的AgglomerativeClustering类来实现凝聚层次聚类。
from sklearn.cluster import AgglomerativeClustering
import scipy.cluster.hierarchy as shc
# 创建凝聚层次聚类模型
agg_clustering = AgglomerativeClustering(n_clusters=3)
agg_labels = agg_clustering.fit_predict(X)
# 可视化聚类结果
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=agg_labels, cmap='viridis', marker='o')
plt.title('Agglomerative Clustering of Iris Dataset')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.show()
1.3 聚类性能评估
评估聚类算法的性能是聚类分析中的重要步骤。常用的评估指标包括轮廓系数(Silhouette Coefficient)和Calinski-Harabasz指数。轮廓系数衡量了每个数据点与其所在簇的相似度与与其他簇的不相似度的差异。Calinski-Harabasz指数则通过簇内距离和簇间距离的比值来评估聚类效果。
实践:评估K均值聚类和层次聚类的性能
我们将使用轮廓系数和Calinski-Harabasz指数来评估K均值聚类和层次聚类的性能。
from sklearn.metrics import silhouette_score, calinski_harabasz_score
# 计算K均值聚类的性能指标
kmeans_silhouette = silhouette_score(X, labels)
kmeans_calinski_harabasz = calinski_harabasz_score(X, labels)
# 计算层次聚类的性能指标
agg_silhouette = silhouette_score(X, agg_labels)
agg_calinski_harabasz = calinski_harabasz_score(X, agg_labels)
print(f'K-Means Silhouette Score: {kmeans_silhouette}')
print(f'K-Means Calinski-Harabasz Score: {kmeans_calinski_harabasz}')
print(f'Agglomerative Clustering Silhouette Score: {agg_silhouette}')
print(f'Agglomerative Clustering Calinski-Harabasz Score: {agg_calinski_harabasz}')
K-Means Silhouette Score: 0.5511916046195919
K-Means Calinski-Harabasz Score: 561.593732015664
Agglomerative Clustering Silhouette Score: 0.5543236611296419
Agglomerative Clustering Calinski-Harabasz Score: 558.0580408128307
通过上述实践,学员将能够熟练掌握K均值聚类和层次聚类的基本原理和应用方法,并能够评估聚类结果的质量。
评估参数详解:
这段代码用于评估两种聚类算法(K-Means聚类和层次聚类)的性能,并通过两种常用指标对比它们的聚类效果。以下是详细解释:
1. 代码功能概述
- 从
sklearn.metrics导入了两个聚类评估指标:silhouette_score(轮廓系数)和calinski_harabasz_score(Calinski-Harabasz指数)。 - 分别计算了K-Means聚类和层次聚类(Agglomerative Clustering) 的这两个指标。
- 打印输出两种算法的指标结果,用于对比聚类效果。
2. 核心概念与指标解释
输入参数说明
X:原始数据集(特征矩阵),即被聚类的样本数据。labels/agg_labels:聚类算法输出的标签(每个样本被分配到的簇编号),其中labels对应K-Means的结果,agg_labels对应层次聚类的结果。
(1)Silhouette Score(轮廓系数)
- 含义:衡量聚类结果的“紧密性”和“分离度”,评估样本与其所属簇的相似度以及与其他簇的差异度。
- 取值范围:-1 ~ 1
- 接近1:样本与自身簇高度相似,与其他簇差异大(聚类效果好)。
- 接近0:样本处于两个簇的边界附近(聚类模糊)。
- 接近-1:样本可能被分配到错误的簇(聚类效果差)。
- 结果分析:
- K-Means的轮廓系数为
0.551,层次聚类为0.554,两者非常接近且均大于0.5,说明两种算法的聚类结果整体合理,样本在簇内的相似度高于与其他簇的相似度。
- K-Means的轮廓系数为
(2)Calinski-Harabasz Score(Calinski-Harabasz指数,也称为方差比标准)
- 含义:通过计算“簇间离散度”与“簇内离散度”的比值来评估聚类效果。
- 簇间离散度:不同簇之间的差异(越大越好)。
- 簇内离散度:同一簇内样本的差异(越小越好)。
因此,该指数数值越大,说明聚类效果越好(簇内越紧凑,簇间越分散)。
- 结果分析:
- K-Means的指数为
561.59,层次聚类为558.06,两者数值接近且均较大,进一步说明两种算法都实现了较好的聚类分离。
- K-Means的指数为
3. 两种算法的对比结论
从输出结果来看:
- 层次聚类的轮廓系数略高(0.554 > 0.551),说明其在样本“簇内相似度”和“簇间差异度”的平衡上稍好。
- K-Means的Calinski-Harabasz指数略高(561.59 > 558.06),说明其在“簇间分散”和“簇内紧凑”的整体表现上稍优。
总体而言,两种聚类算法的性能非常接近,均达到了中等偏上的聚类效果(轮廓系数>0.5,Calinski-Harabasz指数较大)。在实际应用中,可能需要结合具体业务场景(如算法效率、可解释性等)进一步选择。




















 804
804

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








