降维技术:探索数据的多维世界
学习目标
通过本课程的学习,学员将掌握降维技术的基本概念,了解如何使用Scikit-learn库中的PCA(主成分分析)和t-SNE(t分布随机邻域嵌入)方法进行数据降维。实验将通过理论讲解与实践操作相结合的方式,帮助学员深入理解降维技术在数据分析中的应用。
相关知识点
- Scikit-learn降维技术
学习内容
1 Scikit-learn降维技术
1.1 主成分分析(PCA)
主成分分析(Principal Component Analysis, PCA)是一种统计方法,通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量称为主成分。PCA的主要目的是减少数据集的维度,同时保留尽可能多的原始数据信息。在数据预处理、特征提取和数据可视化等领域,PCA有着广泛的应用。
理论基础
PCA的核心思想是通过找到数据的主成分方向,即数据方差最大的方向,来实现数据的降维。具体步骤如下:
- 数据标准化:由于PCA对数据的尺度敏感,因此在进行PCA之前,通常需要对数据进行标准化处理,使每个特征的均值为0,方差为1。
- 计算协方差矩阵:协方差矩阵描述了数据集中各特征之间的线性关系。对于一个n维数据集,协方差矩阵是一个n×n的对称矩阵。
- 计算特征值和特征向量:通过计算协方差矩阵的特征值和特征向量,可以找到数据的主要方向。特征值表示数据在该方向上的方差,特征向量表示数据的主要方向。
- 选择主成分:根据特征值的大小,选择前k个特征向量作为主成分,k通常小于原始数据的维度。
- 数据投影:将原始数据投影到选定的主成分方向上,得到降维后的数据。
实践操作
下面我们将使用Scikit-learn库中的PCA类来实现数据降维。我们将使用Iris数据集作为示例。
%pip install scikit-learn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
# 加载Iris数据集
iris = load_iris()
X = iris.data
y = iris.target
# 数据标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 应用PCA
pca = PCA(n_components=2) # 选择降维后的维度为2
X_pca = pca.fit_transform(X_scaled)
# 可视化降维后的数据
plt.figure(figsize=(8, 6))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis', edgecolor='k', s=80)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA of Iris Dataset')
plt.show()
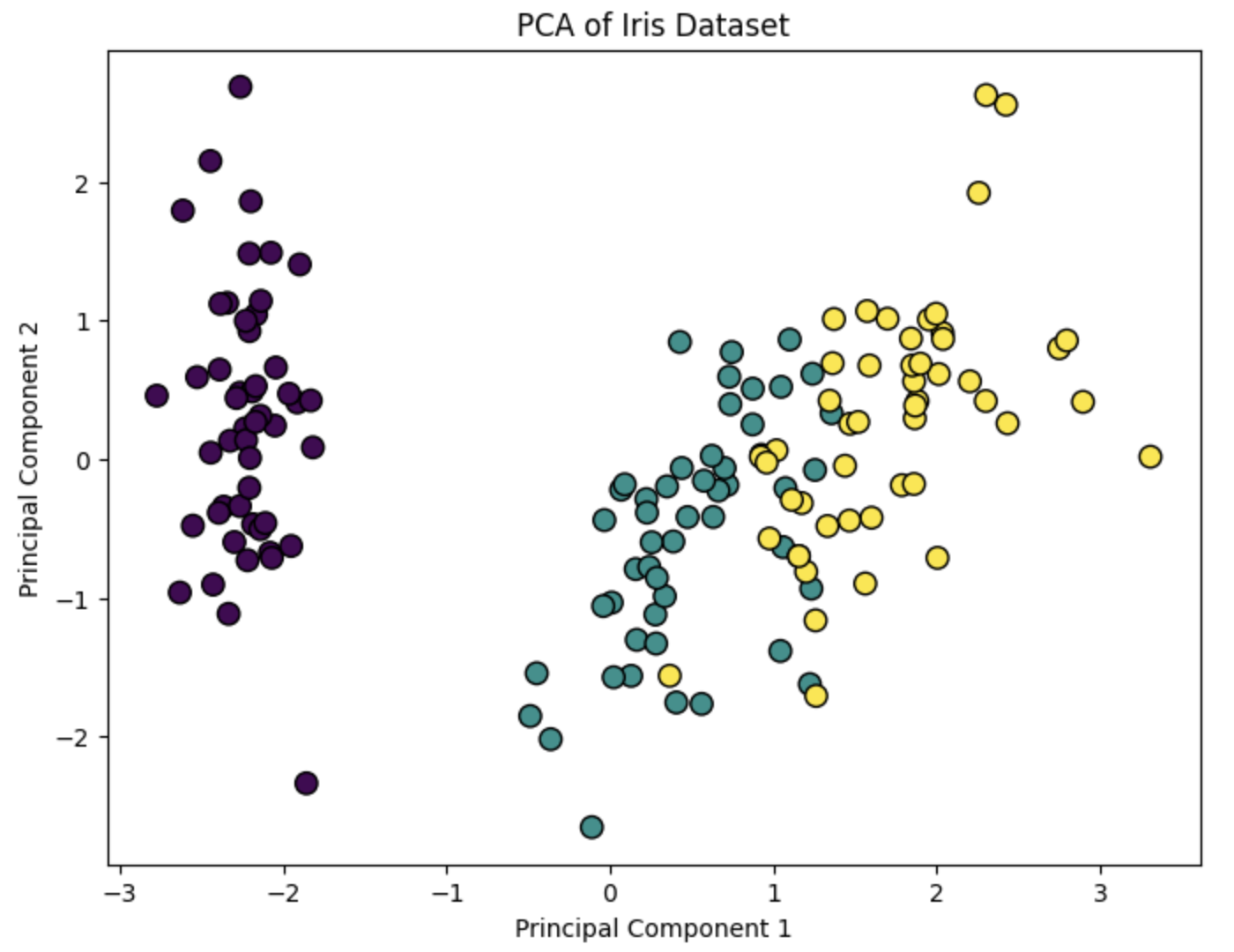
1.2 t分布随机邻域嵌入(t-SNE)
t分布随机邻域嵌入(t-Distributed Stochastic Neighbor Embedding, t-SNE)是一种非线性的降维方法,特别适用于高维数据的可视化。t-SNE通过在高维空间中计算数据点之间的相似度,并在低维空间中保持这些相似度,从而实现数据的降维。与PCA不同,t-SNE更关注数据点之间的局部结构,因此在可视化高维数据时效果更好。
理论基础
t-SNE的主要步骤如下:
- 计算高维空间中的相似度:t-SNE首先在高维空间中计算数据点之间的相似度,通常使用高斯分布来计算。
- 计算低维空间中的相似度:在低维空间中,t-SNE使用t分布来计算数据点之间的相似度。
- 优化目标函数:t-SNE通过最小化高维空间和低维空间中相似度的差异来优化目标函数,通常使用梯度下降法进行优化。
实践操作
下面我们将使用Scikit-learn库中的t-SNE类来实现数据降维。我们仍然使用Iris数据集作为示例。
from sklearn.manifold import TSNE
# 应用t-SNE
tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X_scaled)
# 可视化降维后的数据
plt.figure(figsize=(8, 6))
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap='viridis', edgecolor='k', s=80)
plt.xlabel('t-SNE Component 1')
plt.ylabel('t-SNE Component 2')
plt.title('t-SNE of Iris Dataset')
plt.show()
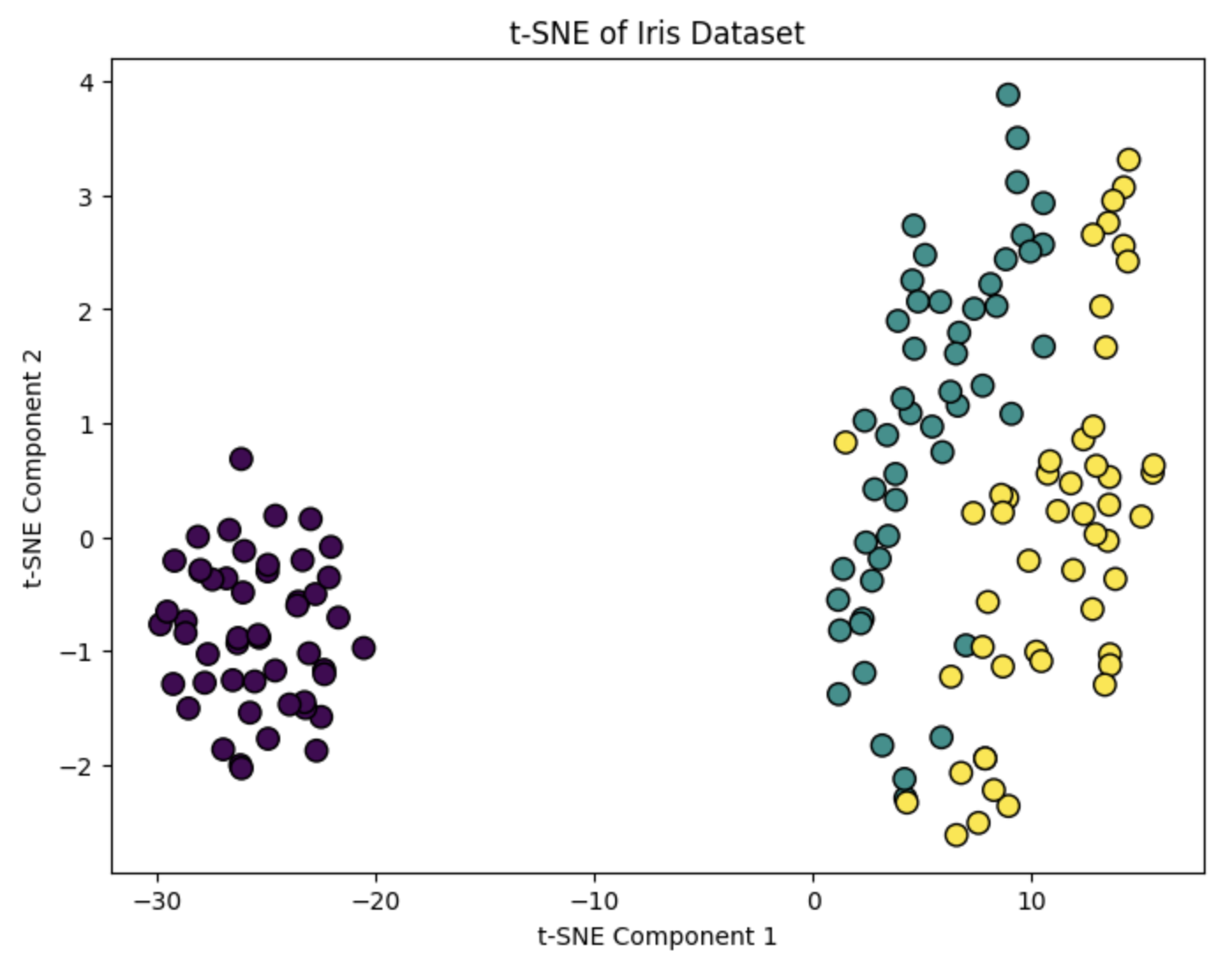
1.3 Scikit-learn中的降维方法
Scikit-learn库提供了多种降维方法,除了PCA和t-SNE之外,还包括LDA(线性判别分析)、ICA(独立成分分析)等。这些方法在不同的应用场景中各有优势,选择合适的降维方法需要根据具体的数据和任务来决定。
理论基础
- LDA(线性判别分析):LDA是一种监督学习的降维方法,通过最大化类间距离和最小化类内距离来实现数据的降维。LDA特别适用于分类任务。
- ICA(独立成分分析):ICA是一种盲源分离技术,通过寻找数据的独立成分来实现数据的降维。ICA在信号处理和图像处理等领域有广泛的应用。
实践操作
下面我们将使用Scikit-learn库中的LDA类来实现数据降维。我们仍然使用Iris数据集作为示例。
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 应用LDA
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit_transform(X, y)
# 可视化降维后的数据
plt.figure(figsize=(8, 6))
plt.scatter(X_lda[:, 0], X_lda[:, 1], c=y, cmap='viridis', edgecolor='k', s=80)
plt.xlabel('LDA Component 1')
plt.ylabel('LDA Component 2')
plt.title('LDA of Iris Dataset')
plt.show()
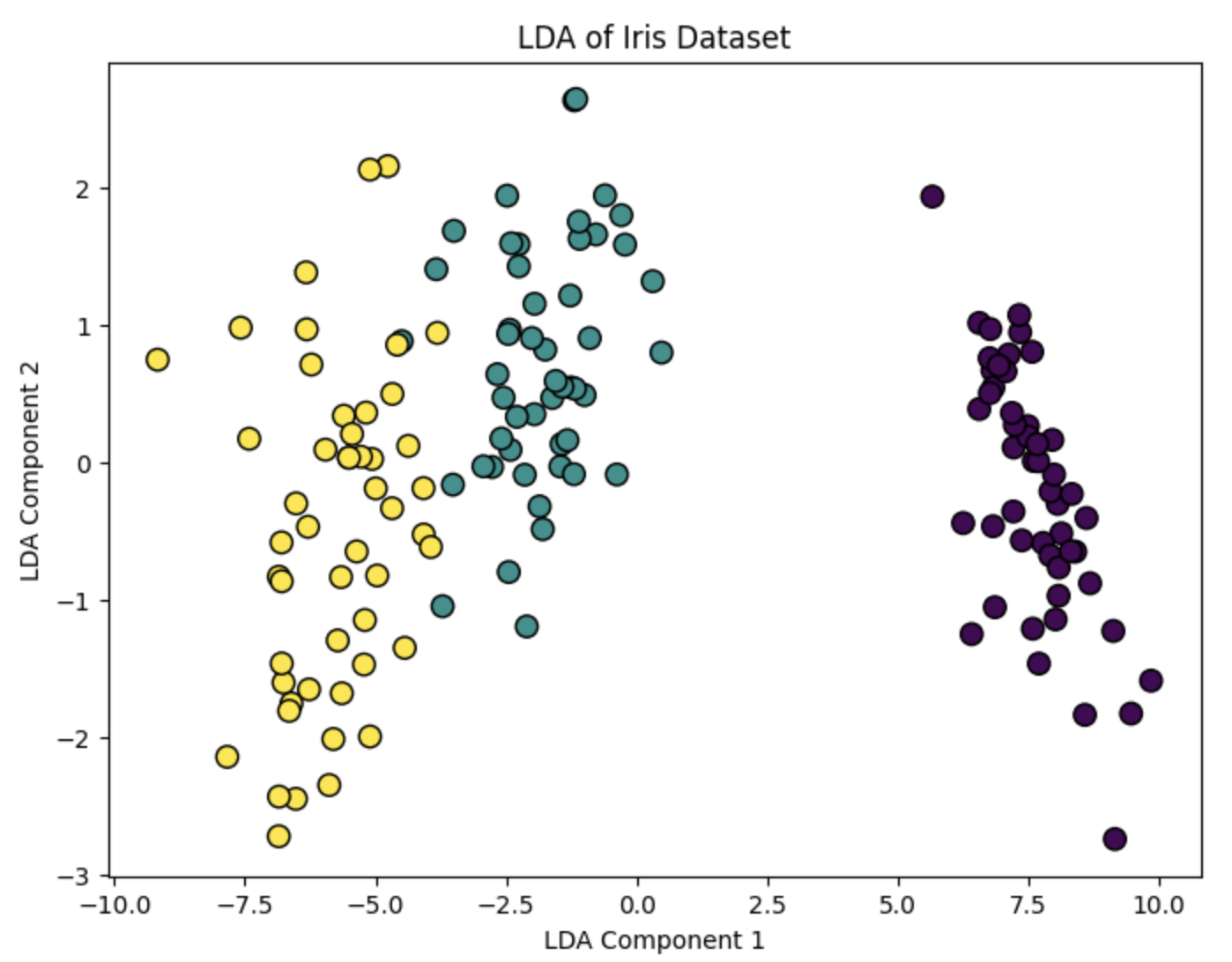
通过本课程的学习,学员将掌握PCA、t-SNE和LDA等降维方法的基本原理和实践操作,为后续的数据分析和机器学习任务打下坚实的基础。




















 693
693

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








