问题 如何采用离散补偿器提高离散化模型的精度和稳定性
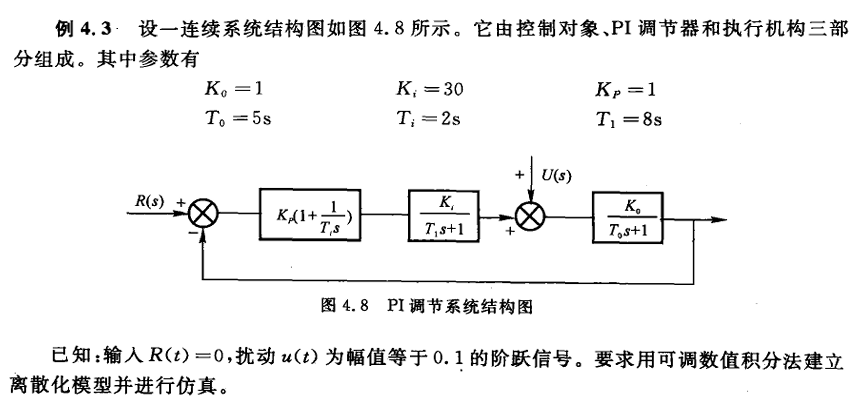
方案1
1) 参数与采样周期
已知参数(图中):

2) 被控对象、执行机构的 ZOH 精确离散化(第一阶系统)

这些表达式在直流与低频处与连续系统保持良好一致性,比简单差分法精度高。
3) PI 控制器用 Tustin(双线性)离散化(保留积分精度)

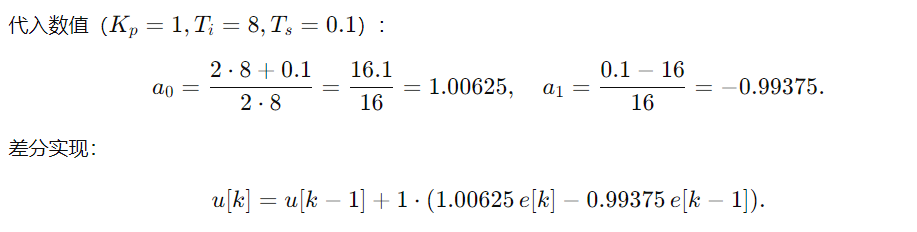
说明:
-
使用 Tustin(梯形法)能更好保持积分在低频处的累计(比前向欧拉或后向欧拉在相位与幅值上更准确)。
-
若对某一特定频率(如环交叉频率)需要精确匹配,可以在 Tustin 中对该频率做 预畸变(pre-warp)。
4) 细节

5) 最终仿真实现(步骤概要)

方案2

1 — 基本思想

2 — 图中方框的具体数学形式

3 — 并行计算与 z⁻¹ 延迟(为什么要在反馈里加一个 delay)
书上强调的一点:当环路中有若干个离散块“串联”时,如果在一次采样周期里把它们依次顺序更新,得到的结果与实际可在微控制器/数值仿真中“同时计算所有离散块、并把前一采样周期的输出作为输入” 的情况不同。工程实现常常是“在时刻 k,同时用上一次(时刻 k-1)的信号作为每个子环节的输入来计算这些子环节的 k 时刻新值”,因此后一个环节在实际运算中看到的是前一个环节在 k−1 时刻的输出,而不是刚刚计算出来的 k 时刻输出——这就产生了并行更新的模型差异。

4 — 具体实现伪代码(一步步写出如何在仿真/程序中计算)
假设某一子环节状态方程为
![]()
离散化步骤(在每个采样 k = 1,2,... 执行):
伪代码:
初始化: x_i[0] = x_i_init
保存: xdot_i_prev = a_i * x_i[0] + b_i * u_i_prev // u_i_prev 为 k=0 时刻的已知输入
for k = 1..N:
// 1) 计算当前导数近似(如果并行模型要求,u_i_use = u_i[k-1],否则可能用 u_i[k])
xdot_i_curr = a_i * x_i[k-1] + b_i * u_i_use
// 2) 状态更新(文献公式)
delta = lambda_i * Ts * ( gamma_i * xdot_i_curr + (1 - gamma_i) * xdot_i_prev )
x_i[k] = x_i[k-1] + delta
// 3) 准备下一步
xdot_i_prev = xdot_i_curr
end
注意:
-
u_i_use的取值要与图 4.10/4.11 中的延迟策略一致(并行实现通常是使用u_i[k-1])。 -
输出量通常是从状态或通过比例变换得到(例如在图中有
K0/T0等放大器块在状态之后)。 -
对于 PI 的积分环节,
a_i、b_i的具体值对应积分方程(例如对于积分器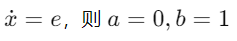 )。
)。
5 — λ、γ 的物理/数值意义与表 4.1(为何需要优化)

6 — 给出表中某组数值(举例,便于你直接代入)
(直接阅读表 4.1 的数值并列出,便于复制使用;表中的数字是书中通过数值优化得到的近似最优值。)
举例(从图中读出近似值):

7 — 与常见离散化方法的对比(表 4.2 的含义)
-
表 4.2 比较了三种方法在“平均相对误差 / 仿真精度”上的表现:

-
因此结论是:如果希望在较大采样周期下仍保持良好仿真精度,采用带参数调整的数值积分器(即书中方法)优于常规的 ZOH/零阶保持。
8 — 如何在你自己的仿真/控制器里使用这方法(步骤总结)






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








