间断特性的仿真 详细推导

饱和非线性间断特性平均函数的求法

第一步：理解饱和函数 (图 5.1 与 公式 5.10)

首先看右边的图 5.1。这是一个经典的饱和非线性特性 (Saturation Nonlinearity)。

通常我们用分段函数写它，很麻烦。但在数学推导中，为了方便积分，我们用了一个巧妙的绝对值公式来表达它，也就是书上的 (5.10) 式：

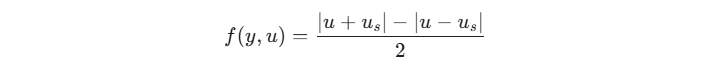
为什么这个式子等于图上的折线？我们来验证一下：

结论： 公式 (5.10) 就是图 5.1 的数学替身，目的是为了把分段函数变成一个统一的式子，方便后面做积分。

---

第二步：核心微积分知识点 (积分技巧)

这个推导中最难理解的一步，就是从积分符号变到方括号里的那一步。这里用到了一个大一微积分里不常强调，但工程数学里很好用的公式：

求绝对值函数的原函数：

---

第三步：详细推导过程解析

现在我们顺着书上的步骤把这一长串式子走一遍：

1. 定义平均函数 (Average Function)

2. 代入函数

5. 整理得到最终式 (5.11)

书上的 (5.11) 式就是把上面这一堆展开重新排列了一下。它把带 $\Delta u_n$ 的项和不带的项分别列出来了。

详细推导过程

准备工作：数学工具

在推导开始前，你需要且仅需要知道这一个积分公式：

---

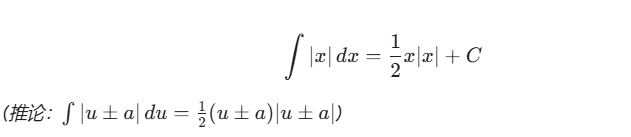
推导全过程

1. 明确已知条件

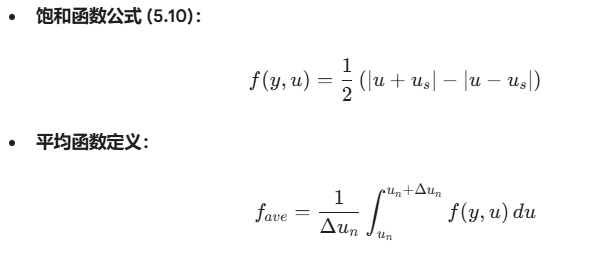
2. 代入函数并提取常数

3. 执行不定积分（寻找原函数）

4. 代入上下限 (牛顿-莱布尼茨公式)

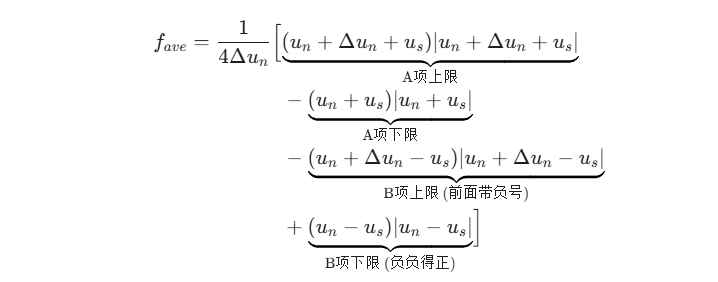
5. 去括号与重组 (得到最终结果)

将上面两部分合在一起，并把 B 项的负号分配进去（负负得正）：