不再死记！红黑树默认红色的原理 + LL/RR/LR/RL 全图解

🎬 个人主页：Vect个人主页

🎬 GitHub：Vect的代码仓库
🔥 个人专栏: 《数据结构与算法》《C++学习之旅》《计算机基础》

⛺️Per aspera ad astra.

---

---

1. 概念与性质

1.1. 概念

红黑树也是二叉搜索树，在每个节点上增加一个储存位表示节点的颜色，由RED和BLACK这两种颜色控制

通过任意一条从根到叶子的路径上各个节点着色方式的限制，红黑树确保了没有一条路径会比其他路径长出两倍，因而是接近平衡的。

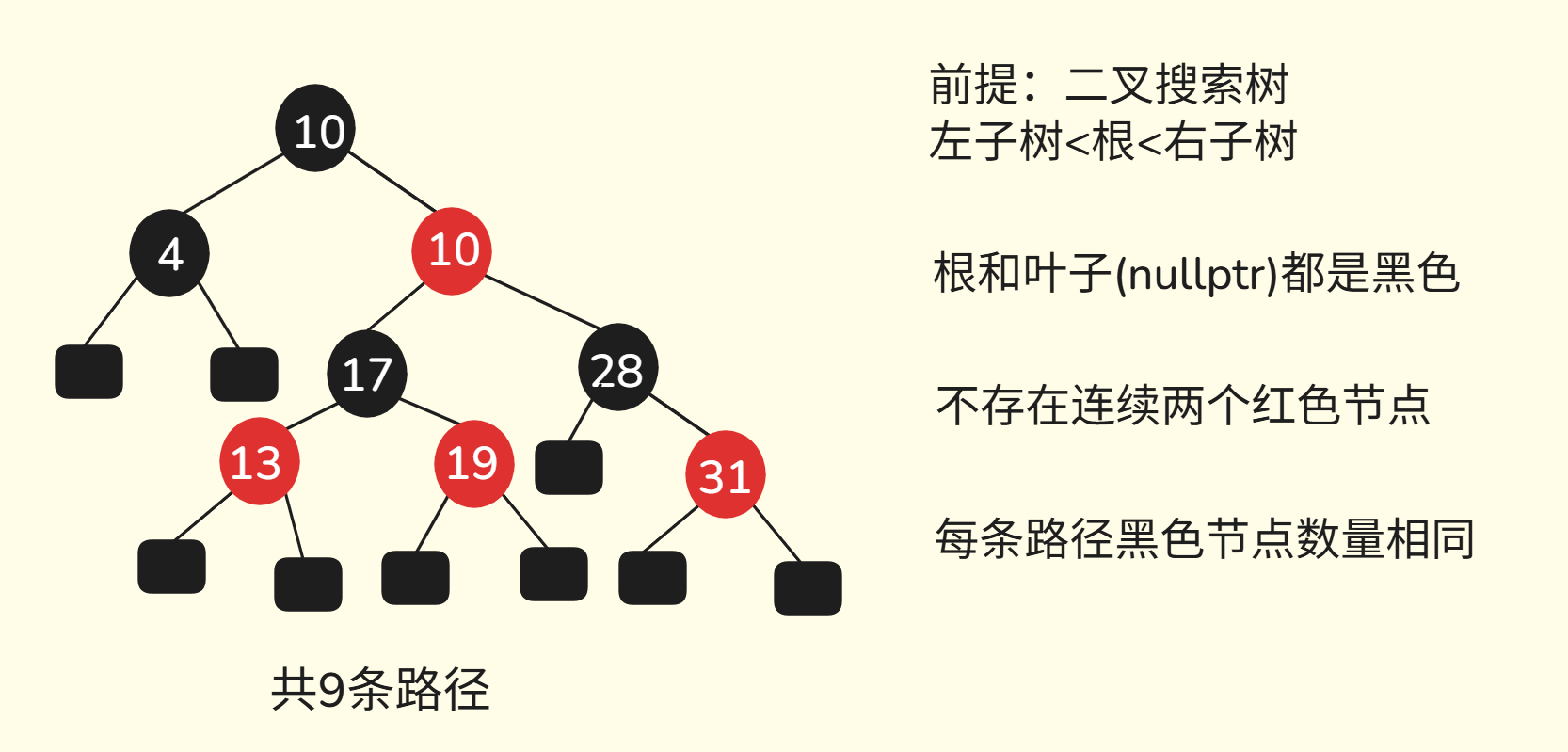
1.2. 性质

红黑树满足以下性质，缺一不可：

• 根节点是黑色（规定）
• 一条路径中，不能出现两个连续的红色节点
• 每条路径中，黑色的节点数目相同
• 叶节点（这里表示空节点），表示为NIL，全是黑色的

注意：这里的路径计算需要包含空节点

如下图所示：

1.3. 和其他树对比

无论是BST，AVL还是红黑树，每当插入删除节点后，如果树的性质被破坏，都要对树进行调整，来达到维护其性质的目的：

• BST：严格维护左<根<右的性质
• AVL树：在BST的基础上，严格维护左右子树高度差绝对值不大于1的性质
• 红黑树： 在BST的基础上，维护根和叶子黑色、不存在连续两个红色节点、每条路径黑色节点数目相同的性质

其实，只要搞清楚了这些树的性质，操作逻辑就很好理解了

而红黑树的引入，是为了解决AVL树插入和删除时，会经常调整树的结构，影响插入删除效率的问题

红黑树的插入删除效率比AVL树快

而红黑树的性质使得
$红黑树的最短路径\times 2>=红黑树的最长路径$

红黑树查找效率略低于AVL树，但二者仍是同一量级，可以忽略，所以红黑树的应用更加广泛

2. 红黑树节点的定义

	// 节点颜色
	enum Color { RED, BLACK };

	// 红黑树节点
	template<class K, class V>
	struct RBTreeNode {
		pair<K, V> _kv;
		RBTreeNode<K, V>* _left;
		RBTreeNode<K, V>* _right;
		RBTreeNode<K, V>* _parent;
		Color _col;

		// 构造
		RBTreeNode(const pair<K,V>& kv)
			:_kv(kv)
			,_left(nullptr)
			,_right(nullptr)
			,_parent(nullptr)
			,_col(RED)
		{ }
	};

	// 红黑树类
	template <class K,class V>
	class RBTree {
	public:
		typedef RBTreeNode<K, V> Node;
	private:
		Node* _root;
	};

这里构造函数，将颜色设置成红色，是为了便于插入时是红色节点，为什么插入时要用红色节点呢？

插入节点颜色选择无非是破坏性质2或性质3，我们考虑破坏哪条性质带来的代价会更小：

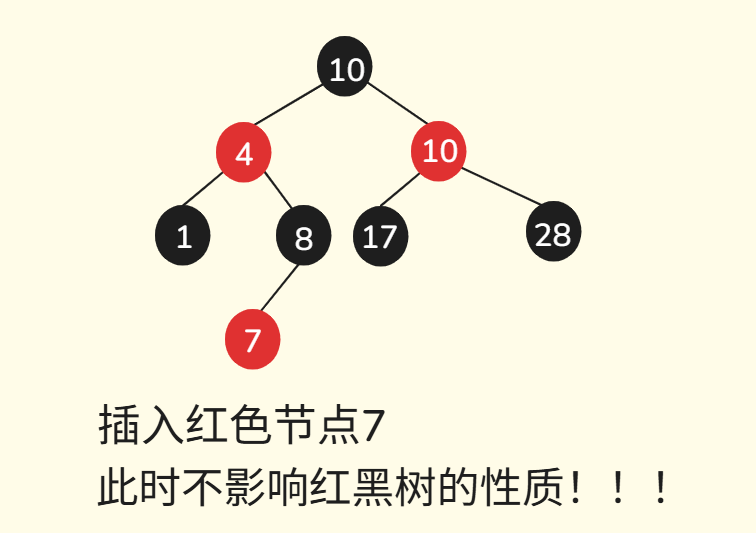
注意看，插入红色节点可能不需要调整，但是插入黑色节点，一定需要调整，为了方便后续操作，因此选择插入红色节点，那么构造函数构造红色节点也是方便插入操作

3. 插入节点

3.1. 按照二叉搜索树的方式寻找插入位置

// 1. 按照二叉搜索树方式 查找插入节点的位置
Node* cur = _root;
Node* parent = nullptr;

while (cur) {
	if (kv.first < cur->_kv.first) {
		parent = cur;
		cur = cur->_left;
	}
	else if (kv.first > cur->_kv.first) {
		parent = cur;
		cur = cur->_right;
	}
	else return false;						// 相同值 不插入 
}

// 2> 执行插入操作
// cur的位置就是待插入位置
cur = new Node(kv);
cur->_col = RED;
// parent为空 cur是根
if (parent == nullptr) {              // 空树：新节点为根
	_root = cur;
	cur->_parent = nullptr;
	return true;
}
// parent不为空 非空树
if (parent->_left == cur) parent->_left = cur
else parent->_right = cur;
cur->_parent = parent;

3.2. 检测新节点插入后 性质是否被破坏

因为新节点默认颜色是红色，

• 如果其父节点的颜色是黑色，就没有违反红黑树任何性质，无需调整
• 如果其父节点的颜色为红色时，违反了不能右连续两个红色节点的性质，此时需要分类讨论

3.2.1. 插入节点的叔叔节点(uncle)是红色

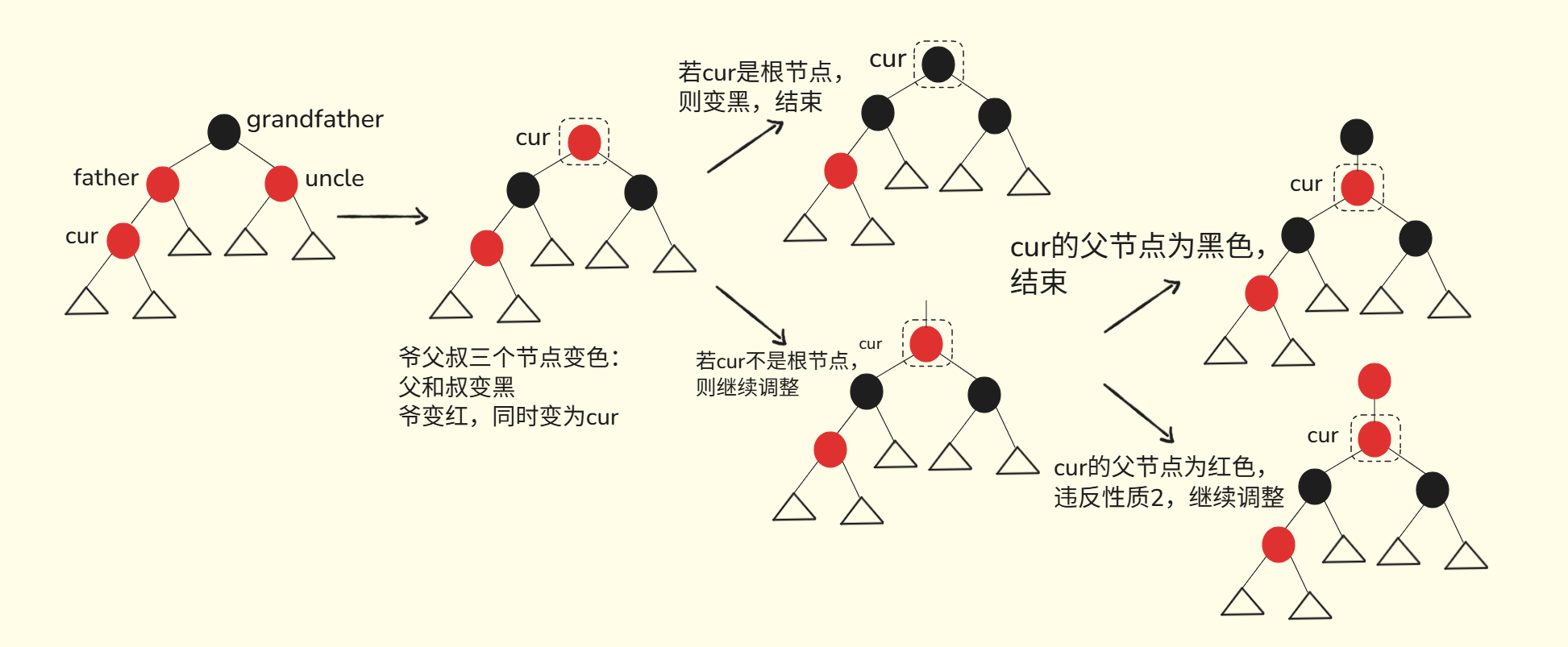
具体过程请看图

3.2.2. 插入节点的叔叔节点(uncle)是黑色

LL情况

RR情况

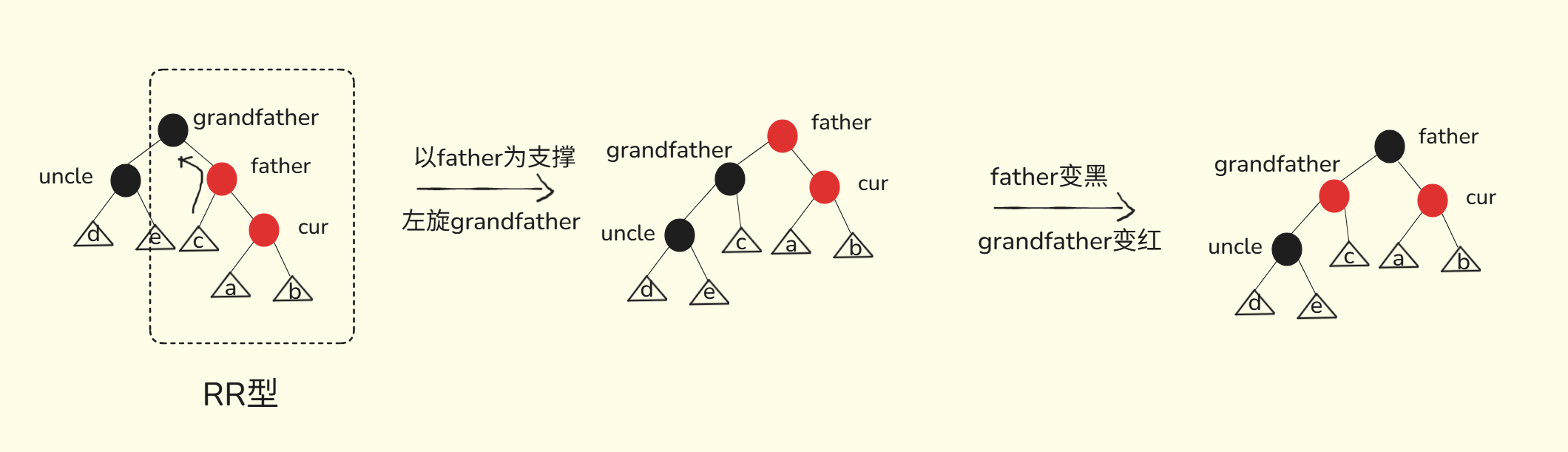
RL情况

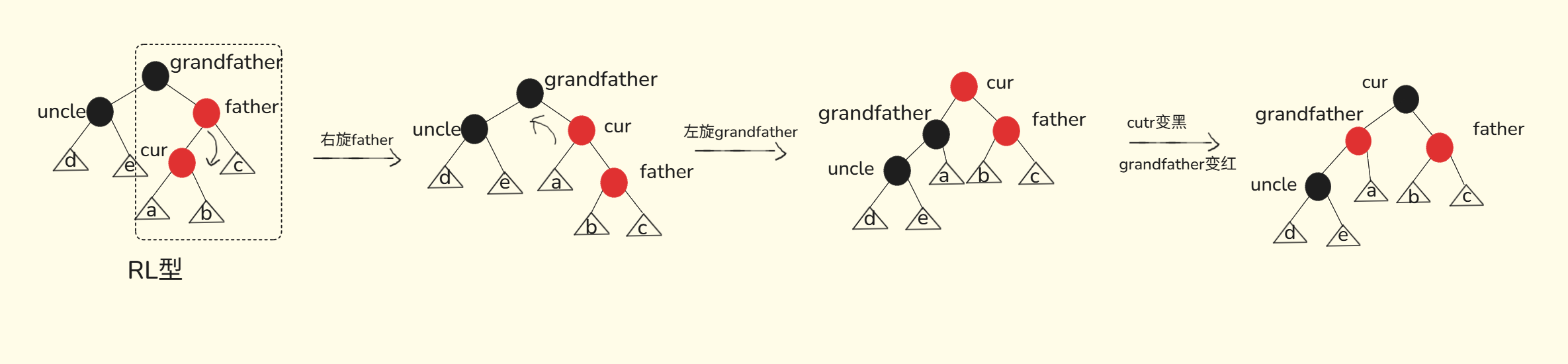
LR情况

代码实现

// 2. 检测新节点插入后 红黑树的性质是否造到破坏
// 父节点是黑色 插入的是红色 无影响 不用修改

// 父节点红色 插入的是红色 需要调整
while (parent && parent->_col == RED) {
    // 父为红 爷必为黑
    Node* grandfather = parent->_parent;
    if (grandfather && grandfather->left == parent) {
        Node* uncle = grandfather->_right;
        //  叔叔红色 只变色 不旋转
        //  父叔变黑 爷变红
        if (uncle && uncle->_col == RED) {
            grandfather->_col = RED;
            uncle->_col = parent->_col = BLACK;

            // 继续向上处理
            cur = grandfather;
            parent = cur->_parent;
        }
        else { // 叔叔黑色或不存在(不存在也是黑色)
            // LL
            if (parent->_left == cur) {
                /*		g黑
								   /   \
								  p红   u黑			LL 右旋
								 /
								c红
				*/
                rotateRight(grandfather);
                parent->_col = BLACK;
                grandfather->_col = RED;
            }
            else { // parent->_eight == cur
                // 先对parent左旋 转成LL 再按照LL处理
                rotateLeft(parent);
                // cur上来称为中间节点
                // 右旋爷 新根黑 原爷红
                rotateRight(grandfather);
                cur->_col = BLACK;
                grandfather->_col = RED;
            }
            break; // LL LR一次旋转即可退出循环
        }
    }
    else { // !(grandfather && grandfather->left == parent)
        // parent是grandfather的右孩子
        Node* uncle = grandfather ? grandfather->_right : nullptr;

        if (uncle && uncle->_col == RED) {
            grandfather->_col = RED;
            uncle->_col = parent->_col = BLACK;

            cur = grandfather;
            parent = cur->_parent;
        }
        else {
            // 叔叔为黑或不存在（也为黑）
            if (parent->_right == cur) {
                /*
							   g黑
							   /   \
							  u黑   p红			RR 左旋
									   \
										c红
				*/
                rotateLeft(grandfather);
                parent->_col = BLACK;
                grandfather->_col = RED;
            }
            else {
                rotateRight(parent);
                rotateLeft(grandfather);[添加链接描述](https://blog.youkuaiyun.com/Vect__/article/details/154140919?spm=1011.2124.3001.6209)
                cur->_col = BLACK;
                grandfather->_col = RED;
            }
            break;
        }
    }
}
_root->_col = BLACK; // 最后强制根为黑 防止上面操作将根染红
return true;

对于旋转操作：请详见这篇文章：别再让搜索树变竹竿！AVL 旋转四连招详解！

完整代码和图片请移步我的GitHub：Vect的代码仓