排序算法精讲-优快云博客

本文链接：https://blog.youkuaiyun.com/VargrantS/article/details/98228475

一、基本概念

稳定性：当待排序列中有两个或两个以上相同的关键字时，排序前后这些关键字的相对位置若没有发生改变，则说排序算法是稳定的；
排序算法分类：插入排序、交换排序、选择排序、归并排序、基数排序、外部排序；

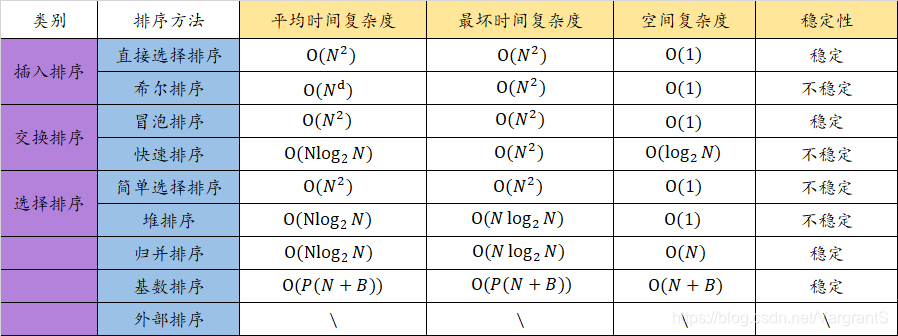
在这里插入图片描述

二、插入类

1. 直接插入排序

void InsertSort(ElementType A[], int N)
{
	int P, i;
	ElementType Tmp;

	for (P = 1; P < N; P++) {
		Tmp = A[P];
		for (i = P; i > 0 && A[i - 1] > Tmp; i--)
			A[i] = A[i - 1];
		A[i] = Tmp;
	}
}

PS：对于一个已经基本有序的序列，也可以采用折半插入法（利用二分查找的方式来寻找插入位置）；

2. 希尔排序（缩小增量排序）

/* 原始希尔排序 */
void ShellSort(ElementType A[], int N)
{
	for (D = N / 2; D > 0; D /= 2) {
		for (P = D; P < N; P++) {
			Tmp = A[P];
			for (i = P; i >= D && A[i - D] > Tmp; i -= D)
				A[i] = A[i - D];
			A[i] = Tmp;
		}
	}
}

/* Sedgewick 增量序列 */
void ShellSort_Sedgewick(ElementType A[], int N)
{
	int Si, D, P, i;
	ElementType Tmp;
	/* 这里只列出一小部分增量 */
	int Sedgewick[] = { 929, 505, 209, 109, 41, 19, 5, 1, 0 };
	// 9*(4^i)-9*(2^i)+1 或 (4^i)-3*(2^i)+1

	for (Si = 0; Sedgewick[Si] >= N; Si++)
		; /* 初始的增量Sedgewick[Si]不能超过待排序列长度 */

	for (D = Sedgewick[Si]; D > 0; D = Sedgewick[++Si])
		for (P = D; P < N; P++) { /* 插入排序*/
			Tmp = A[P];
			for (i = P; i >= D && A[i - D] > Tmp; i -= D)
				A[i] = A[i - D];
			A[i] = Tmp;
		}
}

注意事项：

增量序列的最后一个值一定取 1 ；
增量序列中的值应尽量没有除 1 以外的公因子；
对于不同的增量序列，其时间复杂度有所区别；
3.1 原始希尔排序的最坏时间复杂度为 $O(N^2)$
3.2 Papernov & Stasevich序列： $O(N^{1.5})$ 【 $2^{k}+1、...、65、33、17、9、5、3、1$ 】
3.3 Sedgewick 序列： $T_{avg} = O(N^{7/6}), T_{worst}=O(N^{4/3})$

三、交换类

1. 冒泡排序

void BubbleSort(ElementType A[], int N)
{
	int flag = 0;
	for (int i = N - 1; i >= 0; i--) {
		flag = 0;
		for (int j = 0; j < i; j++) {
			if (A[j] > A[j + 1]) {
				swap(A[j], A[j + 1]);
				flag = 1;
			}
		}
		if (flag == 0)	//全程无交换
			break;
	}
}

注意事项：

算法结束条件：在一趟排序过程中没有发生关键字交换；

2. 快速排序

/* 快速排序 */

ElementType Median(ElementType A[], int Left, int Right)
{	//pivot 取中位数
	int Center = (Left + Right) / 2;
	if (A[Left] > A[Center])
		swap(A[Left], A[Center]);
	if (A[Left] > A[Right])
		swap(A[Left], A[Right]);
	if (A[Center] > A[Right])
		swap(A[Center], A[Right]);
	/* 此时A[Left] <= A[Center] <= A[Right] */
	swap(A[Center], A[Right - 1]); /* 将基准Pivot藏到右边*/
	/* 只需要考虑A[Left+1] … A[Right-2] */
	return  A[Right - 1];  /* 返回基准Pivot */
}

void Qsort(ElementType A[], int Left, int Right)
{ /* 核心递归函数 */
	int Pivot, Cutoff, Low, High;
	// 数据量小时可直接使用插入排序
	Cutoff = 30;

	if (Cutoff <= Right - Left) { /* 如果序列元素充分多，进入快排 */
		Pivot = Median(A, Left, Right); /* 选基准 */
		Low = Left; High = Right - 1;
		while (1) { /*将序列中比基准小的移到基准左边，大的移到右边*/
			while (A[++Low] < Pivot);
			while (A[--High] > Pivot);
			if (Low < High) swap(A[Low], A[High]);
			else break;
		}
		swap(A[Low], A[Right - 1]);   /* 将基准换到正确的位置 */
		Qsort(A, Left, Low - 1);    /* 递归解决左边 */
		Qsort(A, Low + 1, Right);   /* 递归解决右边 */
	}
	else InsertSort(A + Left, Right - Left + 1); /* 元素太少，用简单排序 */
}

void QuickSort(ElementType A[], int N)
{ /* 统一接口 */
	Qsort(A, 0, N - 1);
}

三、选择类排序

1. 选择排序

算法介绍：遍历序列找出最小关键字后与第一个关键字交换，之后再对剩余序列进行重复操作即可；

2. 堆排序

void PercDown(ElementType A[], int p, int N)
{
  /* 将N个元素的数组中以A[p]为根的子堆调整为最大堆 */
	int Parent, Child;
	ElementType X;

	X = A[p]; /* 取出根结点存放的值 */
	for (Parent = p; (Parent * 2 + 1) < N; Parent = Child) {
		Child = Parent * 2 + 1;
		if ((Child != N - 1) && (A[Child] < A[Child + 1]))
			Child++;  /* Child指向左右子结点的较大者 */
		if (X >= A[Child]) break; /* 找到了合适位置 */
		else  /* 下滤X */
			A[Parent] = A[Child];
	}
	A[Parent] = X;
}

void HeapSort(ElementType A[], int N)
{ 
	for (int i = N / 2 - 1; i >= 0; i--)/* 建立最大堆 */
		PercDown(A, i, N);

	for (int i = N - 1; i > 0; i--) {
		/* 删除最大堆顶 */
		swap(A[0], A[i]);
		PercDown(A, 0, i);
	}
}

四、其他类型排序

1. 归并排序

 /* 归并排序 - 递归实现 */
void MergeSort1(ElementType A[], int N)
{
	// 此处声明临时数组是为了整体节省时间，避免在递归式中反复声明.
	ElementType *TmpA;
	TmpA = (ElementType *)malloc(N * sizeof(ElementType));

	if (TmpA != NULL) {
		Msort(A, TmpA, 0, N - 1);
		free(TmpA);
	}
	else printf("空间不足");
}

void Msort(ElementType A[], ElementType TmpA[], int L, int RightEnd)
{ /* 核心递归排序函数 */
	int Center;
	if (L < RightEnd) {
		Center = (L + RightEnd) / 2;
		Msort(A, TmpA, L, Center);              /* 递归解决左边 */
		Msort(A, TmpA, Center + 1, RightEnd);     /* 递归解决右边 */
		Merge(A, TmpA, L, Center + 1, RightEnd);  /* 合并两段有序序列 */
	}
}

/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/
void Merge(ElementType A[], ElementType TmpA[], int L, int R, int RightEnd)
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
	int LeftEnd, NumElements, Tmp;
	LeftEnd = R - 1; /* 左边终点位置 */
	Tmp = L;         /* 有序序列的起始位置 */
	NumElements = RightEnd - L + 1;

	while (L <= LeftEnd && R <= RightEnd) {
		if (A[L] <= A[R])
			TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
		else
			TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
	}

	while (L <= LeftEnd)
		TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
	while (R <= RightEnd)
		TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */

	// 循环实现时不需要
	for (int i = 0; i < NumElements; i++, RightEnd--)
		A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */
}
/* ------------------------------------------------------------- */
/* 归并排序 - 循环实现 */
void MergeSort2(ElementType A[], int N)
{
	int length;
	ElementType *TmpA;
	length = 1; /* 初始化子序列长度*/
	TmpA = (ElementType *)malloc(N * sizeof(ElementType));
	if (TmpA != NULL) {
		while (length < N) {
			Merge_pass(A, TmpA, N, length);
			length *= 2;
			Merge_pass(TmpA, A, N, length);
			length *= 2;
		}
		free(TmpA);
	}
	else printf("空间不足");
}
/* length = 当前有序子列的长度*/
void Merge_pass(ElementType A[], ElementType TmpA[], int N, int length)
{ /* 两两归并相邻有序子列 */
	int i;
	for (i = 0; i <= N - 2 * length; i += 2 * length)
		Merge(A, TmpA, i, i + length, i + 2 * length - 1);

	if (i + length < N) /* 归并最后2个子列*/
		Merge(A, TmpA, i, i + length, N - 1);
	else /* 最后只剩1个子列*/
		for (int j = i; j < N; j++)
			TmpA[j] = A[j];
}

2. 桶排序与基数排序

主位优先（MSD）：即先按最高位排成若干子序列，再对每个子序列按次高位进行排序；
次位优先（LSD）：不需要分成子序列，每次排序全体关键字都要参与；
平均和最坏时间复杂度均为 $O (P (N + B))$ ，其中 $P$ 表示关键字位数， $B$ 表示关键字基的个数

    /* 基数排序 - 主位优先 */
    /* 假设元素最多有MaxDigit个关键字，基数全是同样的Radix */
    #define MaxDigit 4
    #define Radix 10
     
    /* 桶元素结点 */
    typedef struct Node *PtrToNode;
    struct Node{
        int key;
        PtrToNode next;
    };
     
    /* 桶头结点 */
    struct HeadNode {
        PtrToNode head, tail;
    };
    typedef struct HeadNode Bucket[Radix];
      
    int GetDigit ( int X, int D )
    { /* 默认次位D=1, 主位D<=MaxDigit */
        int d, i;
         
        for (i=1; i<=D; i++) {
            d = X%Radix;
            X /= Radix;
        }
        return d;
    }
     
    void MSD( ElementType A[], int L, int R, int D )
    { /* 核心递归函数: 对A[L]...A[R]的第D位数进行排序 */
         int Di, i, j;
         Bucket B;
         PtrToNode tmp, p, List = NULL; 
         if (D==0) return; /* 递归终止条件 */
          
         for (i=0; i<Radix; i++) /* 初始化每个桶为空链表 */
             B[i].head = B[i].tail = NULL;
         for (i=L; i<=R; i++) { /* 将原始序列逆序存入初始链表List */
             tmp = (PtrToNode)malloc(sizeof(struct Node));
             tmp->key = A[i];
             tmp->next = List;
             List = tmp;
         }
         /* 下面是分配的过程 */
         p = List;
         while (p) {
             Di = GetDigit(p->key, D); /* 获得当前元素的当前位数字 */
             /* 从List中摘除 */
             tmp = p; p = p->next;
             /* 插入B[Di]号桶 */
             if (B[Di].head == NULL) B[Di].tail = tmp;
             tmp->next = B[Di].head;
             B[Di].head = tmp;
         }
         /* 下面是收集的过程 */
         i = j = L; /* i, j记录当前要处理的A[]的左右端下标 */
         for (Di=0; Di<Radix; Di++) { /* 对于每个桶 */
             if (B[Di].head) { /* 将非空的桶整桶倒入A[], 递归排序 */
                 p = B[Di].head;
                 while (p) {
                     tmp = p;
                     p = p->next;
                     A[j++] = tmp->key;
                     free(tmp);
                 }
                 /* 递归对该桶数据排序, 位数减1 */
                 MSD(A, i, j-1, D-1);
                 i = j; /* 为下一个桶对应的A[]左端 */
             } 
         } 
    }
     
    void MSDRadixSort( ElementType A[], int N )
    { /* 统一接口 */
        MSD(A, 0, N-1, MaxDigit); 
    }
    
    /* 基数排序 - 次位优先 */
    /* 假设元素最多有MaxDigit个关键字，基数全是同样的Radix */
    #define MaxDigit 4
    #define Radix 10
     
    /* 桶元素结点 */
    typedef struct Node *PtrToNode;
    struct Node {
        int key;
        PtrToNode next;
    };
     
    /* 桶头结点 */
    struct HeadNode {
        PtrToNode head, tail;
    };
    typedef struct HeadNode Bucket[Radix];
      
    int GetDigit ( int X, int D )
    { /* 默认次位D=1, 主位D<=MaxDigit */
        int d, i;
         
        for (i=1; i<=D; i++) {
            d = X % Radix;
            X /= Radix;
        }
        return d;
    }
     
    void LSDRadixSort( ElementType A[], int N )
    { /* 基数排序 - 次位优先 */
         int D, Di, i;
         Bucket B;
         PtrToNode tmp, p, List = NULL; 
          
         for (i=0; i<Radix; i++) /* 初始化每个桶为空链表 */
             B[i].head = B[i].tail = NULL;
         for (i=0; i<N; i++) { /* 将原始序列逆序存入初始链表List */
             tmp = (PtrToNode)malloc(sizeof(struct Node));
             tmp->key = A[i];
             tmp->next = List;
             List = tmp;
         }
         /* 下面开始排序 */ 
         for (D=1; D<=MaxDigit; D++) { /* 对数据的每一位循环处理 */
             /* 下面是分配的过程 */
             p = List;
             while (p) {
                 Di = GetDigit(p->key, D); /* 获得当前元素的当前位数字 */
                 /* 从List中摘除 */
                 tmp = p; p = p->next;
                 /* 插入B[Di]号桶尾 */
                 tmp->next = NULL;
                 if (B[Di].head == NULL)
                     B[Di].head = B[Di].tail = tmp;
                 else {
                     B[Di].tail->next = tmp;
                     B[Di].tail = tmp;
                 }
             }
             /* 下面是收集的过程 */
             List = NULL; 
             for (Di=Radix-1; Di>=0; Di--) { /* 将每个桶的元素顺序收集入List */
                 if (B[Di].head) { /* 如果桶不为空 */
                     /* 整桶插入List表头 */
                     B[Di].tail->next = List;
                     List = B[Di].head;
                     B[Di].head = B[Di].tail = NULL; /* 清空桶 */
                 }
             }
         }
         /* 将List倒入A[]并释放空间 */
         for (i=0; i<N; i++) {
            tmp = List;
            List = List->next;
            A[i] = tmp->key;
            free(tmp);
         } 
    }