计算机图形学----光线追踪----路径追踪

基础知识预备

概率论

概率

期望= ∑（概率*值）

PDF (概率密度函数)
概率密度函数：p(x)在数学中，连续型随机变量的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。也就是结果为某个值得可能性描述。
性质：
p(x)概率密度函数积分为1.
x*p(x)积分为期望

Monte Carlo Integration（蒙特卡洛积分）

蒙特卡洛积分
在积分域内不断去采样，采样到y值，做很多次采样。对所有采样做平均。采样的次数越少，越不准，采样的次数越多，越准确。

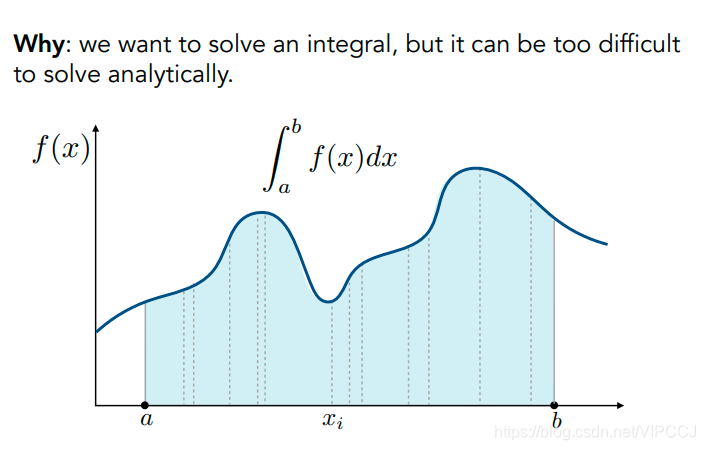
在x采样，在x积分。采样和积分在一个域。

Path Tracing(路径追踪)

路径追踪，光线在场景中的传播，最终模拟出和真实世界一样的画面。

第一步：假设我们需要渲染一个像素，且只考虑直接光照（光源）的影响，应该怎么做呢？

渲染方程如下，不考虑自发光

L(颜色) = ∑ 每个方向(只考虑光源)过来的radiance * BRDF * (夹角的cos)

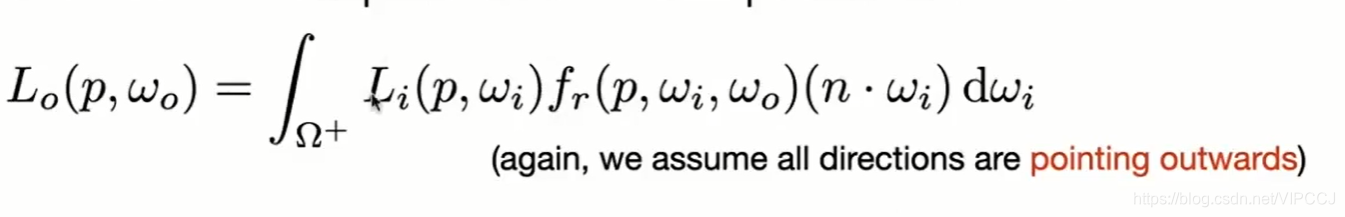
使用蒙特卡洛积分解决：

随机取一个方向，使用蒙特卡洛积分（对半球进行均匀采样）概率密度为1/2π

任何一个着色点，出射方向的Lo

着色算法（直接光照）：
前提条件：只考虑直接光照
对于某个着色点p，向某一个方向wi发出一条光线，和光源做连线。
如果可以连到光源，那么计算该点在该方向上，收到光源光照的颜色。

Introducting Global Illumination（全局光照）
如果p在wi发出的一条线，没有打到光源，而是打到某个物体上，这一条光路对p点的颜色有什么影响呢？

答案是有影响，我们把p-wi光路交点q假设成一个光源，还可以用蒙特卡洛积分描述这条光路对p点颜色的影响。

结论：

对于一个着色点p,我们总是从p点某个方向发出一条光线，打到光源或者物体后，计算光源或者物体对p点颜色影响，公式如下：

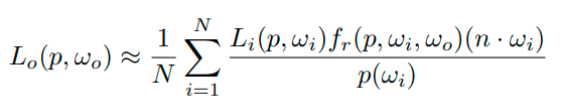
那么，该点的颜色就是在0~2π区域内发出所有光线的积分
存在问题：
1.算量爆炸光线弹射次数爆炸指数爆炸

2.光线什么时候弹射停止，无限弹射？

**问题一：算量爆炸光线弹射次数爆炸指数爆炸 **

假设一个着色点，随机选择一个方向，只打出一个光线。N=1 也就是光线的弹射次数为1.

弹射次数为1，但是对于每一个像素会依然会有很多路径对该像素点着色，对所有路径的着色求平均，就是路径追踪。

对于一个像素，可以选择很多条路径，对于每一个像素的颜色，结果是N条路径给这个像素着色结果的平均。

问题二：递归什么时候停止 俄罗斯轮盘赌

对结果除以p,俄罗斯轮盘赌的期望还是Lo，所以说，俄罗斯轮盘赌是五偏的

路径追踪算法：（加入俄罗斯轮盘赌）

路径追踪算法：不同spp结果比较

对光源积分
第一个场景：发出5根光线打到光源
第二个场景：500
第三个场景：50000
所以其实我们路径追踪中有很多path是没有作用的，因为这个path最终回不到光源。

对光源积分，就需要对光源采样
对光源采样，需要对光源积分，我们之前的路径追踪是在立体角上积分。对于面光源来讲,
pdf = 1 / A(面积),但是我们需要对光源积分，才能改写路径追踪的算法。
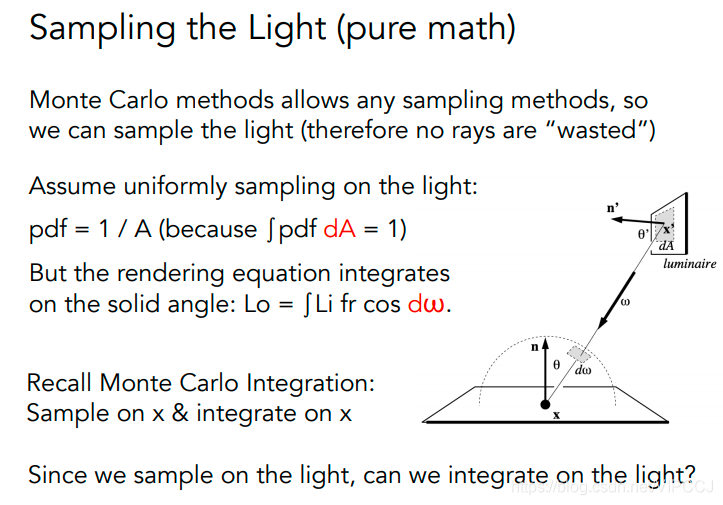如何做转换
考虑dw（立体角）和dA（光源的表面）的关系，dA投影到半球上的面积，就是dw。

重写渲染方程：
其实就是积分的变量替换，将dw替换为dA，积分域从2π替换为面光源的面积A

重写路径追踪：
一个着色点的颜色：
1.光源的直接贡献（写为对光源积分）
2.非光源的贡献( 常规算法)

直接光照+间接光照

对光源进行采样，考虑遮挡

路径追踪和真实照片

截图和公式来源闫令琪老师games101课程
感谢闫令琪老师为我们带来这么精彩的图形学课程
https://www.bilibili.com/video/BV1X7411F744?p=16