代码随想录算法训练营第 46 天 | 647. 回文子串、516. 最长回文子序列

最新推荐文章于 2025-12-22 09:47:08 发布

原创最新推荐文章于 2025-12-22 09:47:08 发布 · 165 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法

算法训练营专栏收录该内容

53 篇文章

订阅专栏

647. 回文子串

题目链接

dp[i][j]：[i, j]（左闭右闭）的字符串是不是回文子串。

递推公式：

if (s.charAt(i) == s.charAt(j))

j = i：dp[i][j] = true（只有一个字符）
j - i = 1：dp[i][j] = true（只有两个字符）
j - i >= 2：dp[i][j] = dp[i + 1][j - 1]（取决于中间字符串）

前两种情况可以合并。

if (s.charAt(i) != s.charAt(j))

dp[i][j] = false

初始化：全部初始化为 false。

遍历顺序：从下到上，从左到右（假设 j >= i）
（因为根据递推公式，是从左下角往右上角推导的。）

class Solution {
    public int countSubstrings(String s) {
        int n = s.length();
        boolean[][] dp = new boolean[n][n]; // dp[i][j]：[i, j]（左闭右闭）的字符串是不是回文子串。
        // 初始化：全部初始化为 false。

        int result = 0;
        for (int i = n - 1; i >= 0; i--) { // 遍历顺序：从下到上，从左到右（假设 j >= i）
            for (int j = i; j < n; j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    if (Math.abs(j - i) <= 1) {
                        dp[i][j] = true;
                        result++;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                        if (dp[i][j]) {
                            result++;
                        }
                    }
                } else {
                    dp[i][j] = false;
                }
            }
        }

        return result;
    }
}

516. 最长回文子序列

题目链接

子序列：可以不连续。
上题的子串：要求必须连续。

dp[i][j]：[i, j] 字符串的最长回文子序列长度。(不一定连续)

递推公式：

if (s.charAt(i) == s.charAt(j))

dp[i][j] = dp[i + 1][j - 1] + 2

if (s.charAt(i) != s.charAt(j))

dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1])

初始化：
因为只需对矩阵右上三角便利，所以从左上到右下的对角线需初始化。初始化为 1。

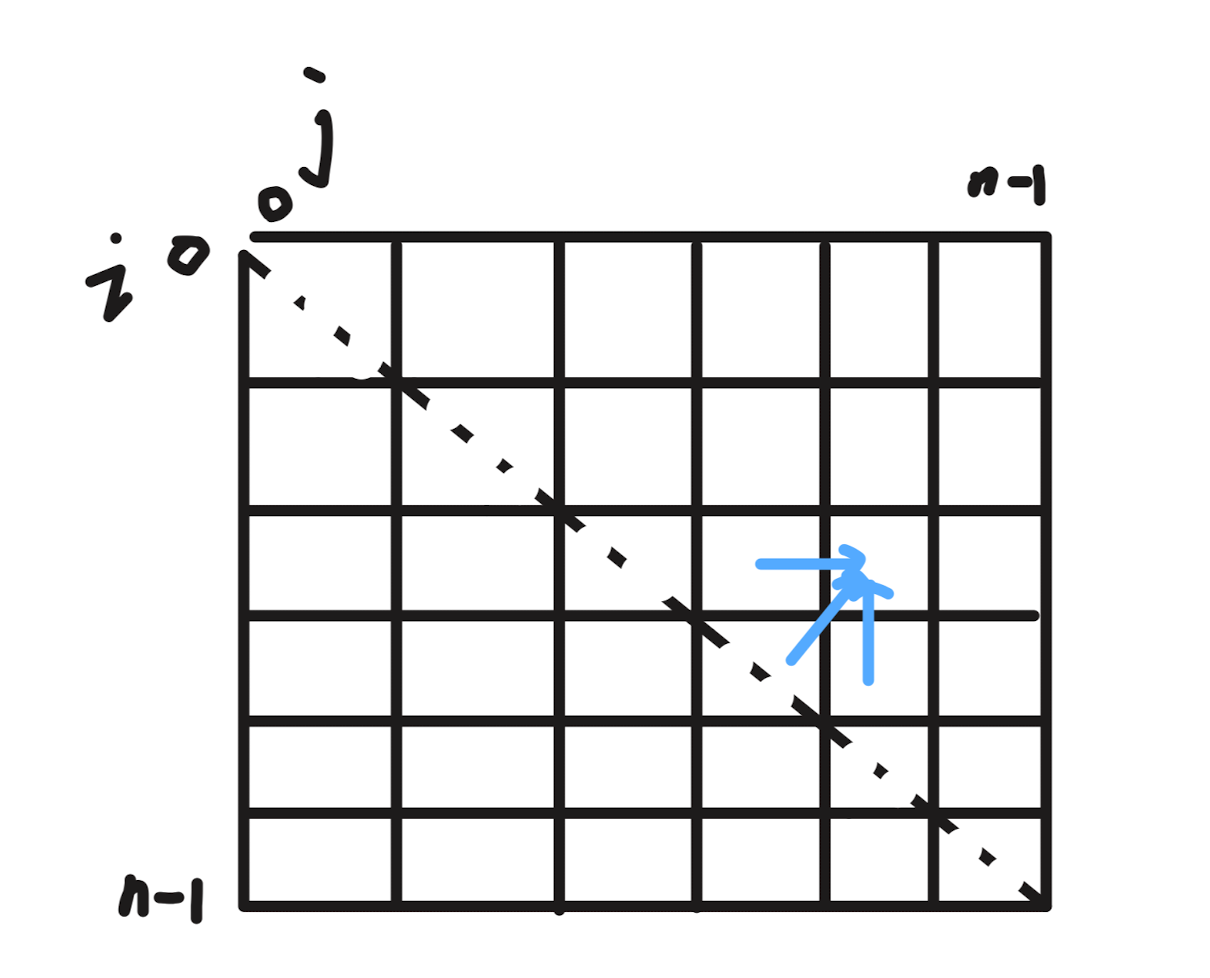
在这里插入图片描述

遍历顺序：
从下到上，从左到右。

class Solution {
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        int[][] dp = new int[n][n]; // dp[i][j]：[i, j] 字符串的最长回文子序列长度。(不一定连续)

        for (int i = 0; i < n; i++) { // 初始化：i = j 时，dp[i][i] 初始化为 1。
            dp[i][i] = 1;
        }

        for (int i = n - 1; i >= 0; i--) {
            for (int j = i + 1; j < n; j++) { // 因为是右上三角，所以 i = j 的对角线要初始化。
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2; // 如果 j - i = 1，这个公式计算出来的结果是 2，也成立。
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[0][n - 1];
    }
}