代码随想录算法训练营第 2 天 | 209. 长度最小的子数组、59. 螺旋矩阵 II

209. 长度最小的子数组

题目链接

我用的双指针，官解用的滑动窗口，其实本质一样

我的解法：快慢指针（一层循环）

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        // 1 <= nums.length <= 10^5
        int n = nums.length;
        int ans = Integer.MAX_VALUE;
        int slow = 0;
        int fast = 0;
        int sum = nums[slow];
        for (; fast <= n - 1; ) {
            if (sum < target) {
                fast++;
                if (fast <= n - 1) {
                    sum += nums[fast];
                }
            } else {
                sum -= nums[slow];
                ans = Math.min(ans, fast - slow + 1);
                slow++;
            }
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }
}

——不足之处：sum += nums[fast] 得额外判断一次数组有没有溢出

不如官解：

class Solution {
    public int minSubArrayLen(int s, int[] nums) {
        int n = nums.length;
        if (n == 0) {
            return 0;
        }
        int ans = Integer.MAX_VALUE;
        int start = 0, end = 0;
        int sum = 0;
        while (end < n) {
            sum += nums[end];
            while (sum >= s) {
                ans = Math.min(ans, end - start + 1);
                sum -= nums[start];
                start++;
            }
            end++;
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }
}

——使用两层循环，思路更清晰

终止位置 end，起始位置 start
先移动终止位置
sum 统计滑动窗口的和，如果大于等于 target，就开始移动起始位置，直到 sum 小于 target
这个过程中收集最小值 ans

59. 螺旋矩阵 II

题目链接

重难点：

1. 区间定义成左闭右开
2. offset 的设计很巧妙

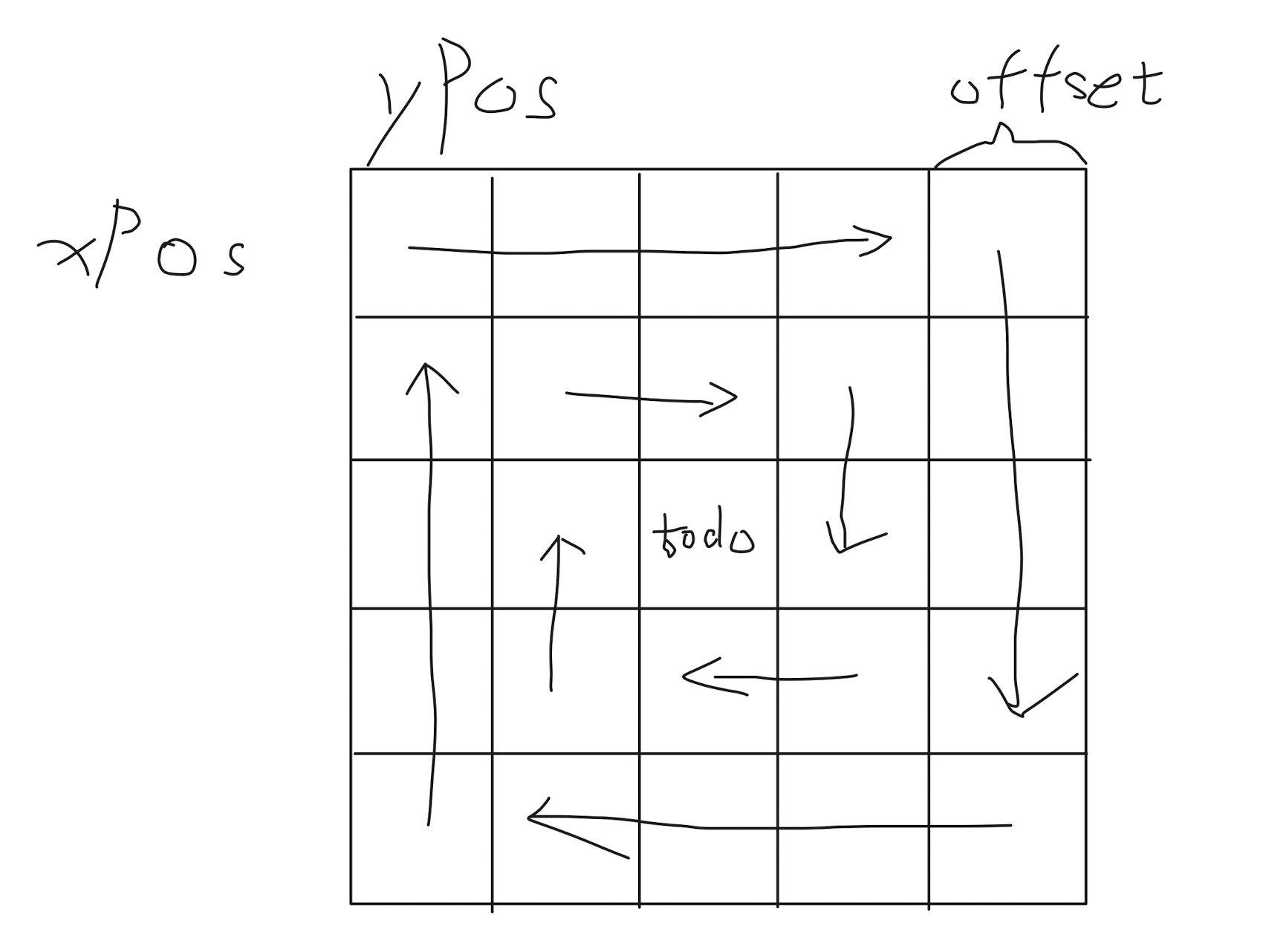
易错点：

• xPos 和 yPo 在走完一圈后也要加 1
• n 为奇数要补上最中心的数字

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] ans = new int[n][n];
        int count = 1; // 生成的数
        int offset = 1; // 每一轮与侧边的距离
        int turn = n / 2; // 圈数
        int xPos = 0, yPos = 0;
        for (int i = 0; i < turn; i++) { // 转 n/2 圈
            for (; yPos < n - offset; yPos++) {
                ans[xPos][yPos] = count++;
            }
            for (; xPos < n - offset; xPos++) {
                ans[xPos][yPos] = count++;
            }
            for (; yPos >= offset; yPos--) {
                ans[xPos][yPos] = count++;
            }
            for (; xPos >= offset; xPos--) {
                ans[xPos][yPos] = count++;
            }
            xPos++;
            yPos++;
            offset++;
        }
        // n 为奇数，赋值最中间值
        if (n % 2 == 1) {
            ans[n / 2][n / 2] = count;
        }
        return ans;
    }
}

数组总结

双指针：
快慢指针（都从一端出发，一快一慢）——我用 slow、fast
左右指针（两边向中间聚拢）——我用 left、right

滑动窗口模板：
待补充

注意：数组有 负数 的情况，不能用滑动窗口
因为有负数的话无论你收缩还是扩张窗口，你里面的值的总和都可能增加或减少