2022“杭电杯”中国大学生算法设计超级联赛（1）补题

已于 2022-07-20 20:51:50 修改
阅读量564 收藏
点赞数 2
CC 4.0 BY-SA版权
文章标签： 算法 c++
于 2022-07-20 00:18:44 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/TroyeJscom/article/details/125883698
本文介绍了几个算法设计问题，包括基于概率的删除操作求期望、数字分堆游戏、背包问题、最短路径优化和激光武器路径规划。通过深入分析题意和巧妙的数学建模，给出了高效的解决方案，涉及到了概率计算、动态规划和图论等算法思想。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

2022“杭电杯”中国大学生算法设计超级联赛（1）

[题目链接](Search Result (hdu.edu.cn))

K Random

题目大意

在[0,1]中随机取N个数字，进行M次操作。对于每次操作，有一半的概率删除最大值，一半的概率删除最小值。问剩余数字的和的期望值（mod109+7）。

题解

易得，剩余的数字分布一定关于0.5对称，所以就是剩余的数字的个数(n-m)除以2，即乘以2的逆元(109+7)。

代码

#include <iostream>
#include <cmath>
using namespace std;
typedef long long ll;
ll n, m, mod = 1e9 + 7;
ll qpow(ll a, ll n, ll mod)
{
    ll res = 1;
    while (n)
    {
        if (n & 1)
            res = (res * a) % mod;
        a = (a * a) % mod;
        n >>= 1;
    }
    return res;
}
ll inv(ll a, ll p)
{
    return qpow(a, p - 2, p);
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    ll t;
    cin >> t;
    ll ni = inv(2, mod);
    while (t--)
    {
        cin >> n >> m;
        cout << ((n - m) * ni) % mod << endl;
    }
    return 0;
}

L Alice and Bob

题目大意

Alice和Bob玩游戏，有m个数字，数字都在0-n之间，游戏规则如下：

Alice可以把数字任意分成两堆，Bob可以把这两堆数字删除一堆，并且另一堆数字都减一。

如果有0出现，Alice赢，否则Bob赢。

题解

Alice的操作，对于一个数字i，有ai个，每次将i平分到两堆数字中，Bob删掉其中一堆，另一堆的每个i都会减一。若到i变为0后，ai仍然不为零，即Alice赢；否则Bob赢。

代码

#include <iostream>
using namespace std;
const int maxn = 1e6 + 5;
int n, t;
int a[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> t;
    while (t--)
    {
        cin >> n;
        for (int i = 0; i <= n; i++)
            cin >> a[i];
        for (int i = n; i > 0; i--)
            a[i - 1] += a[i] / 2;
        if (a[0])
            cout << "Alice" << endl;
        else
            cout << "Bob" << endl;
    }
    return 0;
}

C Backpack

题目大意

Alice有一个容量为m的背包。

现在有n件物品，每一个物品有体积vi和价值wi。

问这n件物品是否可以把背包装满，如果可以，输出装入背包的物品的价值的最大异或和，否则输出-1。

题解

因为wi小于210(1024)，所以wi的异或和不可能超过1024；且m小于210，所以只需要存储容量不超过m的情况下的结果即可。因此可以定义两个bitset<1050>数组f和g来实现，其中f表示当前的情况，g暂时存储对f数组值的操作。

f[i]数组存储价值异或和为i的容积情况，即假如f[2]等于10010，表示价值异或和为2时，容积可以为1和4；f[0]等于00001，表示价值异或和为0时，容积为0。

初始化f[0] [0] = 1，表示一个物品都未添加时，价值的异或和为0，容积为0。

当添加商品i时，g[i]存储的是价值异或和为i^wi，容积添加vi以后的容积。此时f[i]等于以前的异或和为i的情况|(或)上现在的异或和为i的情况。

g[i]的i此时实际是i异或w，f[i]所要找的为，w异或x=i的g[x]，x=i异或w（a异或b等于c，则a异或c等于b）。

最后判断所有的f[i]，若其第m位为1，说明有该种结果，否则没有。

表达可能比较混乱。

小tip(提交语言使用G++)

代码

#include <iostream>
#include <bitset>
using namespace std;
const int Size = 1024;
int n, m, t, v, w, res;
bitset<1050> f[1050], g[1050];
int main()
{
    scanf("%d", &t);
    while (t--)
    {
        scanf("%d%d", &n, &m);
        for (int i = 0; i < Size; i++)
        {
            f[i].reset();
        }
        f[0][0] = 1;
        for (int i = 1; i <= n; i++)
        {
            scanf("%d%d", &v, &w);
            for (int j = 0; j < Size; j++)
            {
                g[j] = f[j];
                g[j] <<= v;
            }
            for (int j = 0; j < Size; j++)
            {
                f[j] |= g[j ^ w];
            }
        }
        res = -1;
        for (int i = 0; i < Size; i++)
        {
            if (f[i][m])
                res = i;
        }
        printf("%d\n", res);
    }
    return 0;
}

B Dragon slayer

题目大意

英雄需要到龙所在的地方拯救公主。已知地图的左下角是(0,0)，右上角是(n,m)，英雄坐标(xs+0.5,ys+0.5)，龙坐标(xt+0.5,yt+0.5)，英雄可以向任意方向走。在地图中有一些水平或垂直的墙，英雄不能穿过这些墙（包括边界），但是英雄可以击破这些墙。问英雄到达龙的位置需要击破的最少的墙。

题解

大佬讲解链接

参考了大佬的题解。

因为墙的数量最大为15，可以使用状态压缩，枚举所有情况。

英雄和龙的坐标(+0.5,+0.5)意思是他们在方格正中间。因为墙只有水平和垂直的，所以可以只看英雄是否可以到他的邻近的上下左右四个格子即可。如下图。

该图为判断左边的黑点是否可以到达右边的黑点，只需要判断两点之间是否有墙（即图中黑色的线）。可以将两个点都向左下移动（图中绿色的点），然后将左边的点按紫色的线移动到新的位置，此时只需判断是否有墙的坐标满足以下条件，wall[i].y <= y1（靠下的绿点） && wall[i].yy >= y2（靠上的绿点）。

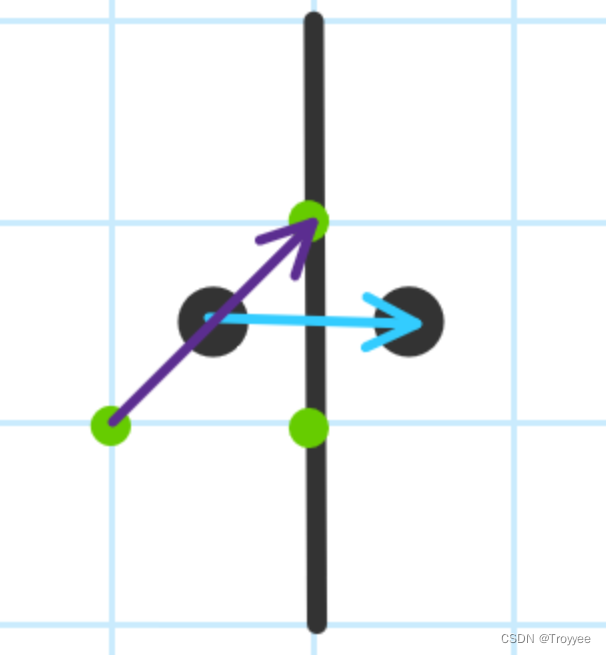
在这里插入图片描述

其余方向可以类似变化。

向上移动

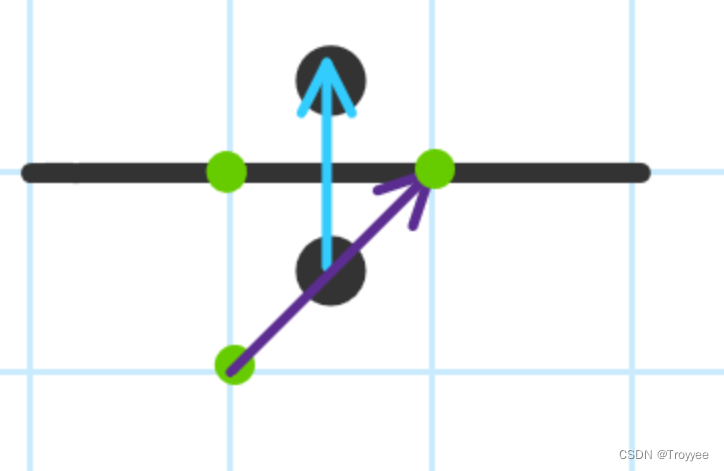
在这里插入图片描述

向左移动

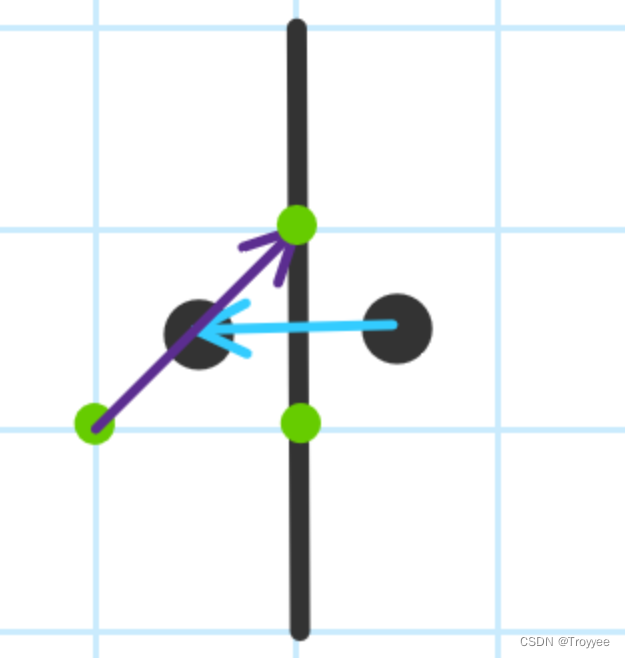
在这里插入图片描述

向下移动

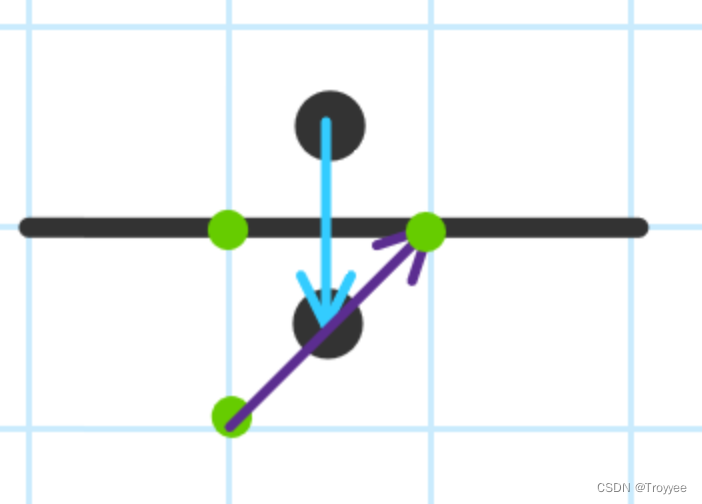
在这里插入图片描述

总之就是，要把两绿点中不在“墙”上的一点移动到“墙”上，以判断是否有墙满足条件，若有，则说明英雄在该点无法向此方向移动。

代码

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
typedef pair<int, int> P;
int n, m, k, sx, sy, tx, ty, t, res;
bool vis1[20], vis2[20][20];
int dx[] = {1, -1, 0, 0}, dy[] = {0, 0, 1, -1};
struct Wall
{
    int x, y, xx, yy;
} wall[20];
int getnum(int state)
{
    memset(vis1, 0, sizeof vis1);
    int ans = 0, in = 1;
    while (state)
    {
        if (state & 1)
        {
            ans++;
            vis1[in] = 1;
        }
        in++;
        state >>= 1;
    }
    return ans;
}
bool checkWall(int x1, int y1, int x2, int y2)
{
    for (int i = 1; i <= k; i++)
    {
        if (vis1[i])
            continue;
        if (x1 == x2 && wall[i].x == wall[i].xx && x1 == wall[i].x && wall[i].y <= y1 && wall[i].yy >= y2)
            return 0;
        if (y1 == y2 && wall[i].y == wall[i].yy && y1 == wall[i].y && wall[i].x <= x1 && wall[i].xx >= x2)
            return 0;
    }
    return 1;
}
bool bfs()
{
    memset(vis2, 0, sizeof vis2);
    queue<P> q;
    q.push(make_pair(sx, sy));
    vis2[sx][sy] = 1;
    while (q.size())
    {
        P now = q.front();
        q.pop();
        for (int i = 0; i < 4; i++)
        {
            int nx = now.first + dx[i], ny = now.second + dy[i];
            if (nx < 0 || nx == n || ny < 0 || ny == m || vis2[nx][ny])
                continue;
            if ((i == 0 || i == 2) && checkWall(nx, ny, now.first + 1, now.second + 1))
            {
                if (nx == tx && ny == ty)
                    return 1;
                vis2[nx][ny] = 1;
                q.push(make_pair(nx, ny));
            }
            if ((i == 1 || i == 3) && checkWall(now.first, now.second, nx + 1, ny + 1))
            {
                if (nx == tx && ny == ty)
                    return 1;
                vis2[nx][ny] = 1;
                q.push(make_pair(nx, ny));
            }
        }
    }
    return 0;
}
int main()
{
    scanf("%d", &t);
    while (t--)
    {
        res = 0x3f3f3f3f;
        scanf("%d%d%d%d%d%d%d", &n, &m, &k, &sx, &sy, &tx, &ty);
        for (int i = 1; i <= k; i++)
            scanf("%d%d%d%d", &wall[i].x, &wall[i].y, &wall[i].xx, &wall[i].yy);
        for (int i = 0; i < (1 << k); i++)
        {
            int cnt = getnum(i);
            if (cnt >= res)
                continue;
            if (bfs())
                res = cnt;
        }
        printf("%d\n", res);
    }
    return 0;
}

I Laser

题目大意

一个二维平面，一共有n个敌人，第i个敌人的位置是(xi,yi)。现在有一个激光武器，你可以把它放在任意(x,y)(x, y 是实数)上，对于任何实数 k，坐标为 (x+k, y),(x,y+k),(x+k,y+k),(x+k,y−k)的敌人将被消灭，即“米”字。问是否有可能消灭所有敌人。

题解

先选取两个不在同一条线（指横竖斜）的点，对每一个点作四条直线，交出十二个点，只需判断这十二个点是否至少有一个满足条件，因为答案肯定出现在这十二个点中（因为肯定需要满足扫到这两个“不共线”的点）。

这十二个点需要一个个去判断是否能消灭其他点。

具体步骤：以第一个点为一个基点遍历其他点，若没找到“不共线”的点，则说明在第一个点放置武器即可，否则，以找到的第一个“不共线”的点为第二个基点，进行上述过程。

代码

#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
const int maxn = 5e5 + 5;
int t, n;
int x[maxn], y[maxn];
int tx, ty;
bool flag;
bool check(int x, int y)
{
    if (x == 0 || y == 0 || x == y || x + y == 0)
        return 1;
    return 0;
}
int main()
{
    scanf("%d", &t);
    while (t--)
    {
        scanf("%d", &n);
        for (int i = 1; i <= n; i++)
            scanf("%d%d", &x[i], &y[i]);
        flag = 1;
        for (int i = 2; i <= n; i++)
        {
            if (!check(x[1] - x[i], y[1] - y[i]))
            {
                flag = 0;
                tx = x[i], ty = y[i];
                break;
            }
        }
        if (flag)
            printf("YES\n");
        else
        {
            vector<pair<int, int>> v;
            v.emplace_back(x[1], ty + tx - x[1]);
            v.emplace_back(x[1], ty);
            v.emplace_back(x[1], x[1] - tx + ty);
            v.emplace_back(tx - ty + y[1], y[1]);
            v.emplace_back(tx, y[1]);
            v.emplace_back(tx + ty - y[1], y[1]);
            v.emplace_back(tx, tx - x[1] + y[1]);
            v.emplace_back(x[1] + ty - y[1], ty);
            v.emplace_back(x[1] - ty + y[1], ty);
            v.emplace_back(tx, y[1] - tx + x[1]);
            v.emplace_back((tx + x[1] + ty - y[1]) / 2, (tx - x[1] + y[1] + ty) / 2);
            v.emplace_back((x[1] - ty + y[1] + tx) / 2, (ty + y[1] - tx + x[1]) / 2);
            for (int i = 0; i < 12; i++)
            {
                flag = 1;
                int dx = v[i].first, dy = v[i].second;
                for (int j = 2; j <= n; j++)
                {
                    if (!check(dx - x[j], dy - y[j]))
                    {
                        flag = 0;
                        break;
                    }
                }
                if (flag)
                    break;
            }
            if (flag)
                printf("YES\n");
            else
                printf("NO\n");
        }
    }
    return 0;
}

D Ball

题目大意

在一个M*M的棋盘上有N个点，如果某三个点之间的距离的中位数是质数则算满足条件，问有几对满足条件。

题解

首先需要判断出一个数是不是质数，可以使用埃氏筛预处理。

然后考虑枚举一下三个点，可以分别计算距离并进行判断，但这样子时间复杂度太高，所以考虑枚举两个点，即算出所有的边。

最后是确定第三个点，要求其中一条边小于等于这条边，另一条边大于等于这条边，即这条边就是中间的边。

具体实现：将所有的边从小到大排序，然后从前往后遍历，如果该边的长度为质数，则根据bitset数组s计算结果，然后标记一些数据；否则，只标记数据。

bitset数组s存储信息：因为从小到大遍历边，所以s[i] [j]为1表示从i点到j点有一条边，该边小于等于当前循环的边（之前的循环标记的），s[i] [j]为0表示从i点到j点有一条边，该边大于等于当前循环的边（之前的循环未标记）。

s[edge[i].a] ^ s[edge[i].b]，对于每一位有四种情况。00，说明a到c和b到c的边都大于该边（如果等于，会在后面计算，不会遗漏，后面同），不满足，为0；01和10，说明a到c和b到c的边一个大于该边，一个小于该边，满足，为1；11，说明a到c和b到c的边都小于该边，不满足，为0。所以计算s[edge[i].a] ^ s[edge[i].b]中1的个数即可。

代码

#include <iostream>
#include <cmath>
#include <algorithm>
#include <bitset>
using namespace std;
const int maxn = 2e3 + 5;
const int maxm = 2e5 + 5;
int n, m, t, cnt;
long long res;
bool isnp[maxm];
bitset<maxn> s[maxn];
struct Point
{
    int x, y;
} point[maxn];
struct Edge
{
    int dis, a, b;
    Edge(int dis = 0, int a = 0, int b = 0) : dis(dis), a(a), b(b) {}
    bool operator<(const Edge &a) const
    {
        return dis < a.dis;
    }
} edge[maxn * maxn];
void init(int n)
{
    isnp[1] = 1;
    for (int i = 2; i * i <= n; i++)
    {
        if (!isnp[i])
        {
            for (int j = i * i; j <= n; j += i)
                isnp[j] = 1;
        }
    }
}
int main()
{
    init(200000);
    scanf("%d", &t);
    while (t--)
    {
        cnt = res = 0;
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++)
            s[i].reset();
        for (int i = 1; i <= n; i++)
            scanf("%d%d", &point[i].x, &point[i].y);
        for (int i = 1; i <= n; i++)
        {
            for (int j = i + 1; j <= n; j++)
            {
                edge[++cnt] = Edge(abs(point[i].x - point[j].x) + abs(point[i].y - point[j].y), i, j);
            }
        }
        sort(edge + 1, edge + cnt + 1);
        for (int i = 1; i <= cnt; i++)
        {
            if (!isnp[edge[i].dis])
            {
                res += (s[edge[i].a] ^ s[edge[i].b]).count();
            }
            s[edge[i].a][edge[i].b] = 1;
            s[edge[i].b][edge[i].a] = 1;
        }
        printf("%lld\n", res);
    }
    return 0;
}

若有理解不对的地方，多多包含。

Troyyee
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值