TensorFlow

TensorFlow介绍

  TensorFlow是一个采用数据流图（data flow graphs），用于数值计算的开源软件库。节点（Nodes）在图中表示数学操作，图中的线（edges）则表示在节点间相互联系的张量（tensor），可以把计算图看做是一种有向图，张量从图中流过的直观图像是这个工具取名为“Tensorflow”的原因。TensorFlow更灵活的一点你可以指定各个节点在哪个具体的设备上运行，如CPU和GPU，一旦输入端的所有张量准备好，节点将被分配到各种计算设备完成异步并行运算任务。
  Tensorflow通过Graph和Session的设定，对神经网络模型进行了三重解构，第一层解构是将数据与神经网络模型进行了分离，所以要先设计神经网络模型，再导入数据进行训练，从而得出神经网络节点参数。第二层解构是通Graph将神经网络模型进行结构化分区，通过结构化分区把复杂的神经网络进行了解构，研究人员可以按Graph的结果对特定的神经网络模型组成部分进行局部微调，通过局部微调实现全局复杂神经网络的组建。第三层次的解构就是通过Session的设计，将神经网络的运算拆解到相关的算力中心，这就导致大规模的算力组合训练复杂的人工神经网络模型成为了可能性。

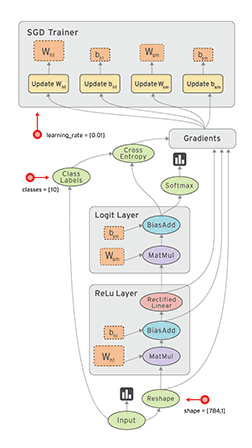
Tensorflow中的概念

Tensorflow中最重要的几个概念：

  图（Graph）：Tensorflow就是建立数据流图来进行数值计算。它包含了一个计算任务中的所有变量和计算方式。所以，使用Tensorflow来搭建模型时，其实主要涉及两个方面：根据模型建立计算图，然后送入数据运行计算图得到结果。计算图是Tensorflow中很重要的一个概念，其是由一系列节点（nodes）组成的图模型，每个节点对应的是Tensorflow的一个算子（operation）。每个算子会有输入与输出，并且输入和输出都是张量。做一个机器学习的任务就是计算一张图，在计算图之前，需要把图建立好。这个计算图是静态的，即这个计算图每个节点接收什么样的张量和输出什么样的张量已经固定下来。
  Tensorflow中的节点变量是可以被递归的更新的。所说的“训练”，也就是不停的计算一个图，获得图的计算结果，再根据结果的值调整节点变量的值，然后根据新的变量的值再重新计算图，如此重复，直到结果令人满意（小于某个阈值）。

会话（Session）：要运行一个计算图，需要开启一个会话（session），在session中这个计算图才可以真正运行。
Runner：在建立图之后，必须使用会话中的Runner来运行图，才能得到结果。在运行图时，需要为所有的变量和占位符赋值，否则就会报错。

  张量（tensor）: Tensorflow中所有的输入输出变量都是张量，而不是基本的int，double这样的类型，即使是一个整数1，也必须被包装成一个0维的，长度为1的张量【1】。一个张量和一个矩阵差不多，可以被看成是一个多维的数组，从最基本的一维到N维都可以。张量拥有阶（rank），形状（shape），和数据类型。其中，形状可以被理解为长度，例如，一个形状为2的张量就是一个长度为2的一维数组。而阶可以被理解为维数。

阶	数学实例	Python 例子
0	纯量 (只有大小)	s = 483
1	向量(大小和方向)	v = [1.1, 2.2, 3.3]
2	矩阵(数据表)	m = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
3	3阶张量 (数据立体)	t = [[[2], [4], [6]], [[8], [10], [12]], [[14], [16], [18]]]

对于任何深度学习框架，你都要先了解张量（Tensor）的概念，张量可以看成是向量和矩阵的衍生。向量是一维的，而矩阵是二维的，对于张量其可以是任何维度的。一般情况下，你要懂得张量的两个属性：形状（shape）和秩（rank）。秩很好理解，就是有多少个维度；而形状是指的每个维度的大小。下面是常见的张量的形象图表示：

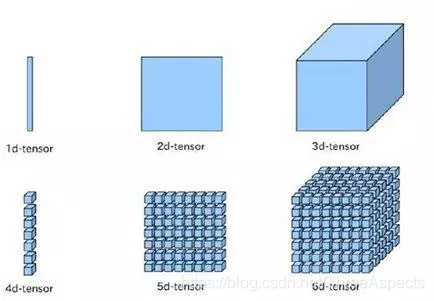
名字就是TensorFlow，直观来看，就是张量的流动。张量(tensor)，即任意维度的数据，一维、二维、三维、四维等数据统称为张量。而张量的流动则是指保持计算节点不变，让数据进行流动。这样的设计是针对连接式的机器学习算法，比如逻辑斯底回归，神经网络等。连接式的机器学习算法可以把算法表达成一张图，张量从图中从前到后走一遍就完成了前向运算；而残差从后往前走一遍，就完成了后向传播。

TensorflowSharp中的几类主要变量

• Const：常量，这很好理解。它们在定义时就必须被赋值，而且值永远无法被改变
• Placeholder：占位符。这是一个在定义时不需要赋值，但在使用之前必须赋值（feed）的变量，通常用作训练数据
• Variable：变量，它和占位符的不同是它在定义时需要赋值，而且它的数值是可以在图的计算过程中随时改变的。因此，占位符通常用作图的输入（即训练数据），而变量用作图中可以被“训练”或“学习”的那些tensor，例如y=ax+b中的a和b

深度模型训练方法

  深度学习模型的训练是一个迭代的过程，在每一轮迭代过程中，前向传播算法会根据当前参数的取值，计算出在一小部分训练数据上的预测值，然后反向传播算法，再根据损失函数计算参数的梯度并且更新参数。

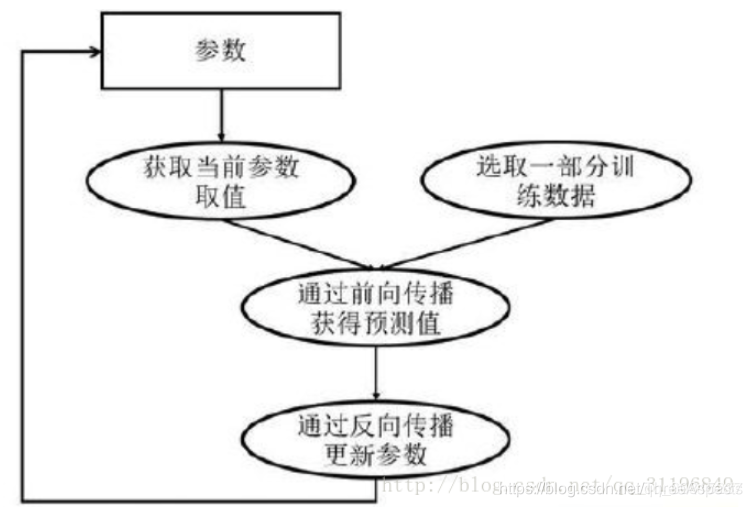
训练方法

1. 在异步模式下在并行化地训练深度学习模型时，不同设备（GPU或CPU）可以在不同训练数据上，运行整个迭代的过程
2. 在同步模式下，所有的设备同时读取参数的取值，并且当反向传播算法完成之后同步更新参数的取值，单个设备不会单独对参数进行更新，而会等所有设备都完成反向传播之后再统一更新参数

异步模式训练流程：

• 在每一轮迭代时，不同设备会读取参数最新的取值
• 因为设备不同，读取参数取值时间不一样，所以得到的值也可能不一样
• 根据当前参数的取值，和随机获取的一小部分训练数据，不同设备各自运行反向传播的过程，并且独立地更新参数
• 可以认为异步模式，就是单机模式复制了多份，每一份使用不同的训练数据进行训练。
• 在异步模式下，不同设备之前是完全独立的

同步模式训练流程：

• 图中在迭代每一轮时，不同设备统一读取当前参数的取值，并随机获取一小部分数据
• 然后在不同设备上运行反向传播过程得到在各自训练数据上的参数的梯度 ，虽然所有设备使用的参数是一致的，但是因为训练数据不同，所以得到的参数的梯度可能不一样
• 当所有设备完成反向传播的计算之后，需要计算出不同设备上参数梯度的平均值
• 最后再根据平均值对参数进行更新

  在同步更新的时候， 每次梯度更新，要等所有分发出去的数据计算完成后，返回回来结果之后，把梯度累加算了均值之后，再更新参数。 这样的好处是loss的下降比较稳定， 但是这个的坏处也很明显， 处理的速度取决于最慢的那个分片计算的时间。
  在异步更新的时候， 所有的计算节点，各自算自己的， 更新参数也是自己更新自己计算的结果， 这样的优点就是计算速度快， 计算资源能得到充分利用，但是缺点是loss的下降不稳定， 抖动大。
  在数据量小的情况下， 各个节点的计算能力比较均衡的情况下， 推荐使用同步模式；数据量很大，各个机器的计算性能掺差不齐的情况下，推荐使用异步的方式。

手写DNN

手写DNN的计算过程：

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
 
#使用numpy生成200个随机点
x_data=np.linspace(-0.5,0.5,200)[:,np.newaxis]
noise=np.random.normal(0,0.02,x_data.shape)
y_data=np.square(x_data)+noise
 
#定义两个placeholder存放输入数据
x=tf.placeholder(tf.float32,[None,1])
y=tf.placeholder(tf.float32,[None,1])
 
#定义神经网络中间层
Weights_L1=tf.Variable(tf.random_normal([1,10]))
biases_L1=tf.Variable(tf.zeros([1,10]))    #加入偏置项
Wx_plus_b_L1=tf.matmul(x,Weights_L1)+biases_L1
L1=tf.nn.tanh(Wx_plus_b_L1)   #加入激活函数
 
#定义神经网络输出层
Weights_L2=tf.Variable(tf.random_normal([10,1]))
biases_L2=tf.Variable(tf.zeros([1,1]))  #加入偏置项
Wx_plus_b_L2=tf.matmul(L1,Weights_L2)+biases_L2
prediction=tf.nn.tanh(Wx_plus_b_L2)   #加入激活函数
 
#定义损失函数
loss=tf.reduce_mean(tf.square(y-prediction))
#定义反向传播算法（使用梯度下降算法训练）
train_step=tf.train.GradientDescentOptimizer(0.1).minimize(loss)
 
with tf.Session() as sess:
    #变量初始化
    sess.run(tf.global_variables_initializer())
    #训练2000次
    for i in range(2000):
        sess.run(train_step,feed_dict={x:x_data,y:y_data})
 
    #获得预测值
    prediction_value=sess.run(prediction,feed_dict={x:x_data})
 
    #画图
    plt.figure()
    plt.scatter(x_data,y_data)   #散点是真实值
    plt.plot(x_data,prediction_value,'r-',lw=5)   #曲线是预测值
    plt.show()

写一个DNN实现手写数字识别：

reset_graph()
 
n_inputs = 28 * 28  # MNIST
n_hidden1 = 300 # reused
n_hidden2 = 50  # reused
n_hidden3 = 50  # reused
n_hidden4 = 20  # new!
n_outputs = 10  # new!
 
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
 
with tf.name_scope("dnn"):
    hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1")       # reused
    hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, name="hidden2") # reused
    hidden3 = tf.layers.dense(hidden2, n_hidden3, activation=tf.nn.relu, name="hidden3") # reused
    hidden4 = tf.layers.dense(hidden3, n_hidden4, activation=tf.nn.relu, name="hidden4") # new!
    logits = tf.layers.dense(hidden4, n_outputs, name="outputs")                         # new!
 
with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")
 
with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
 
with tf.name_scope("train"):
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss)
    
#创建一个restore_saver来恢复预训练模型（为其提供要恢复的变量列表，否则它会抱怨图形不匹配）    
reuse_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES,
                               scope="hidden[123]") # regular expression
restore_saver = tf.train.Saver(reuse_vars) # to restore layers 1-3
 
init = tf.global_variables_initializer()
saver = tf.train.Saver()
 
with tf.Session() as sess:
    init.run()
    restore_saver.restore(sess, "./my_model_final.ckpt")
 
    for epoch in range(n_epochs):                                            # not shown in the book
        for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size): # not shown
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch})        # not shown
        accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})     # not shown
        print(epoch, "Validation accuracy:", accuracy_val)                   # not shown
 
    save_path = saver.save(sess, "./my_new_model_final.ckpt")

写一个CNN实现手写数字识别：

import tensorflow as tf
import numpy as np
 
height=28
width=28
channels = 1
n_inputs = height * width
 
conv1_fmaps = 32  #卷积核个数
conv1_ksize = 3   #卷积核宽高
conv1_stride = 1  #步幅
conv1_pad = "SAME"
 
conv2_fmaps = 64
conv2_ksize = 3
conv2_stride = 2
conv2_pad = "SAME"
 
pool3_fmaps = 64
 
n_fc1 = 64
n_outputs = 10
 
 
reset_graph()
with tf.name_scope("inputs"):
    X=tf.placeholder(tf.float32,shape=[None,n_inputs],name="X")
    X_reshaped=tf.reshape(X,shape=[-1,height,width,channels])
    y=tf.placeholder(tf.int32,shape=[None],name="y")
 
conv1 = tf.layers.conv2d(X_reshaped, filters=conv1_fmaps, kernel_size=conv1_ksize,
                         strides=conv1_stride, padding=conv1_pad,
                         activation=tf.nn.relu, name="conv1")
conv2 = tf.layers.conv2d(conv1, filters=conv2_fmaps, kernel_size=conv2_ksize,
                         strides=conv2_stride, padding=conv2_pad,
                         activation=tf.nn.relu, name="conv2")
with tf.name_scope("pool3"):
    pool3=tf.nn.max_pool(conv2,ksize=[1,2,2,1],strides=[1,2,2,1],padding="VALID")
    pool3_flat=tf.reshape(pool3,shape=[-1,pool3_fmaps*7*7])     #卷积核个数*7*7，池化之后要把二维图像转化为一维列向量
 
with tf.name_scope("fc1"):
    fc1=tf.layers.dense(pool3_flat,n_fc1,activation=tf.nn.relu,name="fc1")#全链接，每个特征图的一维列向量均与64个神经元相连
    
with tf.name_scope("output"):
    logits=tf.layers.dense(fc1,n_outputs,name="output")
    Y_proba=tf.nn.softmax(logits,name="Y_proba")
 
 
with tf.name_scope("train"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=y)# 损失函数：计算交叉熵
    loss = tf.reduce_mean(xentropy)   #平均交叉熵
    optimizer = tf.train.AdamOptimizer()
    training_op = optimizer.minimize(loss)
 
with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
 
with tf.name_scope("init_and_save"):
    init = tf.global_variables_initializer()
    saver = tf.train.Saver()
 
 
def shuffle_batch(X, y, batch_size):
    rnd_idx = np.random.permutation(len(X))
    n_batches = len(X) // batch_size
    for batch_idx in np.array_split(rnd_idx, n_batches):
        X_batch, y_batch = X[batch_idx], y[batch_idx]
        yield X_batch, y_batch
 
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.astype(np.float32).reshape(-1, 28*28) / 255.0
X_test = X_test.astype(np.float32).reshape(-1, 28*28) / 255.0
y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
X_valid, X_train = X_train[:5000], X_train[5000:]
y_valid, y_train = y_train[:5000], y_train[5000:]
 
n_epochs = 10
batch_size = 100
 
with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
        acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test})