ALS

Spark MLlib

  MLlib目前支持4种常见的机器学习问题：分类、回归、聚类和协同过滤。spark.mllib包含基于RDD的原始算法API。spark.ml 则提供了基于DataFrames 高层次的API，可以用来构建机器学习工作流（PipeLine）。ML Pipeline 弥补了原始 MLlib 库的不足，向用户提供了一个基于 DataFrame 的机器学习工作流式 API 套件。
  利用SparkSQL处理完的数据会分成训练集的数据和测试集的数据（用来验证模型是否是准确的）。ALS中有train方法，会返回MatrixFactorizationModel。MatrixFactorizationModel中很多方法：在得到这个模型以后调用recomendProducts或recomendUsers方法，就能够得到想要的推荐结果。

val model1 = ALS.train(ratings, rank, numIterations, lambda)//显性反馈模型
val model2 = ALS.trainImplicit(ratings, rank, numIterations, lambda, alpha)//隐性反馈模型

参数包括：
ratings：userId、productId、rating的三元组
rank：隐含因子
numIterations：迭代次数
Lambda：正则项的惩罚系数
alpha： 置信参数

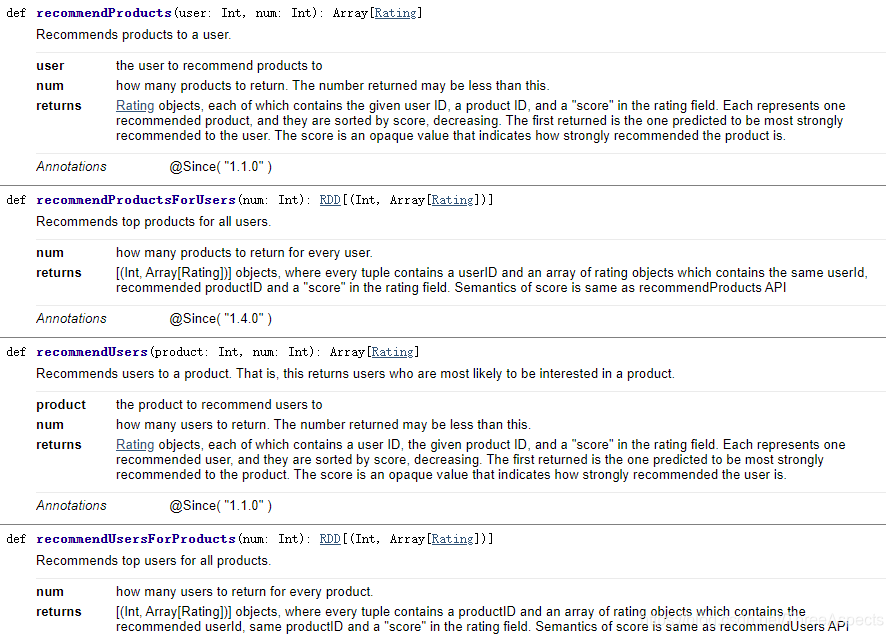
ALS

  ALS（交替最小二乘法），从协同过滤的分类来说，ALS算法属于混合CF，因为它同时考虑了User和Item两个方面，既可基于用户进行推荐又可基于物品进行推荐。用户和商品的关系，可以抽象为如下的三元组：<User,Item,Rating>。
  在spark MLlib 机器学习库中目前推荐模型只包含基于矩阵分解(matrix factorization)的实现。可以将矩阵分解成用户-特征矩阵和物品-特征矩阵。具体的分解思路，找出两个低维的矩阵，使得它们的乘积是原始矩阵。因此矩阵分解相当于进行了特征提取或者数据的降维。
  由于评分数据中有大量的缺失项，传统的矩阵分解SVD（奇异值分解）不方便处理这个问题。该方法在矩阵分解之前需要先把评分矩阵R缺失值补全，补全之后稀疏矩阵R表示成稠密矩阵R’，然后将R’分解成如下形式：R’ = UTSV。这种方法有两个缺点，第一是补全成稠密矩阵之后需要耗费巨大的存储空间，在实际中，用户对物品的行为信息量庞大，对这样的稠密矩阵的存储是不现实的；第二，SVD的计算复杂度很高。
  而ALS能够很好的解决这个问题。对于R(m×n)的矩阵，ALS旨在找到两个低维矩阵X(m×k)和矩阵Y(n×k)，来近似逼近R(m×n)，即：$R_{m\times n}$≈$X_{m\times k}$$Y_{n\times k}^T$ 。其中R(m×n)代表用户对商品的评分矩阵，X(m×k)代表用户对隐含特征的偏好矩阵，Y(n×k)表示商品所包含隐含特征的矩阵。
  为了找到使低秩矩阵X和Y尽可能地逼近R，需要最小化下面的平方误差损失函数：L(X,Y)=$\sum _{u,i}(r_{ui-x_u^T{y}_i}{)}^2$……（1）
其中$x_u$(1×k)表示示用户u的偏好的隐含特征向量，$y_i$(1×k)表示商品i包含的隐含特征向量, $r_{ui}$表示用户u对商品i的评分, 向量$x_u$和$y_i$的内积$x_u^T{y}_i$是用户u对商品i评分的近似。

  损失函数一般需要加入正则化项来避免过拟合等问题，我们使用L2正则化，所以上面的公式改造为：L(X,Y)=$\sum _{u,i}(r_{ui-x_u^T{y}_i}{)}^2+\lambda (|x_u{|}^2+|y_i{|}^2)$……（2）
其中λ是正则化项的系数。到这里，协同过滤就成功转化成了一个优化问题。由于变量$x_u$和$y_i$耦合到一起，这个问题并不好求解，所以我们引入了ALS。

  使用交替最小二乘法（ALS）来最优化损失函数。ALS的实现原理是迭代式求解一系列最小二乘回归问题。也就是说我们可以先固定Y（例如随机初始化X），然后利用公式（2）先求解X，然后固定X，再求解Y，如此交替往复直至收敛，即所谓的交替最小二乘法求解法。具体求解方法说明如下：

• 先固定Y, 将损失函数L(X,Y)对xu求偏导，并令导数=0，得到：$x_u=(Y^{T}Y+\lambda I{)}^{-1}{Y}^T{r}_u$……（3）
• 同理固定X，可得：$y_i=(X^{T}X+\lambda I{)}^{-1}{X}^T{r}_i$……（4）其中$r_{u(1\times n)}$是R的第u行,$r_{i(1\times m)}$是R的第i列， I是k×k的单位矩阵
• 迭代步骤：首先随机初始化Y，利用公式(3)更新得到X，然后利用公式(4)更新Y，直到均方根误差变RMSE化很小或者到达最大迭代次数。
  $R^{\prime }=XY$
  $RMSE=\sqrt{\frac{\sum (R-R^{\prime }{)}^2}{N}}$

如何评价推荐结果好坏？ 通过MSE：

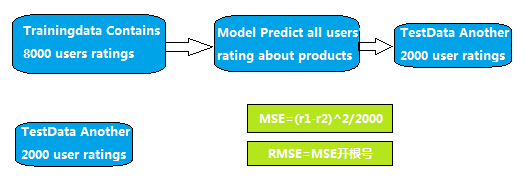
// Evaluate the model on rating data
val usersProducts = ratings.map { case Rating(user, product, rate) =>(user, product)}
val predictions =model.predict(usersProducts).map { case Rating(user, product, rate) =>((user, product), rate)}
val ratesAndPreds = ratings.map { case Rating(user, product, rate) =>((user, product), rate)}.join(predictions)
val MSE = ratesAndPreds.map { 
  case ((user, product), (r1, r2)) =>
  val err = (r1 - r2)
  err * err}.mean()

即得到模型以后会产生一个user和product的tuple，分别为这个tuple得到预测的rating和实际的rating，然后两个rating再转成一个tuple，放到一个函数中做相减。对于推荐结果通过组合迭代的方式，通过变换迭代次数，惩罚值来寻求最佳模型。发现适当增大iterations，减小lambda，均方差可能会减小，从而推荐结果较优

ALS算法的缺点在于：

1. 它是一个离线算法
2. 无法准确评估新加入的用户或商品，即Cold Start（冷启动）问题

隐式反馈
  在实际的电商网站中，存在大量的用户行为间接反映用户的喜好，比如：用户的购买记录、搜索关键字甚至是鼠标的移动。我们将这些间接用户行为称之为隐式反馈（implicit feedback），以区别于评分这样的显式反馈（explicit feedback）。隐式反馈有以下几个特点：

1. 没有负面反馈（negative feedback）。用户一般会直接忽略不喜欢的商品，而不是给予负面评价
2. 隐式反馈包含大量噪声。比如，电视机在某一时间播放某一节目，然而用户已经睡着了，或者忘了换台
3. 显式反馈表现的是用户的喜好（preference），而隐式反馈表现的是用户的信任（confidence）。比如用户最喜欢的一般是电影，但观看时间最长的却是连续剧。大米购买的比较频繁，量也大，但未必是用户最想吃的食物
4. 隐式反馈非常难以量化

val model2 = ALS.trainImplicit(ratings, rank, numIterations, lambda, alpha)//隐性反馈模型

隐式模型多了一个置信参数，这就涉及到ALS中对于隐式反馈模型的处理方式了——有的文章称为“加权的正则化矩阵分解”，它的损失函数如下：
针对隐式反馈，有ALS-WR算法（ALS with Weighted–Regularization）。

• ALS-WR的目标函数：min($x_u,y_i$)L(X,Y)=$\sum _{u,i}{c}_{ui}(p_{ui-x_u^T{y}_i}{)}^2+\lambda (|x_u{|}^2+|y_i{|}^2)$……（5），

我们知道，在隐反馈模型中是没有评分的，所以在式子中rui被pui所取代，pui是偏好的表示，仅仅表示用户和物品之间有没有交互，而不表示评分高低或者喜好程度。比如用户和物品之间有交互就让pui等于1，没有就等于0。
$$\begin{array}{r}{p}_{ui}=1|if:r_{ui}>0\\ p_{ui}=0|if:r_{ui}=0\end{array}$$
函数中还有一个cui的项，它用来表示用户偏爱某个商品的置信程度，比如交互次数多的权重就会增加。如果我们用dui来表示交互次数的话，那么就可以把置信程度表示成如下公式：$c_{ui}=1+\alpha d_{ui}$其中α是置信度系数。

• 求解方式还是最小二乘法：$x_u=(Y^T{C}^{u}Y+\lambda I{)}^{-1}{Y}^T{C}^u{r}_u$……（6），$y_i=(X^T{C}^{i}X+\lambda I{)}^{-1}{X}^T{C}^i{r}_i$……（7）

implicitPrefs 决定了是用显性反馈ALS的版本还是用适用隐性反馈数据集的版本。
alpha 是一个针对于隐性反馈 ALS 版本的参数，这个参数决定了偏好行为强度的基准。

本质上，这个方法将数据作为二元偏好值和偏好强度的一个结合，而不是对评分矩阵直接进行建模。因此，评价就不是与用户对商品的显性评分而是和所观察到的用户偏好强度关联了起来。然后，这个模型将尝试找到隐语义因子来预估一个用户对一个商品的偏好。

参考论文：
《Large-scale Parallel Collaborative Filtering forthe Netflix Prize》
《Collaborative Filtering for Implicit Feedback Datasets》
《Matrix Factorization Techniques for Recommender Systems》

1、隐式数据的使用，系统中存在浏览、点击、播放、关注、分享、购买等数据，怎样同时使用？
最开始的时候，只使用了点击数据，但是产品初期数据量有点小；同时关注、购买数确实相对于点击数据更为重要，因此当前采用这种赋权方法：
value = 5* 购买 + 4* 关注 + 3* 分享 + 2* 播放 + 1*点击

2、spark als怎样使用隐式反馈数据？

ALS als = new ALS()
.setMaxIter(alsIterCount)
.setAlpha(3)
.setRank(50)
.setRegParam(0.01)
.setUserCol("userIdIndex")
.setItemCol("itemId")
.setRatingCol("rating")
.setImplicitPrefs(true);

有三点：

1. rating是一个上面的value，比如点击数目的累加和
2. 加上setImplicitPrefs(true)
3. 加上setAlpha(3)，这个值可以自己调参；不要直接选40(论文中数字)，项目数据如果很少，大于40直接数据就没了

3、对数据的清洗包括哪些
过滤掉userId、itemId为空的数据

4、ALS能否用于相关推荐、相似推荐
ALS没有原生支持，但是可以获取itemFactors，然后自己做crossjoin笛卡尔乘积，然后计算item和item之间的相似度，获取TOP K个最相关的即可

5、ALS计算结果怎么使用
当前只计算了相关推荐；以item为KEY，以itemlist为value存入了REDIS；前端每次访问直接根据itemId取出itemlist即可返回，几十毫秒即可；由于item变动不频繁，所以每天计算一次

6、怎么处理冷启动
对于新加入物品，直接取对应分类的热门列表即可；第二天就有了用户行为数据