Vamei博客学习笔记（6）

本文取自：

1. 统计01：概述
2. 统计02：怎样描绘数据
3. 绘图: matplotlib核心剖析
4. 线性代数01 线性的大脑
5. 信号与频谱

• 统计的历史

  “统计”英文是statistics，词根就源于state，也就是“国家”。统计方法作为整理和描述数据的手段，变得不可或缺。

  • 政府

    政府必须搜刮到足够多的税收，才能弥补国库亏空。“统计”因此成了君王不可或缺的工具

  • 学术

    对于伽利略和培根这样的科学家来说，实验产生的数据是科学的唯一基石。

  到了二十世纪初，概率论完成了理论体系的建设，统计学家才看到严格化统计学的希望。

  统计学家把抽样理解为概率论中的“随机事件”，从而在概率论和统计之间建立了桥梁。

• 群体(population)

  统计研究的对象是某个群体(population)。群体包括了与问题相关的所有个体。

  收集群体中所有个体的数据，是了解一个群体最完备的方法。但人脑存储和处理信息的能力有限，因此往往看不了几行就会头晕脑胀。

  我们需要描述群体数据的办法。

• 描述数据的方法

  1. 画图

     画图可以把数字信息变得几何化，从而让统计数据变得容易理解。

  2. 计算群体参数(population parameter)

     比如群体的平均值和方差。这些参数用一个单一数字来代表群体某一方面的信息。

• 统计推断(statistical inference)

  用样本来推测群体的信息。被称为统计推断(statistical inference)。

  1. 群体

     最好的办法是获取群体数据，但效率较低，有时候也不可能。故而转为抽样

  2. 抽样(sampling)

     繁华如三千东流水，我只取一瓢饮。

     把抽样看作一个随机事件，是统计向概率论靠拢的关键。

     建立在样品之上，还有一个简单而重要的概念，就是样品统计量(sample static)

  3. 不确定性量化

     抽样存在随机性，其中的不确定性需要被量化。

数据描述就是要用一定的方法来提取少量信息，从而让人更容易明白数据的含义。

数据描述的方法可以分为两大门类，即群体参数和数据绘图。

• 群体参数

  群体参数是用一些数字来表示群体的特征。

  1. 群体平均值（population mean）反映群体总体状况

  2. 群体方差（population variance）反映群体的离散状况

  3. 群体标准差（standard deviation）

     从物理的角度上来看，平均值和标准差所带的单位，都和原始数据相同。

     在多数统计案例中，大部分的群体数据会落在平均值加减一个标准差的范围内。

  4. 最大值（max）和最小值（min）,需要经过排序才能知道

  5. 中位数（median）：如果群体总数为偶数，那么中位数就是中间两个成员取值的平均值

  6. 四分位数（quartile）：对平分后的数据再取中位数

     1. 下四分位数（lower quartile）
     2. 上四分位数（upper quartile）

  7. 四分位距（IQR，inter quartile range）
     $$\begin{gathered} Q1=lowerquartile \\ Q2=M=median \\ Q3=upperquartile \\ IQR=Q3-Q1 \end{gathered}$$
     中位数和四分位数都属于百分位数（percentile），把数据按数值大小排列，处于p%位置的成员的取值，称第p百分位数。

• 数据绘图

  数据绘图利用了人类对形状的敏感。在通过数据绘图，我们可以将数字转换的几何图形，让数据中的信息变得更容易消化。经典的绘图只有那么几种，如饼图、散点图、曲线图。

  1. 饼图 （pie plot）plt.pie() 呈现比例，无法表达具体取值
  2. 条形图（bar plot）呈现具体取值
  3. 直方图（histogram），条形图的进化版，自动处理更能呈现出一些数据特征
  4. 趋势图（run chart）又称为折线图，经常用于呈现时间序列。从视觉上体现出数据随时间变化的特征。
  5. 散点图（scatter plot）是一种最直接的表达二维关系的绘图方式。二维绘图的其他方式，都可以理解成散点图的一个变种。
  6. 泡泡图（bubble plot），进化版散点图，用三点大小表示第三维数据
  7. 箱形图（box plot），侧重呈现群体参数（之前的方式侧重点在原始数据本身），主要是中位数和四分位数。

• 线性系统(Linear System)

  • 标量(scalar)：一个单一的数值
  • 向量(vector)：包含了多个元素的数据
  • 维度(dimension)

• 矩阵

  $$\begin{gathered} \left[\begin{array}{c}11\\ 10\end{array}\right]=\left[\begin{array}{c}53\\ 24\end{array}\right]\left[\begin{array}{c}1\\ 2\end{array}\right] \\ 输出=线性系统\ast 输入 \end{gathered}$$

  把输入向量放横，再和结算系统的每一行元素分别相乘，即获得对应的输出元素。

  

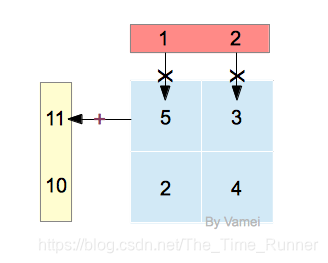
  矩阵 = 线性系统

• 信号(singal)

  我们的社会信息化，是建立在信号的基础上的。

  信号是随着时间或者空间变化的序列。

  在信号处理中，我们常用“信号”来特指一维信号，也就是只随单一一个时间或空间维度变化的序列，这样的信号在数学上可以表示成$f(t)$或者$f(x)$这样一个函数。与一维信号形成对应的是多维信号，比如说图像是二维信号，它随$x,y$两个空间维度变化，从数学上表示成为$f(x,y)$。

  信号处理的方法可以通用于任何一个领域的信号(无论是通信、金融还是其他领域)，这也是信号处理的魅力所在。

• 简谐波(simple harmonic)

  正弦波(sine wave)和余弦波(cosine wave)统称为简谐波。

  正弦波可以写成函数的形式:
  $$y(t)=A\cdot sin(2\pi ft+\varphi )=A\cdot sin(wt+\varphi )$$
  一个简谐波三个参数，振幅(A, amplitude)、频率(f,frequency)、相位(phi, phase).

  简谐波虽然简单，但对信号处理具有重要意义。

• 傅立叶变换 (Fourier Transform)

  傅立叶定理($Fourierinversiontheorem$)：

  任何一个信号都可以由简谐波相加得到

  一个信号由多个频率的简谐波相加得到。组成信号的某个简谐波，称为信号的一个分量(component)。

  傅立叶变换是一套固定的计算方法，用于算出信号的各个分量.

  在信号处理时，可以将信号进行傅立叶变换，转换为简谐波的组合。通过分别控制各个频率上的简谐波分量，我们可以更加有效的进行信号处理。

  比如说，如果信号f(x)是周期性的，我们可以将它变换成：
  $$\frac{a_0}{2}+\sum _{n=1}^{\infty }[a_{n}cos(nx)+b_{n}sin(nx)]$$

  $a,b$代表了信号在各个频率上的简谐波分量的强弱(以及相位),可以通过原信号求得的参数为:
  $$\begin{gathered} a_n=\frac{1}{n}{\int }_{-\pi }^{\pi }f(x)cos(nx)dx,n\ge 0 \\ {b}_n=\frac{1}{n}{\int }_{-\pi }^{\pi }f(x)sin(nx)dx,n\ge 1 \end{gathered}$$

• 频谱(frequency spectrum)

  通过傅立叶变换，我们可以得到一个信号f(t)的不同频率的简谐波分量。

  每个分量的振幅，代表了该分量的强弱。

  将各个频率分量的强弱画出来，可以得到信号的频谱。

  通过信号->Fourier Transform->频谱，我们可以从简谐波分量的角度，理解复杂信号是由哪些简谐机制合成的。

  频谱为我们提供了理解信号的另一个视角。在频率的世界里，我们可以发现很多原信号中一些可能被忽视的信息.

• 图像处理(Image Processing)

  把傅立叶变换用于二维信号，即图像.

  在与原图像混合在一起的噪声，在频谱上则和图像区分开。通过高频滤波技术，就可以过滤掉噪声。这也是图像降噪的一大方法。