Vamei博客学习笔记（2）

本次笔记取材于：

1. 概率论02 概率公理
2. 概率论03 条件概率
3. 概率论04 随机变量

• 概率论的公理化体系

  • 1933年，俄国数学家$AndreiN.Kolmogorov$建立了概率论的公理化体系，严格定义了概率论的语言
  • 概率论的公理化体系同样基于集合论。
  • 这一公理体系的核心是“概率测度”。

• 实验与样本空间

  • 实验：任何一个过程，如果它的结果是随机的(无法事前知道)，那么该过程就称为一个实验
  • 样本空间(sample space)：实验所有可能的结果组成的一个集合(set)，用$\Omega$表示。

  对于概率论来说，集合是“如来佛的手掌心”。

  样本空间包含了概率论研究的基本元素，也就是实验的结果。它们好象化学里的原子。在掷撒子的游戏中，1，2，3，4，5，6，这些结果就构成了我们的原子。实际应用中我们可能对原子构成的分子更感兴趣，在概率论中分子就是样本空间的子集。

  • 事件（event）：样本空间的一个子集，被称为一个事件(event)。

    可以将事件理解为一些特定结果的合集。通过事件，我们可以将结果“聚合”，从而在高一层的单位上进行概率研究。

  • 补集：事件A的补集包含所有不属于A的样本空间元素。

  • 交集：包含了所有既在A中又在B中的元素。

  • 并集：包含了所有在A中或者在B中的元素

  • 空集$\Phi$：是一个不包含任何元素的集合。

• 交并集运算法则

• 概率测度

  概率测度是基于样本空间$\Omega$的一个函数$P$。这个函数$P$定义了从样本空间的子集(即事件)到实数的映射，且满足下面的条件:

  1. $P(\Omega )=1$ (概率的特征)
  2. 如果$A\subset \Omega$, 那么$P(A)\ge 0$ (概率的特征)
  3. 如果$A_1$和$A_2$不相交，那么 $P(A_1\cup A_2)=P(A_1)+P(A_2)$ （测度的特征）

  “测度”这个词是在提示我们概率定义的基础是“测度论”。

  “测度”是集合的子集到实数的一个映射。

  比如一个正方形的面积为6，实际上是说，一个点的集合（正方形）的某个“测度”为6，即点的集合和实数6对应。“面积”的一个关键特点是可加。

通过概率论的公理体系，侧面定义了概率，但并没有直接对概率是什么清晰表述。对概率的本质有两种观点：频率观点和贝叶斯观点。

1. 在频率观点中，如果我们以相同的条件重复尝试N次，那么如果某个事件出现了n次，那么该事件的概率为P(A)=n/NP(A)=n/N。（大数定律）
2. 在贝叶斯观点中，概率代表了主观上对某一论断的信心。

• 测度论（维基百科）

  数学上，测度（英语：measure）是一个函数，它对一个给定集合的某些子集指定一个数，这个数可以比作大小、体积、概率等等。

  传统的积分是在区间上进行的，后来人们希望把积分推广到任意的集合上，就发展出测度的概念，它在数学分析和概率论有重要的地位。

  测度论是实分析的一个分支，研究对象有σ代数、测度、可测函数和积分，其重要性在概率论和统计学中都有所体现。

• 条件概率

  为了深入探索概率中包含的数学结构，数学家进一步构筑了“条件概率”。

  为了表达某一事件(治疗)对另一个事件(康复)概率的影响，概率论中引入条件概率的概念。

  如果A和B是两个事件，且P(B)≠0。那么B条件下，A的条件概率为
  $$P(A|B)=\frac{P(A\cap B)}{P(B)}$$
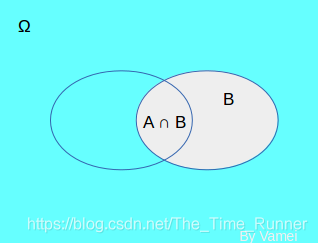
  当确定B发生时，样本空间不再是$\Omega$，而是缩小成B.我们在B样本空间中寻找A发生的概率。从下面的图中看，就是$A\cap B$的面积(概率测度)，除以B占据的面积(概率测度)，也就是我们条件概率的定义。

• 条件概率推论（1）

  A和B为两个事件，且$P(B)̸=0$。那么:
  $$P(A\cap B)=P(A|B)P(B)$$
  允许我们从条件概率，来推导两个事件同时发生的概率。

• 条件概率推论（2）

  有事件$B1,B2,...,Bn$。如果${\bigcap }_{i=1}^n{B}_i=\Omega$，两个不同事件互斥$(Bi\cap Bj=\Phi$, 如果$i̸=j$），且任意$P(B_i)>0$。那么，对于任意事件$A$：
  $$P(A)=\sum _{i=1}^{n}P(A|B_i)P(B_i)$$
  这个推论的要点是:

  1. 不同的$B$事件互斥(不相交)

  2. 所有$B$事件的并集是$\Omega$。

  3. 每个元素都必须且只能进入一个$B_i$。

     在这样的条件下，我们说$B_1,B_2,...,B_n$是样本空间的一个分割(partion)。

• 独立事件

  两个事件可以是相互独立(independent)的。直观的讲，如果事件A发生与否不会影响事件B的概率，那么A与B独立。

  两个事件$A$和$B$，$P(A)!=0$，$P(B)!=0$。如果$P(A|B)=P(A)$，或者$P(B|A)=P(B)$，那么事件$A$和$B$是独立事件。

  根据独立事件和条件概率的定义可以推知，如果
  $$P(A\cap B)=P(A)P(B)$$
  那么A和B独本

• 贝叶斯法则

  如果$A$和$B1,B2,...,Bn$为事件，$B_i$互斥，${\bigcap }_{i=1}^n{B}_i=\Omega$， 且$P(B_i)>0$。那么
  $$P(B_j|A)=\frac{P(A|Bj)P(Bj)}{{\sum }_{i=1}^{n}P(A|B_i)P(B_i)}$$

  这个法则是一种求条件概率的方式。 贝叶斯法则常用于求一些比较难以直接获得的条件概率。此外，在机器学习中，也有贝叶斯算法的应用。

• 随机变量(random variable)

  随机变量(random variable)的本质是一个函数，是从样本空间的子集到实数的映射，将事件转换成一个数值。我们通常用一个大写字母来表示一个随机变量，比如$X$。

  根据样本空间中的元素不同(即不同的实验结果)，随机变量的值也将随机产生。

  可以说，随机变量是“数值化”的实验结果。

  在现实生活中，实验结果可以是很“叙述性”，比如“男孩”，“女孩”。在数学家眼里，这些文字化的叙述太过繁琐，我们为什么不能拿数字来代表它们呢？

• 离散随机变量

  在连续掷两次硬币的例子中，样本空间为:
  Ω = { H H , H T , T H , T T } Ω=\{HH,HT,TH,TT\} Ω={HH,HT,TH,TT}
  这样的实验结果可以有很多数值化的方法，比如定义HH为400， HT为30， TH为0.2，TT为1。(数值化方式是人为定义的，具体应该怎么定义是根据现实需求来的)。

  比如说，根据出现正面的次数，我们将赢取不同的奖励。那么在分析时，可以取“结果中正面的次数”为随机变量。这样一个随机变量将有2, 1, 0三种可能的取值。

  该随机变量只能取离散的几个孤立值，这样一种随机变量称为离散随机变量。

  映射关系如下:

  实验结果	随机变量
  HH	2
  HT	1
  TH	1
  TT	0

  如果样本空间中的每个结果等概率，那么随机变量取值可能性为:
  $$\begin{gathered} P(X=2)=0.25 \\ P(X=1)=0.5 \\ P(X=0)=0.25 \end{gathered}$$

  当$X$取$0,1,2$之外的值时，概率为$0$；所有可能取值的概率和为1。

  $X=1$这个事件，实际上包含了两个元素：$HT,TH$。因此，$X=1$出现的概率较高。

• 随机变量的概率公式

  • 离散单个取值：概率质量函数(PMF, probability mass function)

    $P(X=x)$表示了随机变量在不同取值下的概率，称为概率质量函数(PMF, probability mass function)。

  • 离散累计取值：累积分布函数(CDF, cumulative distribution function)

    累积分布函数(CDF, cumulative distribution function)来表示随机变量的概率分布状况。在累积分布函数，我们列出的，总是随机变量X，在小于x的这个区间的概率和。

    当x增大时，X < x包含的结果增加，概率和也相应增加。当x为正无穷时，实际上是所有情况的概率和，那么累积分布函数为1。
    $$F(x)=P(X\le x),-\infty <x<\infty$$
    累计分布函数的优势在于，它可以同时用于离散随机变量和连续随机变量。

  • 连续局部取值：概率密度函数(PDF，probability density function)

    概率密度函数，并不能对应离散随机变量单个取值下的概率。虽然称为概率密度函数，但并非概率。

    离散随机变量，由单个的概率质量函数到汇总的累计分布函数，是加法；平行维度

    连续随机变量，由汇总的累计分布函数到局部的概率密度函数，是求导；降低了一个维度。

    我们在某个点附近取一个“无穷小”段，该小段的区间长度为dx，而这个“无穷小”段对应的概率为dF，那么该点的概率密度为dF/dx。

    概率密度函数可以代替累积分布函数，来表示一个连续随机变量的概率分布:
    $$f(x)=dF(x)dx$$
    即密度函数是累积分布函数的微分，或者说，
    $$F(x)={\int }_{-\infty }^{x}f(u)du$$
    即累积分布函数是密度函数从负无穷到x的积分。

    密度函数满足:
    $${\int }_{-\infty }^{+\infty }f(u)du=1$$

• 连续随机变量(continuous random variable)

  比如，一个随机变量，可以随机的取0到1的任意数值。当这样取值时，任意区间能实际上都有无穷多个结果。

  每个结果的可能性都是无穷小。我们讨论的是某个区间内的概率，即$P(a<X<b)$，而不是具体某一数值的概率。显然，我们无法用概率质量函数来描述连续随机变量的分布。

  对于连续随机变量，我们只讨论某个区间，比如从1.2到1.4这一区间的概率，而不讨论具体某个点，比如1.3的概率。累积分布函数本身就表示随机变量在一个区间概率，所以可以直接用于连续随机变量。

• 均匀分布

  假设我们有一个随机数生成器，产生一个从0到1的实数，每个实数出现的概率相等。这样的一个分布被称为均匀分布(uniform distribution)。

  它的累积分布函数是:
  $$\begin{gathered} F(x)=0,x<0 \\ F(x)=x,0\le x\le 1 \\ F(x)=1,x>1 \end{gathered}$$
  他的概率密度函数可以写成:
  $$f(x)=\{\begin{array}{l}1,0\le x\le 1\\ 0,x,0orx>1\end{array}$$