第十四届蓝桥杯_Java_A组_与或异或

最新推荐文章于 2025-03-07 09:38:35 发布

原创最新推荐文章于 2025-03-07 09:38:35 发布 · 681 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯 #java #算法

Java 专栏收录该内容

4 篇文章

订阅专栏

本文展示了两个Java代码示例，一个是使用`BinaryOperator`实现AND、OR和XOR操作的组合计数，另一个是深度优先搜索算法在电路分析中的应用。通过递归计算有效组合数和电路中满足特定条件的路径数。

问题描述

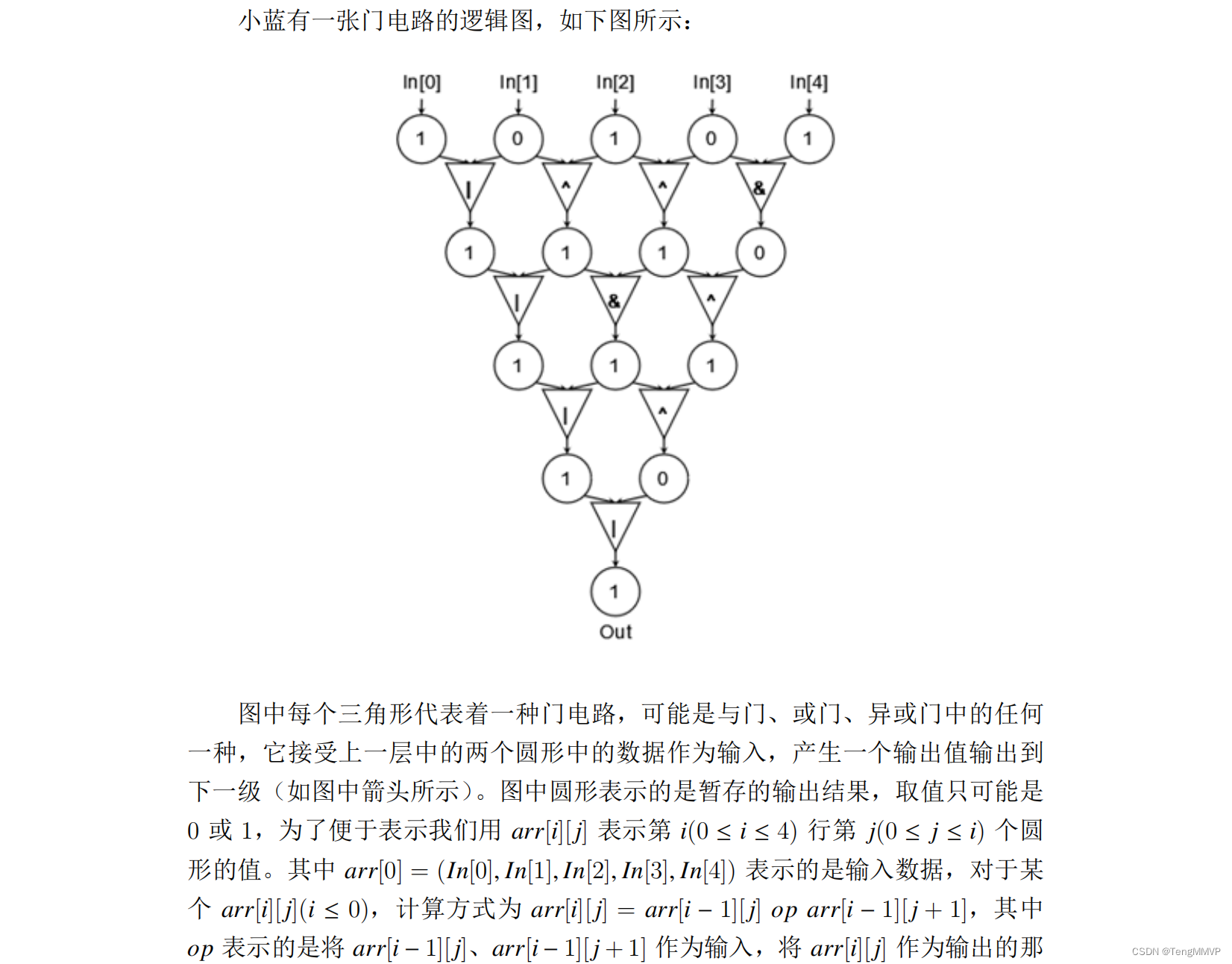
参考代码

示例一

import java.util.function.BinaryOperator;

public class Main {
    // AND、OR和XOR操作的二元操作符
    private static final BinaryOperator<Integer> AND = (x, y) -> x & y;
    private static final BinaryOperator<Integer> OR = (x, y) -> x | y;
    private static final BinaryOperator<Integer> XOR = (x, y) -> x ^ y;
    private static final BinaryOperator<Integer>[] operations = new BinaryOperator[]{AND, OR, XOR};

    // 计算有效组合数的方法
    public static int countValidCombinations(int level, int[] values) {
        // 基本情况：如果我们已经到达最后一级
        if (level == 1) {
            return values[0] == 1 ? 1 : 0;
        }

        int validCombinations = 0;
        // 生成当前级别的所有可能组合
        for (int opIndex = 0; opIndex < Math.pow(3, level - 1); opIndex++) {
            int[] newValues = new int[level - 1];
            int tempIndex = opIndex;

            // 计算当前组合的输出
            for (int i = 0; i < level - 1; i++) {
                int op = tempIndex % 3;
                tempIndex /= 3;
                newValues[i] = operations[op].apply(values[i], values[i + 1]);
            }

            // 递归计算下一级别的组合数
            validCombinations += countValidCombinations(level - 1, newValues);
        }
        return validCombinations;
    }

    public static void main(String[] args) {
        // 初始输入值
        int[] inputValues = {1, 0, 1, 0, 1};
        // 从顶级开始计数
        int result = countValidCombinations(inputValues.length, inputValues);
        // 输出结果
        System.out.println("总的有效组合数：" + result);
    }
}

示例二

public class Main {
    private int[][] circuit = new int[6][6];
    private int answer = 0;
    private final int target = 1;

    public static void main(String[] args) {
        new Main().run();
    }

    private void run() {
        // 初始化电路的基本情况。
        circuit[5] = new int[]{0, 1, 0, 1, 0, 1};
        // 从电路的顶部开始深度优先搜索。
        depthFirstSearch(1, 5);
        // 打印计算出的答案。
        System.out.println(answer);
    }

    private void depthFirstSearch(int index, int level) {
        if (level <= 1) {
            // 基本情况：如果当前单元格与目标匹配，增加答案。
            if (circuit[level][index] == target) {
                answer++;
            }
        } else {
            if (index < level) {
                // 执行与运算并继续搜索。
                circuit[level - 1][index] = circuit[level][index] & circuit[level][index + 1];
                depthFirstSearch(index + 1, level);
                // 执行或运算并继续搜索。
                circuit[level - 1][index] = circuit[level][index] | circuit[level][index + 1];
                depthFirstSearch(index + 1, level);
                // 执行异或运算并继续搜索。
                circuit[level - 1][index] = circuit[level][index] ^ circuit[level][index + 1];
                depthFirstSearch(index + 1, level);
            } else {
                // 移动到电路的下一个深度级别。
                depthFirstSearch(1, level - 1);
            }
        }
    }
}