logistic regression 求解过程

arameter Optimization in Logistic Regression

1. Objective Function: Logistic regression aims to optimize the log-likelihood function (or equivalently minimize the negative log-likelihood) based on the observed data. For a binary classification problem, the log-likelihood is given by:

   

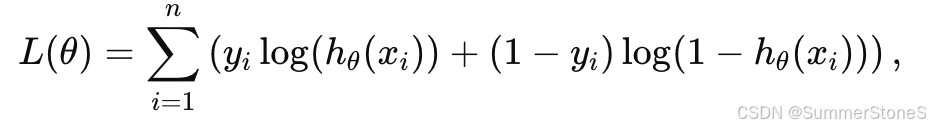
   where:

   • yi is the observed label (0 or 1).
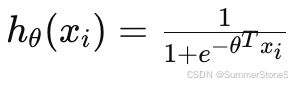   • ​ is the sigmoid function representing the predicted probability.
   • θ represents the parameters to be optimized.

2. Convexity of the Objective:

   • The sigmoid function hθ(xi) is convex in its input.
   • The negative log-likelihood −L(θ) when expressed as a function of θ, is a convex function because it is the composition of a convex function (logistic loss) with a linear function.
   • This convexity ensures that any local minimum of the objective is also a global minimum.

3. Optimization Method:

   • Logistic regression typically uses gradient-based optimization algorithms to find the optimal parameters θ. Common methods include:
     • Gradient Descent: Iteratively updates θ in the direction of the negative gradient of the loss function.
     • Newton's Method: Uses the second derivative (Hessian) of the loss function for faster convergence.
     • Stochastic Gradient Descent (SGD): Processes data in mini-batches for scalability with large datasets.

4. Convergence:

   • Since the problem is convex, gradient-based methods are guaranteed to converge to the global optimum, provided the learning rate or step size is appropriately chosen.