数据科学家基础知识篇（面试小朋友）-优快云博客

本文链接：https://blog.youkuaiyun.com/SummerStoneS/article/details/144812384

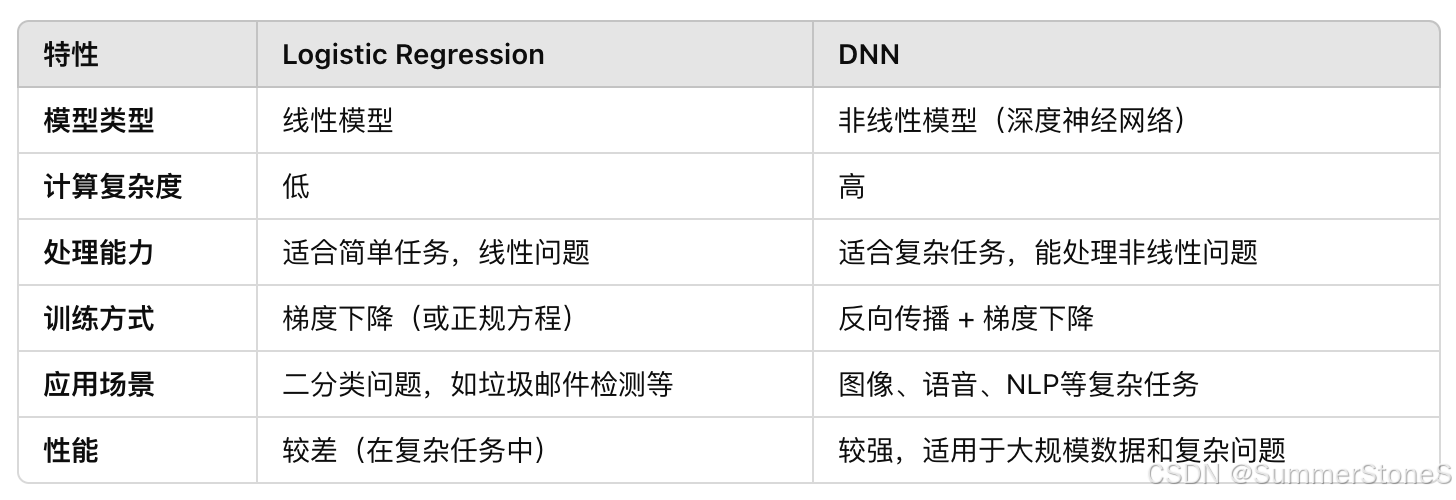
1. 如何选择模型？（模型的评估标准）

选择泛化误差generalization error最小的
考虑数据量，特征的类型，特征跟y是否是线性关系，问题是分类还是回归
在这里插入图片描述
2. 什么是误差？以及泛化误差？
误差：学习器的预测值与实际输出的差异

泛化误差：学习器在新样本上的误差

训练误差/经验误差：学习器在训练集上的误差

3.过拟合、欠拟合

过拟合：训练误差小，而泛化误差大，模型过度学习了训练样本的特征，有些特征不具有一般性
欠拟合：训练误差大，模型对训练样本的一般性质尚未学好

如何解决过拟合：
– 正则
– dropout
– 提前结束训练，当validation dataset的准确性下降的时候

如何解决欠拟合：
– 决策树学习中扩展分支
– 增加迭代次数

5. 怎么选L1正则还是L2

L1（lasso)这么好用为什么不用岭回归还考虑最普通的线性回归或者L2
– L1用在特征选择，但不是无偏估计；
– 如果是为了预测准确，以及beta的解释性，用L2更好；
为什么神经网络用L2正则不用L1
– 梯度不连续，影响收敛
– 造成权重的稀疏性，用dropout更合适，更关注权重跟权重之间的关联，没用的权重让它变小就好了

Elastic Net: 兼顾L1正则和L2正则，对于高维数据，变量高度相关和多重共线性强的情况下，避免L1(Lasso)直接去掉某些特征
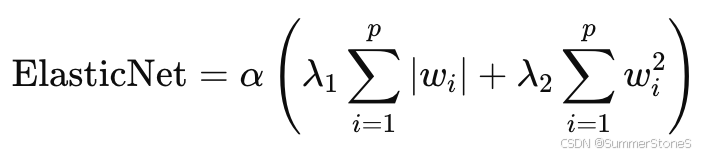
在这里插入图片描述

6.偏差，方差，噪声
模型的泛化误差可以分解为偏差、方差与噪声之和
$bias^2 (x) + var(x) + \epsilon^2$
偏差：模型期望预测与真实标记的差，刻画算法本身的拟合程度
方差：数据扰动导致的学习性能的变化，不同的数据进入模型预测产生的预测结果的波动
$E[(f(x;D) - 模型期望输出(x)])^2]$
bias-variance dilemma
在训练不足时，模型拟合能力不够强，训练数据的扰动不足以使模型产生显著的变化，这时偏差大，方差小，偏差主导泛化错误率；随着训练程度的加深，模型拟合能力逐渐增强，训练数据发生的扰动能渐渐被模型学习到，方差逐渐主导了泛化错误率；在训练程度完全充足后，训练数据发生的轻微扰动都能使模型发生显著变化，训练数据自身的非一般性的特质被学习到，发生过拟合

7. 交叉验证是什么
One common approach to cross-validation is k-fold cross-validation, where the data is divided into k equally-sized folds. The model is trained on k-1 folds and tested on the remaining fold. This process is repeated k times, each time using a different fold as the test set. The performance metrics from each iteration are then averaged to provide an overall estimate of the model’s performance.
assess model performance, prevent over-fitting, hyper parameter tuning, model selection
8. 建模前的流程

缺失值处理、数据检查
标准化
– 为什么要做标准化（加速收敛，使梯度在各个方向上差不多；避免不同feature有不一样的量纲，模型会偏向量纲更大的feature，并且权重不好解释，）
– 先做标准化还是先分训练集测试集？答案是先分训练集测试集；
正确的做法是用训练数据算出mean,std(min,max)，然后用该值去归一化test数据
Do not use minmax_scale unless you know what you are doing. A common mistake is to apply it to the entire data before splitting into training and test sets. This will bias the model evaluation because information would have leaked from the test set to the training set. In general, we recommend using MinMaxScaler within a Pipeline in order to prevent most risks of data leaking: pipe = make_pipeline(MinMaxScaler(), LogisticRegression()).

离群值检测Outlier detection

为什么要做离群值检测
– 影响模型的拟合，造成模型偏差较大；线性回归里离群值的误差占总的误差会比较大，影响系数的估计
– 影响鲁棒性离群值会让树模型增加不必要的分支，降低模型的泛化性能；（让模型对噪声更加鲁邦，不要对异常值过度拟合）
– 避免噪声对模型误导，有些离群值是由输入错误，设备故障导致的，这些数据不能被当做正常数据处理
– 影响收敛速度，梯度下降中，离群值会造成较大的梯度，延缓收敛速度
如何进行离群值检测
机器学习法
–isolation forest https://zhuanlan.zhihu.com/p/38138946
– oneclassSVM
– DBSCAN
统计方法：
– 箱图低于1/4分位点-1.5倍IQR（四分位距）或高于 3/4分位点+1.5倍IQR
– 正态分布大于3倍标准差
– 专家经验
测试集和训练集的划分
尽可能保持数据分布一致，both dependent variables and independent variables

极大似然法的核心思想：令每个样本属于其真实标记的概率越大越好；每个样本在已知参数下 (以logistic regression为例）

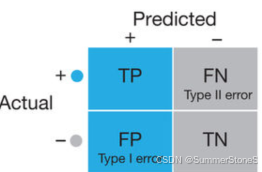
一类错误二类错误以及和假设检验的关系
一类错误：本来没病，说他有病/原假设是对的，拒绝了原假设（如果太高，在营销场景里会导致花费过大）
二类错误：本来有病，说他没病（如果太高了，在医疗场景里会导致更多死亡）

原假设是没有差别（没病）（通常跟我们关心的要证明的是反的）

比较均衡的评估分类效果的F1-score
$\frac{2}{\frac{1}{recall} + \frac{1}{precision} } \\ recall = \frac{tp}{fp+tp} \\precision=\frac{tp}{tp+fn}$

p值：拒绝原假设的最小的alpha(1-置信区间）；拒绝原假设意味着显著
p值很小说明拒绝原假设（即两者的均值不想等，但不代表接受了两者的差异值就是这个影响）

9.线性回归基本假设

y和x线性相关
零条件均值：残差的期望是0，残差和x不相关，给定任何x值，残差的期望都是0 E[ u | x ] = E[ u ] = 0
样本有变化，x的方差不能是0，beta = cov(x, y) / var(x)
随机抽样
同方差性
前4个假设保证系数的无偏性，第四个假设是为了得到OLS估计量的方差
$βj^～N(βj,σ2Sxx)Sxx是x的方差 \hat{\beta_j} ～ N(\beta_j, \frac{\sigma^2}{S_{xx}}) \\ S_{xx}是x的方差$
多元线性回归假设加了一个：
6.不完全共线性（完全共线性：某个x可以被其他的x完全线性表示）Perfect multicollinearity: One x can be perfectly linearly represented by other x’s.
共线性的存在不影响OLS（系数）的无偏估计, 影响的是系数的方差
$var(βj^)=σ2SSTj(1−Rj2)SSTj:xj的方差，xj的样本方差越大（波动大或者样本总量达），系数的估计的方差越小Rj2是xj总波动中可以被其他x解释的部分，当xj可以完全由其他自变量解释时，var(βj^)会趋向于无穷大VIFj=11−Rj2又称为方差膨胀因子 var(\hat {\beta_{j}}) = \frac{\sigma^2}{SST_j(1-R_j^2)} \\ SST_j: x_j的方差，x_j的样本方差越大（波动大或者样本总量达），系数的估计的方差越小 \\ R_j^2是x_j总波动中可以被其他x解释的部分，当x_j可以完全由其他自变量解释时，var(\hat{\beta_j})会趋向于无穷大 \\ VIF_j = \frac{1}{1-R_j^2} 又称为方差膨胀因子$
VIFj 大于10，说明Xj可以被其他自变量解释90%，如果我们很关心Xj对y的影响的时候，那我们需要去关心xj跟其他自变量的共线性问题；如果我们关心的是另一个x1对y的影响，那么Xj和其他自变量的共线性完全不会影响x1系数的估计的方差

R方：y的样本波动可以被线性回归解释的部分
$R^2 = SSE / SST$
SSE : 样本预测值 y-hat 对 y均值的方差
SST：样本y实际值相对y均值的方差（波动）

10. OLS参数估计

矩估计（矩是用来描述随机变量分布的，一阶平均值，二阶方差，三阶偏度）
主要用到的是1. E(u) = 0, 2. E(xu) = 0, 核心是把u替换成
$u=y−βix−β0从而有E(x(y−βix−β0))=0E(y−βix−β0)=0进一步用样本平均值代替E(x)1n∑(yi−β0^−β1^xi)=01n∑(yi−β0^−β1^xi)xi=0 u = y - \beta_ix-\beta_0 \\从而有 \\ E(x(y - \beta_ix-\beta_0))=0 \\ E( y - \beta_ix-\beta_0) = 0 \\进一步用样本平均值代替E(x) \\ \frac{1}{n} \sum(y_i - \hat{\beta_0}-\hat{\beta_1}x_i) = 0 \\ \frac{1}{n} \sum(y_i - \hat{\beta_0}-\hat{\beta_1}x_i) x_i= 0$
2.MSE 最小二乘估计
写出MSE的表达式
$\sum [y_i-(\beta_0 + \beta_1x_i)]^2$
然后MSE表达式对beta0, beta1分别求导=0
AUC通俗解释

一个正样本和一个负样本，正样本分数比负样本分数高的概率，瞎猜是0.5，所以基线是0.5
横轴是false positive rate, 纵轴是true positive rate(recall)
model’s ability to distinguish positive samples and negative samples
$\frac{fp}{tn + fp(下面一行)} \\ true ~positive~ rate(recall) = \frac{tp}{tp + fn(第一行)}$
precision = tp/predicted positive预测是正的
why not use accuracy?
when the samples are not balanced,负样本很多，正样本很少，模型倾向于都预测称负的，accuracy也很高

Batch normalization 和layer normalization
batch normalization: 同一个batch的样本在不同特征上分别做normalization
layer normalization: 同一个样本在不同特征上做normalization，多用于文本，比如一个字有512维，这512维做一次normalization
NLP任务中，不同样本的序列长度不一样，没法在不同样本的同一特征上做序列标准化

目的都是解决训练过程中可能出现的梯度消失和梯度爆炸的问题，达到更快收敛的目的
https://zhuanlan.zhihu.com/p/647813604

RNN、LSTM
RNN不是很能处理序列的长距离依赖
LSTM加入了遗忘门（决定哪些信息遗忘），输出门，输入门（决定哪些信息保留）相比RNN更好地考虑了长距离问题，但是
跟transformer相比，这两者都是序列输入的，（不利于并行，梯度消失会造成长距离依赖都是问题）

transformer为什么用multi-head attention
通过关注输入中的不同部分，学习序列中的多样关系
单一的注意力头可能只能专注于一种关系（例如，一个词与下一个词的关系）
Multi-Head Attention 通过多个注意力头并行工作，每个头有独立的参数，可以学习和关注输入数据中的不同关系和特征。例如：
一个头可能关注语法关系（如主谓结构）。
另一个头可能关注长距离的上下文依赖。

Catboost
CatBoost和XGBoost、LightGBM并称为GBDT的三大主流神器，都是在GBDT算法框架下的一种改进实现
LightGBM有效的提升了GBDT的计算效率，而Yandex的CatBoost号称是比XGBoost和LightGBM在算法准确率等方面表现更为优秀的算法
catboost:对类别进行了很好的处理，一般算法就是对类别特征进行one-hot，或用类别里的标签平均值进行替代，catboost会计算类别的期望标签
catboost会考虑特征组合，不光是类别型特征的相互组合，对于数值型的变量也会在分割的时候把切割的左右各自当成一种特征然后考虑跟其他特征的组合
CatBoost使用对称树（oblivious trees）作为基预测器。在这类树中，相同的分割准则在树的整个一层上使用。这种树是平衡的，不太容易过拟合。特征分割的时候也利用了直方图，（将特征离散化到固定数量的箱子中以减少内存使用），跟lightGBM一样高效
解决梯度偏移的问题（没看懂）

t检验，AB-test
t检验的条件：
完全随机分组
服从正态分布，两组方差一致（方差齐性检验，服从F分布）
在这里插入图片描述

要得到观测到的两组区别（MDE）（销量上的差异、单店毛利的差异），在显著性水平为10%（alpha）,统计效力为80%的情况下，样本要达到多少；

propensity score
解决的是AB组没法随机分的问题
通过对所有可以分的个体做预测，例如logistic regression，预测每个个体的倾向性得分，得分差不多的人分成A和B，让A和B比较相似比较balance

支持向量机的loss function
$\ \frac{1}{2}||w||^2 \\ s.t. \ y_i(w_{}^{T}x_i + b) \geq 1 ~~~~~~~~for ~~i = 1,2,..., m$
wx + b = 0是分割的超平面的表达式

神经网络篇

各种激活函数比较
https://blog.youkuaiyun.com/weixin_44115575/article/details/139835864
softmax将logits(神经元的输出映射为概率，多分类
sigmoid 可以将输出映射为0-1之间的
在这里插入图片描述
如何预防梯度消失和梯度爆炸
– 选择合适的激活函数：使用ReLU或其变种（如Leaky ReLU、ELU等），可以有效防止梯度消失，并且在一定程度上减少梯度爆炸的可能性。
– 适当的权重初始化：使用Xavier或He初始化等方法，可以避免权重值过大或过小，从而减少梯度消失和梯度爆炸的风险。
– 梯度裁剪：当发生梯度爆炸时，采用梯度裁剪可以限制梯度的范围，避免参数更新过大，保证训练过程的稳定性。
– 使用Batch Normalization：Batch Normalization通过标准化每一层的输入，减小了梯度消失和爆炸的风险，稳定了训练过程。

logistic regression怎么做多分类

One-vs-Rest (OvR) or One-vs-All (OvA)
In this approach, you train a separate binary logistic regression classifier for each class. Each classifier is trained to distinguish one class from all the others. During prediction, each classifier produces a probability score for its respective class. The class with the highest probability is chosen as the final prediction.
Softmax Regression (Multinomial Logistic Regression)
This approach extends logistic regression to multiple classes by using the softmax function, which is a generalization of the logistic function to multiple classes.

The softmax function for class k is defined as:
$\frac{e^{\theta_k^T x}}{\sum_{j=1}^{K} e^{\theta_j^T x}}$
theta_k is the parameter vector for class k
The model is trained by optimizing the cross-entropy loss function, which measures the performance of the classification.

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# One-vs-Rest approach
model_ovr = LogisticRegression(multi_class='ovr', max_iter=200)
model_ovr.fit(X_train, y_train)
y_pred_ovr = model_ovr.predict(X_test)
print("One-vs-Rest Accuracy:", accuracy_score(y_test, y_pred_ovr))
# Softmax Regression approach
model_softmax = LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=200)
model_softmax.fit(X_train, y_train)
y_pred_softmax = model_softmax.predict(X_test)
print("Softmax Regression Accuracy:", accuracy_score(y_test, y_pred_softmax))

dropout在训练和测试的时候怎么用
– 训练阶段：Dropout层启用，dropout层以概率p随机丢弃神经元。
– 预测阶段：Dropout层禁用，所有神经元参与计算，输出根据丢弃概率进行缩放。乘(1-p)

model = Sequential([
    Dense(128, activation='relu', input_shape=(input_dim,)),
    Dropout(0.5),
    Dense(64, activation='relu'),
    Dropout(0.5),
    Dense(num_classes, activation='softmax')
])

logistics regression参数求解过程
极大似然，每个点都以最大的概率按照其真实值出现，概率相乘；
对数似然函数
梯度下降法（或牛顿法）求解；是凸问题

TF-IDF

用于信息提取
TF: 词在这个文档中的频率
IDF：
$\frac{1}{log(\frac{文档总数}{包含该词的文档数+1})} = \frac{1}{log(\frac{1}{包含该词的文档数占比})}$
一个词在这个文档中出镜率高，在其他文档中出镜率低，就更容易成文这个文档的关键信息
缺点是没有考虑上下文关系和词的位置，只考虑了词频，一般不如词向量模型的embeddings
优点是好计算