智能密度每季度翻倍,边缘AI爆发进入倒计时。
清华大学和面壁智能团队,在《自然-机器智能》(Nature Machine Intelligence)上的一项研究通过详尽的数据分析揭示了大语言模型进化的隐藏规律:致密律(Densing Law)。


研究指出为了获得同等水平的智能,模型所需的参数量正在呈指数级下降。
从暴力堆砌到智能致密
在人工智能的发展历程中,很长一段时间里行业信奉单一的信条,那就是缩放定律(Scaling Law)。
这个定律告诉我们模型越大性能就越强。
为了追求极致的智能表现,GPT-3 将参数量推到了 1750 亿,PaLM 更是达到了惊人的 5400 亿。
堆砌参数在初期确实带来了显著的效果,但也迅速撞上了现实的墙壁。
推理成本超过了训练成本,庞大的模型体积难以塞进手机等边缘设备,高昂的算力消耗让应用落地变得极其昂贵。
物理学用质量除以体积来定义密度,研究人员引入了类似的概念,将能力密度(Capability Density)定义为单位参数量内所包含的智能水平。
这一指标直接反映了模型利用参数存储和处理知识的效率。
研究团队对 Llama-1 发布以来的 51 个主流开源基础模型进行了全方位的分析,这些模型涵盖了 Llama 系列、Mistral、Gemma 等行业标杆。
分析结果揭示了一个清晰的规律:开源大模型的最大能力密度随时间呈现出标准的指数增长。
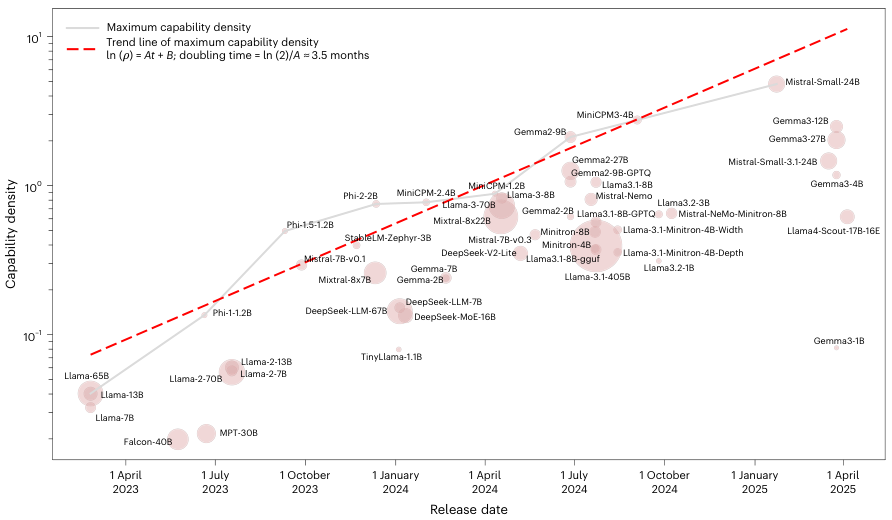
数据清晰地记录了这场剧烈的代际更迭。2023 年 2 月 Llama-1 发布时,其密度值还低于 0.1。
到了近期,Gemma-2-9B 和 MiniCPM-3-4B 等模型的密度值已经接近 2。
这种增长并非线性,而是呈现出惊人的加速度。
通过对 MMLU、BBH、MATH 等五个权威基准测试数据的拟合计算,模型密度的增长系数约为 0.007。
换算成时间周期,这意味着大型语言模型的最大能力密度大约每 3.5 个月就会翻一番。这个速度远超传统硬件领域的摩尔定律。
为了验证这一规律的真实性,排除模型针对测试集刷题的嫌疑,研究人员在专门构建的无污染数据集 MMLU-CF 上进行了二次验证。
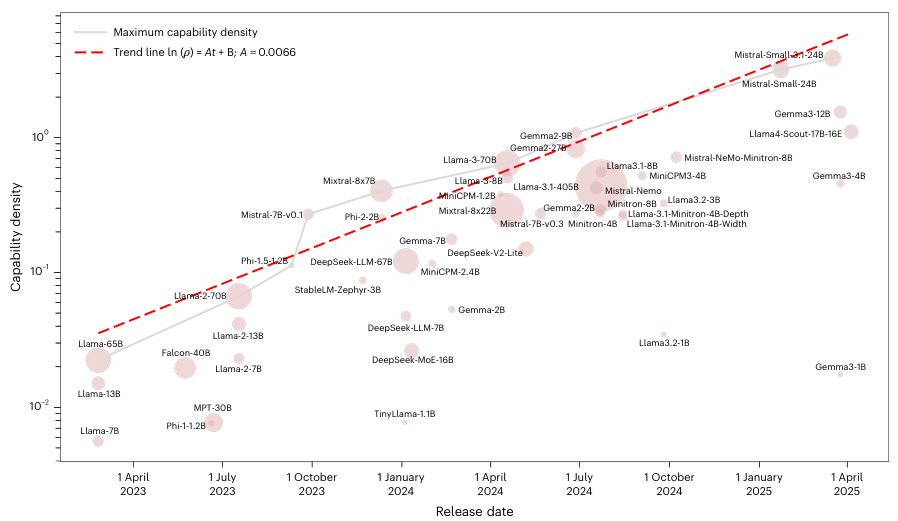
结果显示,即便在完全未见过的数据上,模型能力密度的指数增长趋势依然成立,相关系数高达 0.953。
这证实了致密律反映的是算法效率的真实进步,而非过拟合带来的虚假繁荣。
致密律的发现为评估模型价值提供了全新的视角。
它推导出了一系列反直觉但对产业影响深远的结论,其中最核心的是参数量的半衰期概念。
在保持模型性能不变的前提下,所需的参数量每 3.5 个月就会减少一半。
这一推论在实际产品中得到了验证。
2024 年 2 月发布的 MiniCPM-1-2.4B,其性能已经可以匹敌甚至超越 2023 年 9 月发布的 Mistral-7B。
仅仅过了 4 个月,行业就用 35% 的参数量实现了同等甚至更优的性能。
大模型的发展本质上是在追求更高的效费比,而非单纯的体积扩张。
参数量的减少直接带动了推理成本的下降。
结合 FlashAttention 等显存优化技术的进步,推理成本的下降速度甚至超过了密度的增长速度。
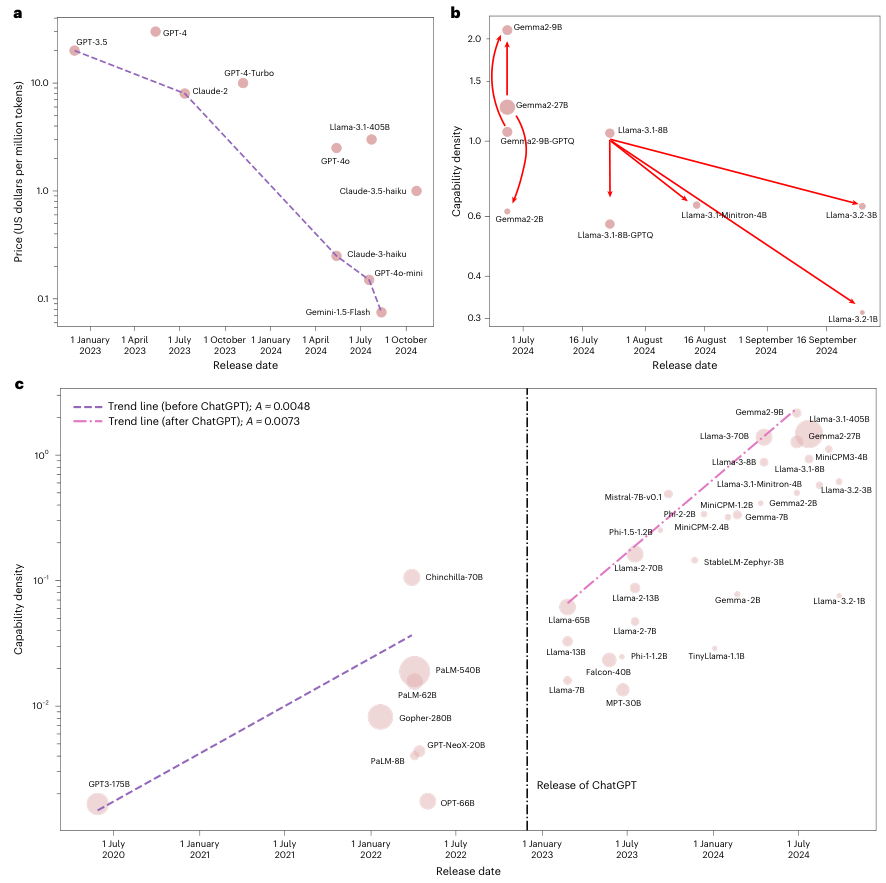
数据显示,推理成本大约每 2.6 个月就会减半。
这种成本结构的改变直接引发了云服务市场的价格战。
2022 年 12 月,GPT-3.5 每百万 token 的价格为 20 美元。
到了 2024 年 8 月,Gemini-1.5-Flash 的同等用量仅需 0.075 美元。
在不到两年的时间里,价格下降了 266.7 倍。这种剧烈的价格变动背后,正是致密律在发挥作用。
压缩与边缘智能
在追求模型轻量化的过程中,开发者习惯使用剪枝(Pruning)、蒸馏(Distillation)和量化(Quantization)等技术来压缩模型。
直觉认为切掉不重要的神经元或降低精度能提高模型的信噪比,从而提升密度。研究结果却给出了相反的结论:盲目压缩往往会降低能力密度。
Llama-3.2-3B 是从 Llama-3.1-8B 剪枝蒸馏而来的版本,但分析显示其密度反而低于原版。
同样,使用 GPTQ 方法量化后的模型,密度通常也会受损。
主要原因在于压缩后的模型往往面临训练不足的问题,小模型没有足够的时间和数据量来彻底吃透知识。
Gemma-2-9B 是一个罕见的成功案例,它由 Gemma-2-27B 蒸馏而来,且展现出了比原版更高的密度。
这表明要想真正提高密度,不能只靠简单的做减法,必须保证压缩后的模型经过充分的再训练。
只有当小模型真正消化了知识,密度才会提升。
致密律描述的是算法层面的优化,即每 3.5 个月智能密度翻倍。
摩尔定律描述的是硬件算力的进步,即芯片性能每 2.1 年翻倍。
当这两股指数级增长的力量汇合时,产生了巨大的乘数效应。
根据测算,在固定芯片价格下,能够运行的最大有效参数规模,也就是等效智能水平,大约每 88 天就会翻倍。
这一增长速度预示着边缘智能(Edge-side Intelligence)的爆发时刻比预期来得更快。
高性能的大模型将迅速跑进智能手机、个人电脑等消费级设备中,无需依赖昂贵的云端集群。
用户将在本地设备上体验到原本只有巨型服务器才能提供的智能服务,这将彻底改变 AI 应用的形态和隐私安全格局。
客观量化智能的科学方法
衡量智能本身是一个极其复杂的难题。
为了保证结论的科学性,研究团队设计了一套严谨的相对密度计算方法,避开了直接定义智能的主观性。
研究首先建立了一个参考系,通过训练一系列不同规模的基准模型,拟合出参数量与损失(Loss)的缩放定律曲线。
随后,将抽象的损失值进一步映射为具体的下游任务分数,建立了损失-分数的关联。
在此基础上,对于任何一个待测模型,根据其在任务上的得分,反推一个标准参考模型达到该得分所需的参数量。
这个反推出来的参数量被称为有效参数规模(Effective Parameter Size)。
最后,用有效参数规模除以模型的实际参数规模,就得到了该模型的能力密度。
对于混合专家模型(MoE)和量化模型,研究还引入了基于推理时间的密度定义。
这套定义综合考虑了内存访问时间和计算时间的影响,确保了不同架构模型之间具备可比性。
ChatGPT 的发布是一个明显的分水岭。
在此之前,模型密度的增长斜率较低;在此之后,斜率跃升了 50%。
资本的涌入和开源社区的繁荣共同加速了这一进程。
指数增长终有极限。
就像芯片制程受限于物理法则一样,大模型的致密律也面临信息论的理论上限。
每个参数能存储的比特数是有限的,类似于无损压缩算法无法将数据压缩到其熵值以下。
当算法优化接近这一物理极限时,增长将会放缓,届时需要量子计算或类脑计算等全新范式来突破瓶颈。
在此之前,致密律在相当长的一段时间内依然有效。
随着大模型开始具备自我科研的能力,甚至可能出现自我优化的加速循环。
致密律的发现标志着大模型竞争从军备竞赛转向了效率革命。
对于企业和开发者而言,依据 3.5 个月的翻倍周期精确预测未来的推理成本和模型能力,将成为制定技术战略的关键。
将强大的 AI 装进口袋的日子,已经触手可及。
参考资料:
https://www.nature.com/articles/s42256-025-01137-0
https://arxiv.org/pdf/2412.04315
END




















 11万+
11万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








