数据结构--ST表/树状数组（C++）

原创 已于 2025-05-09 17:09:11 修改 · 450 阅读 · 5 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #c++ #算法

于 2025-05-09 15:19:49 首次发布

目录

一、ST 表 && RMQ 问题

题目背景

题目描述

输入格式

输出格式

输入输出样例

说明/提示

代码展示：

二、树状数组

1.树状数组1

题目描述

输入格式

输出格式

输入输出样例

说明/提示

代码展示： 

2.树状数组2

输入格式

输出格式

输入输出样例

说明/提示

样例 1 解释：

 代码展示： 

一、ST 表 && RMQ 问题

题目背景

这是一道 ST 表经典题——静态区间最大值

请注意最大数据时限只有 0.8s，数据强度不低，请务必保证你的每次查询复杂度为 O(1)。若使用更高时间复杂度算法不保证能通过。

如果您认为您的代码时间复杂度正确但是 TLE，可以尝试使用快速读入：

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

函数返回值为读入的第一个整数。

快速读入作用仅为加快读入，并非强制使用。

题目描述

给定一个长度为 N 的数列，和 M 次询问，求出每一次询问的区间内数字的最大值。

输入格式

第一行包含两个整数 N,M，分别表示数列的长度和询问的个数。

第二行包含 N 个整数（记为 ai​），依次表示数列的第 i 项。

接下来 M 行，每行包含两个整数 li​,ri​，表示查询的区间为 [li​,ri​]。

输出格式

输出包含 M 行，每行一个整数，依次表示每一次询问的结果。

输入输出样例

输入 #1

8 8
9 3 1 7 5 6 0 8
1 6
1 5
2 7
2 6
1 8
4 8
3 7
1 8

输出 #1

9
9
7
7
9
8
7
9
说明/提示

对于 30% 的数据，满足 1≤N,M≤10。

对于 70% 的数据，满足 1≤N,M≤10^5。

对于 100% 的数据，满足 1≤N≤10^5，1≤M≤2×10^6，ai​∈[0,10^9]，1≤li​≤ri​≤N。

代码展示：
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
const int N = 1e6+10;
int f[N][21];
int a[N];
int n,m;
inline int read(int &x)
{
    x=0;
    int f=1;
    char ch=getchar();
    while(!isdigit(ch))
        {
            if(ch=='-')
                f=-1;
            ch=getchar();
        }
    while(isdigit(ch))
        {
            x=x*10+(ch-48);
            ch=getchar();
        }
    return x*f;
}
void ST_init()
{
    for(int i=1;i<=n;i++)
    f[i][0]=a[i];
    int t=log2(n)+1;
    for(int j=1;j<t;j++)
        for(int i=1;i<=n-(1<<j)+1;i++)
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
int query(int l,int r)
{
    int k=log2(r-l+1);
    return max(f[l][k],f[r-(1<<k)+1][k]);
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    read(n);
    read(m);
    for(int i=1;i<=n;i++)
        read(a[i]);
    ST_init();
    while(m--)
        {
            int a,b;
            read(a);
            read(b);
            cout<<query(a,b)<<endl;
        }
}

二、树状数组

1.树状数组1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

  • 将某一个数加上 x

  • 求出某区间每一个数的和

输入格式

第一行包含两个正整数 n,m，分别表示该数列数字的个数和操作的总个数。

第二行包含 n 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 m 行每行包含 3 个整数，表示一个操作，具体如下：

  • 1 x k 含义：将第 x 个数加上 k

  • 2 x y 含义：输出区间 [x,y] 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出 #1

14
16
说明/提示

【数据范围】

对于 30% 的数据，1≤n≤8，1≤m≤10；
对于 70% 的数据，1≤n,m≤10^4；
对于 100% 的数据，1≤n,m≤5×10^5。

数据保证对于任意时刻，a 的任意子区间（包括长度为 1 和 n 的子区间）和均在 [−2^31,2^31) 范围内。

样例说明：

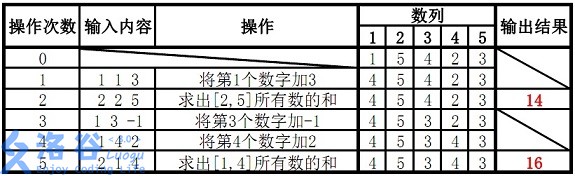
 故输出结果14、16

代码展示： 
#include<bits/stdc++.h>
#define lowbit(x) (x&(-x))
typedef long long ll;
const int N =5e5+10;
using namespace std;
int c[N];
int n,m;
ll ans;
void add_dandian(int x,int k)
{
	for(int i=x;i<=n;i+=lowbit(i))
	c[i]+=k;
}
int search(int begin,int end)
{
	for(int i=end;i;i-=lowbit(i))
	ans+=c[i];
	for(int i=begin-1;i;i-=lowbit(i))
	ans-=c[i];
	return 0;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		add_dandian(i,x);
	}
	for(int i=1;i<=m;i++)
	{
		int o,x,y;
		cin>>o>>x>>y;
		if(o==1)
		add_dandian(x,y);
		else
		{
			ans=0;
			search(x,y);
			cout<<ans<<endl;
		}
	}
}

2.树状数组2

如题，已知一个数列，你需要进行下面两种操作：

  1. 将某区间每一个数加上 x；

  2. 求出某一个数的值。

输入格式

第一行包含两个整数 N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含 N 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 M 行每行包含 2 或 4个整数，表示一个操作，具体如下：

操作 1： 格式：1 x y k 含义：将区间 [x,y] 内每个数加上 k；

操作 2： 格式：2 x 含义：输出第 x 个数的值。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

输出 #1

6
10
说明/提示
样例 1 解释：

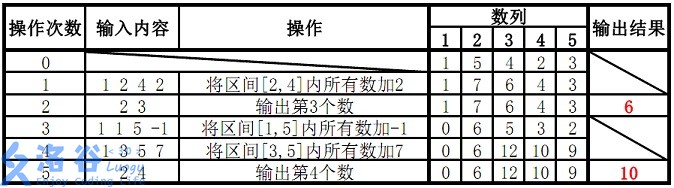
故输出结果为 6、10。

数据规模与约定

对于 30% 的数据：N≤8，M≤10；

对于 70% 的数据：N≤10000，M≤10000；

对于 100% 的数据：1≤N,M≤500000，1≤x,y≤n，保证任意时刻序列中任意元素的绝对值都不大于 2^30。

 代码展示： 
#include<bits/stdc++.h>
#define lowbit(x) (x&(-x))
typedef long long ll;
const int N =5e5+10;
using namespace std;
int a[N],d[N];
ll c[N];
int n,m;
void update(int pos,int k)
{
	for(int i=pos;i<=n;i+=lowbit(i))
	c[i]+=k;
}
ll ask_qujian(int pos)
{
	ll ans=0;
	for(int i=pos;i;i-=lowbit(i))
	ans+=c[i];
	return ans;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		d[i]=a[i]-a[i-1];
		update(i,d[i]);
	}
	for(int i=1;i<=m;i++)
	{
		int o,x,y,k;
		cin>>o;
		if(o==1)
		{
			cin>>x>>y>>k;
			update(x,k);
			update(y+1,-k);
		}
		else
		{
			cin>>x;
			cout<<ask_qujian(x)<<endl;
		}
	}
}

C++高级数据结构——ST表（倍增表）
lsy201009的博客
05-29 1828
今天我们所讲的叫做ST表，也被称为倍增表。ST表一般来说是用来处理“区间最值问题”（RMQ问题），就比如一个区间内的最大值、最小值之类的。
静态数据的快速处理：ST表解析与C++实现[模版题：P3865 【模板】ST 表 题解]
weixin_67247533的博客
04-16 2147
模版题：P3865 【模板】ST 表 题解]用于解决RMQ问题（Range Maximum/Minimum Query）;
c++数据结构——————st表：优化区间最值查询
qizhiburce的博客
10-23 316
就是分成了两个区间：[i,i+2^j-1]----->[i,i+2^(j-1)-1],[i+2^(j-1),i+2^j-1]状态转移方程为：st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);max(st[l][k],st[r-2^k+1][k])就是分解为两个长度相同的并且为2的次方长度的区间！可以分解为：[2,2+2^2-1],[7-2^2+1,7]的最大值（两个区间长度均为4，为2的次方）也就是max(st[2][2],st[7-4+1][2])
C++稀疏表（Sparse Table，ST表）区间最小值/最大值查询 模板
m0_66655785的博客
03-08 799
稀疏表（Sparse Table，ST 表）作为一种经典的数据结构，凭借其O (n log n) 的预处理时间复杂度和O (1) 的单次查询时间复杂度，成为解决这类问题的理想选择。
C++ ST表
struct_GS的博客
10-13 2060
RMQ 问题： RMQ（Range Minimum/Maximum Query）问题是指：对于长度为 n 的数列 A，回答若干询问 RMQ (区间 [ l，r ] )，返回数列A中下标在 l, r里的最小/大值，也就是说，RMQ 问题是指求区间最值的问题。 ST 表 st 表和线段树常被用来解决 RMQ 问题，两个各有优缺点：st 表运行效率高，但不能修改；线段树运行效率相对较慢，但支持修改操作。 st 表的合并复杂度为 O(1...
数列区间最大值-RMQ/线段树/树状数组
Lineng's blog
03-01 557
题目 输入一串数字，给你 M 个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。 输入格式 第一行两个整数 N,M 表示数字的个数和要询问的次数； 接下来一行为 N 个数； 接下来 M 行，每行都有两个整数 X,Y。 输出格式 输出共 M 行，每行输出一个数。 数据范围 1≤N≤1051≤N≤10^51≤N≤105, 1≤M≤1061≤M≤10^61≤M≤106, 1≤X≤Y≤N1≤X≤Y≤N1≤X≤Y≤N, 数列中的数字均不超过231−12^{31}−1231−1 Sol
//顺序查找 #include<iostream> #include<fstream> #include<string> #include <algorithm> using namespace std; #define MAXSIZE 10000 #define KEYSIZE 10//关键词个数 #define OK 0 #define ERROR -1 typedef string KeyType; typedef struct { KeyType key;//关键字域 int count;//词频 }ElemType; typedef struct { ElemType *R;//存储空间基地址 int length;//当前长度 }SSTable; //关键词列表 KeyType key[KEYSIZE] = {"little","prince","sheep","flowers","believe","stars","one","my","he","the"}; //初始化一个空的顺序表ST作为查找表 //要求顺序表ST的0号单元用作哨兵 int InitSSTable(SSTable &ST) { /*----------代码开始-------------*/ /*----------代码结束-------------*/ return OK; } //向查找表ST中尾插入关键词key //要求顺序表ST的0号单元用作哨兵 int InsertSSTable(SSTable &ST,KeyType key) { /*----------代码开始-------------*/ /*----------代码结束-------------*/ return OK; } //将形如""a"、"what?""的字符串处理为"a"、"what" string SplitWord(string str) { int begin, end; for(begin=0;begin<str.length();begin++) { if(str[begin]>='a' && str[begin]<='z') break; } for(end=str.length()-1;end>=0;end--) { if(str[end]>='a' && str[end]<='z') break; } if(begin<=end) return str.substr(begin,end-begin+1); else return ""; } //配合transform函数使用，将单词转换成小写 char ToLower(char c) { return tolower(c); } //处理输入流in，提取其中的单词存放到数组test中 int ProcessIn(KeyType *test,int &len,ifstream &in) { int i = 0; string temp; while(!in.eof()) { in>>temp; transform(temp.begin(), temp.end(), temp.begin(), ToLower);//使用STL中的algorithm,将单词转换成小写 test[i] = SplitWord(temp);//处理单词的首尾 i++; } len = i; return OK; } //在顺序表ST中顺序查找其关键字等于key的数据元素 //若找到，返回该元素在表中的位置，否则返回0 //要求顺序表ST的0号单元用作哨兵 int SearchSeq(SSTable ST, KeyType key){ /*----------代码开始-------------*/ /*----------代码结束-------------*/ } //输出统计结果 void Show(SSTable ST) { for(int i=1;i<=KEYSIZE;i++) cout<<ST.R[i].key<<":"<<ST.R[i].count<<endl; } int main() { ifstream in("testData/小王子.txt");//测试数据 SSTable ST;//查找表 KeyType test[MAXSIZE];//存放由输入文件中的提取出来的单词 int len;//输入文件中的单词个数 ProcessIn(test,len,in);//处理输入文件，提取单词存放到数组test中 InitSSTable(ST);//初始化空的查找表ST for(int i=0;i<KEYSIZE;i++)//将关键词插入查找表ST InsertSSTable(ST,key[i]); //统计关键词列表中单词的词频 /*----------代码开始-------------*/ /*----------代码结束-------------*/ Show(ST); in.close(); return OK; }补全代码
最新发布
11-26
我将补全顺序查找相关的C++代码，包括初始化顺序表、插入关键词、顺序查找和统计关键词词频等功能： ```cpp #include #include using namespace std; #define MAXSIZE 100 typedef struct { char key[20]; // ...
//折半查找 #include<iostream> #include<fstream> #include<string> #include <algorithm> using namespace std; #define MAXSIZE 10000 #define KEYSIZE 10//关键词个数 #define OK 0 #define ERROR -1 typedef string KeyType; typedef struct { KeyType key;//关键字域 int count;//词频 int index;//在关键词列表中的序号 }ElemType; typedef struct { ElemType *R;//存储空间基地址 int length;//当前长度 }SSTable; //关键词列表 KeyType key[KEYSIZE] = {"little","prince","sheep","flowers","believe","stars","one","my","he","the"}; //初始化一个空的查找表ST //ST的0号单元闲置不用 int InitSSTable(SSTable &ST) { /*-----------代码开始--------------*/ /*-----------代码结束--------------*/ return OK; } //向查找表ST中尾插入关键词key //ST的0号单元闲置不用，从1号单元开始插入 int InsertSSTable(SSTable &ST,KeyType key,int index) { ST.length++; /*-----------代码开始--------------*/ /*-----------代码结束--------------*/ ST.R[ST.length].index = index; return OK; } //将形如""a"、"what?""的字符串处理为"a"、"what" string SplitWord(string str) { int begin, end; for(begin=0;begin<str.length();begin++) { if(str[begin]>='a' && str[begin]<='z') break; } for(end=str.length()-1;end>=0;end--) { if(str[end]>='a' && str[end]<='z') break; } if(begin<=end) return str.substr(begin,end-begin+1); else return ""; } //配合transform函数使用，将'A'~'Z'转换成'a'~'z' char op(char c) { if(c>='A' && c<='Z') c = c+32; return c; } //处理输入流in，提取其中的单词存放到数组test中 int ProcessIn(KeyType *test,int &len,ifstream &in) { int i = 0; string temp; while(!in.eof()) { in>>temp; transform(temp.begin(), temp.end(), temp.begin(), op);//将单词转换成小写 test[i] = SplitWord(temp);//处理单词的首尾 i++; } len = i; return OK; } //在有序表ST中折半查找其关键字等于key的数据元素 //若找到，返回该元素在表中的位置，否则返回0 //ST的0号单元闲置不用，数据元素从1号单元开始存储 int SearchBin(SSTable ST,KeyType key) { /*-----------代码开始--------------*/ /*-----------代码结束--------------*/ return 0; } //输出统计结果 void Show(SSTable ST) { for(int i=1;i<=KEYSIZE;i++) cout<<ST.R[i].key<<":"<<ST.R[i].count<<endl; } //配合sort函数使用，对ST按关键词非递减有序进行排序 bool CmpKey(ElemType x,ElemType y) { return x.key < y.key; } //配合sort函数使用，对ST按关键词在关键词列表中的序号有小到大进行排序 //目的是为了输出顺序与给定的关键词列表顺序一致 bool CmpIndex(ElemType x,ElemType y) { return x.index < y.index; } int main() { ifstream in("testData/小王子.txt");//测试数据 SSTable ST;//查找表 KeyType test[MAXSIZE];//存放由输入文件中的提取出来的单词 int len;//输入文件中的单词个数 ProcessIn(test,len,in);//处理输入文件，提取单词存放到数组test中 InitSSTable(ST);//初始化空的查找表ST for(int i=0;i<KEYSIZE;i++)//将关键词插入查找表ST InsertSSTable(ST,key[i],i); sort(ST.R+1,ST.R+1+KEYSIZE,CmpKey);//对ST按关键词非递减有序进行排序 //统计关键词列表中单词的词频 /*-----------代码开始--------------*/ /*-----------代码结束--------------*/ sort(ST.R+1,ST.R+1+KEYSIZE,CmpIndex);//对ST按关键词在关键词列表中的序号有小到大进行排序 Show(ST); in.close(); return OK; }补全代码
11-26
4. **数据结构优化**： - 使用`vector`替代数组：`vector<ElemType> R;` - 自动内存管理，避免手动分配 ### 性能对比分析 | 查找方法 | 时间复杂度 | 空间复杂度 | 适用场景 | |---------------|------------|--...
树状数组 vs 线段树：数据结构选择终极指南
AI 算法实战派
07-04 1004
更新操作：某个同学的跳远成绩突然修正（单点更新）；查询操作：想知道1-10号同学的总分（区间查询），或者3-5号同学的平均分（复杂区间查询）。如果直接用普通数组存储成绩，每次查询1-10号的总分需要遍历10个元素（O(n)时间），如果有1000次查询，总时间就是1000×1000=1,000,000次操作——这在数据量大时会非常慢。这时候就需要更高效的数据结构。
C++树形结构(总）
Archie28的博客
07-25 1268
树形结构简介
ST表 C++
xcc134679的博客
10-18 419
将原始数据按照固定长度划分为若干个区间，以每个区间的最小元素作为该区间的代表值。然后，根据代表值的特点，利用动态规划的方式计算出每个区间段的最小值。构建好ST表后，可以进行各种区间查询操作，比如查询某个区间的最小值、最大值、平均值等。查询操作的时间复杂度为O(log n)，其中n为原始数据的长度。ST表的优势在于它的查询效率高，并且不需要额外的存储空间。它可以应用于各种区间查询问题，如最小值查询、最大值查询、区间和查询等。ST表是一种简洁、高效的数据结构，用于解决区间查询问题。
C++ST表
qq_41161266的博客
10-13 774
ST表是一种基于倍增思想的数据结构。常用来解决静态区间最值问题。ST表用于解决可重复贡献问题。例如有n个数的数列A，有m个区间，求区间[l,r]最大值。区间最大值是一个可重复贡献问题，所以可以对其进行预处理。对于这个问题我们能使用至多两个预处理过的区间来覆盖询问区间。设f[i][j]表示数列A中在[i,i+2^j-1]的最大值，即从第i个数开始2^j个数中的最大值。然后可以得到以下表达式：当需要求[l,r]最大值时，需要计算首先根据得接下来根据r−l+1<2^k+1得。
ST表（C++实现）
qq_61999856的博客
04-12 1236
ST表（C++实现）
st表C++模板
qq_62729874的博客
07-17 513
st表模板
ST表初识（C++）
qq_47982709的博客
08-15 2624
ST表:Sparse Table，稀疏表,一种数据结构，主要用来解决静态的区间最大/最小值问题。 主要思想：倍增思想。 在看ST表之前，先看一个问题： 2 4 1 5 3 在这个序列中找出区间【1,3】、【3,5】、【1,5】 max【1,3】= 4 max【3,5】= 5 max【1,5】= 5 大家可以发现，在区间【1,3】中最大值是4，区间【3,5】中最大值是5，在整个区间【1,5】中最大值是5，max(a,b) = max(max(a,c), max(c,.
C++算法进阶系列之倍增算法 ST 表
y6123236的专栏
09-15 1443
区间查询有很多方式，ST是不错的选择。
[c++算法] 一文带你搞懂倍增和st表！
doooge_awa的博客
01-18 1465
介绍倍增之前，我还需要介绍一下位运算。这一章很简单，如果你是dalao你也可以不看。倍增，顾名思义，即为成倍成倍的增加（一般是两倍两倍的增加）。比如说有一个数列a124816⋯a124816⋯，我们就可以说这个序列里的数是依次倍增的。所以，111倍增kkk次也就等于2k2^k2k。倍增在哪里能用的上呢？最明显的就是二进制。我们都知道，二进制的第iii位表示的是2i2^i2i，比如说数字131313位数333222111000。
洛谷3865-ST表模板-C++-（ST表+倍增）
DongLUOWAN的博客
03-16 1054
AC代码 关于这个代码，调了大半天，最后错在运算符优先级上，真的服了自己。 对于j+1<<(i-1)这一段语句，我原本想的是 j加上2^(i-1)， 但是运算的结果却是(j+1)^(i-1),导致代码一直出错。 😦 难受的一个晚上 希望在以后的代码过程中能够避免此类错误。 #include<iostream> #include<algorithm> #include<math.h> using namespace std; #define N 100010 #
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值