扩散概率模型作为一种新兴的研究方向,近年来在图像生成领域展现出了巨大潜力。追溯历史,基于扩散的生成模型在2015年就出现了,而直到2020年,Ho等人发表的论文Denoising Diffusion Probabilistic Models,DDPM,将扩散模型推向了大众,DDPM的出现使得扩散模型在实际应用中变得可行。本文将介绍DDPM的核心概念和技术,并以“flowers”数据集为例,从头开始训练DDPM,探索无约束条件下的图像生成过程。
在DDPM模型中,作者通过调整模型公式和训练流程,不仅提升了图像的“逼真度”,使其与生成对抗网络(GAN)相媲美,还验证了这些新型生成算法的可行性。
为什么需要生成模型
图像生成模型的主要任务是创造出与原始图像集相似的新图像,换句话说,就是生成能够“代表”这些图像的内容。我们之所以需要创建和训练生成模型,是因为,假设我们要生成256x256x3像素的图像,那么可以表示的所有可能图像的数量是庞大的。为了能够表达某种具体的、可理解的内容,图像的像素值必须按照特定的方式组合。

比如说,要让上面这张图像代表“向日葵”,图像中的像素必须有特定的正确的值。而能够包含这种图像的空间,其实只是所有可能的256x256x3图像集合中的一小部分。如果我们知道如何从这个子空间中采样出一个点,那我们就不需要构建“生成模型”了。不过,目前我们并不知道该如何做。😓
目前依然没有现成的捕捉或建模这个可能的数据子空间的概率分布,或者更准确地说,概率密度函数(PDF)的精确方法,且这个问题极有可能过于复杂,无法轻易理解。这也是我们需要“生成模型”的原因——它能帮助我们揭示数据背后潜在的似然函数。
注:PDF是“概率密度函数”,它描述的是连续随机变量的可能性分布——在这里,它指的是一个函数,表示图像在函数参数值的特定范围内出现的可能性。每个PDF都有一组参数,这些参数决定了分布的形状和概率。随着这些参数的变化,分布的形状也会随之改变。例如,正态分布的均值µ和方差σ²就决定了分布的中心位置和宽度。

高斯分布不同参数的影响
DDPM简介
扩散模型是一类受非平衡统计物理学启发的生成模型,核心思想是:
“我们可以通过马尔科夫链将一种分布逐步转化为另一种分布。” -- Deep Unsupervised Learning using Nonequilibrium Thermodynamics, 2015
扩散生成模型由两个对立的过程组成:正向扩散过程和反向扩散过程。
正向扩散过程:
“毁灭很容易,但创造很难” -- Pearl S. Buck
在正向扩散过程中,我们逐步向训练集中的图像添加噪声,使它们远离原本的结构。实现的方法是将原始图像所属的复杂分布转化为一个易于采样且易于理解的简单分布。正向扩散的结果是图像逐渐失去原有的特征,最终变得完全无法识别,数据的复杂分布被转化为一个简单的分布。所以正向扩散的过程的目标是实现数据分布的由难到易,由未知到已知的逐步转化。

反向扩散过程:

反向扩散的目标是逆转正向扩散过程。具体的做法是从一个简单的噪声图像开始,逐步逆转其所经历的噪声添加过程。从简单空间(或者说是已知分布的空间)开始的好处是,我们知道如何从这个空间采样一个点,并以此作为反向过程的起点。然后让这些“简单”空间中的点回到原始数据分布所在的子空间。
问题在于,虽然可以从任何一个简单空间中的点出发,但只有其中一小部分路径能成功引导我们回到数据子空间。所以在反向扩散中需要借鉴正向扩散过程中的小步骤,才能准确恢复数据。具体的做法是:反向扩散过程的每一步都在使用深度学习预测正向过程中的PDF参数,最终从噪声图像恢复出清晰的图像。

这种训练和生成新样本的方法,比GANs更加稳定,并且优于传统的变分自编码器(VAE)和归一化流等方法,所以自2020年提出以来,DDPM成为了许多前沿图像生成系统的基础,如DALL-E 2、Imagen、Stable Diffusion和Midjourney等。
DDPM的数学原理
这一部分将尽可能的通俗易懂的介绍理解DDPM所需的数学内容。首先,来看一下DDPM的正向和反向扩散过程的图示:

中间的箭头上有两个重要术语:
-
正向扩散核FDK。它表示在正向扩散过程中,给定时间步时的图像,如何得到时间步t的图像的概率分布PDF。它即是在正向扩散过程中每个步骤应用的“转移函数”。
-
反向扩散核RDK。它表示在已知时间步的图像的情况下,时间步的图像的概率分布。参数θ表示反向过程的分布是由神经网络学习得到的,θ是神经网络的参数。RDK是反向扩散过程中每个步骤应用的“转移函数”。
正向扩散过程的数学原理

在去噪扩散概率模型(DDPM)中,正向扩散过程的分布由下面的马尔科夫链来定义:

我们从数据集中随机选取一张图像。数学上来说,这等同于从原始(但未知的)数据分布中采样:。 正向扩散过程的PDF是从时间步1到T的每一时刻的分布的乘积。从时间步1到T的所有中间噪声图像称为“latents”,这些latents的维度与原始图像相同。
正向扩散过程是固定且已知的。定义正向扩散核(FDK)使用的PDF是高斯分布,如下面的公式所示:
![]()
在每个时间步,定义图像的分布的参数为:
-
均值:

-
方差:

这里的β是“扩散率”,通过“方差调度器”进行预计算,I是单位矩阵。在每个时间步,原始图像都会被添加高斯噪声,噪声的量由调度器控制。通过选择足够大的时间步并设置一个合理的调度,正向扩散核会逐渐将数据分布转换成接近各向同性高斯分布。
那么,该如何从Xt-1获得Xt,以及每个时间步是如何添加噪声的呢?
这个问题可以通过变分自编码器中的重参数化技巧来帮助理解。根据公式(2),我们可以轻松地从正态分布中采样出图像:

其中,ϵ 是从标准高斯分布中随机采样得到的噪声项,经过缩放后添加到上。通过这种方式,从初始图像开始,图像会在每个时间步到中逐步加入噪声。
在实际的实现过程中,DDPM 的作者使用了一个“线性方差调度器”,将 β设置在[0.0001, 0.02]的范围内,总时间步数设置为1000。作者在论文中指出“DDPM通过每一步正向过程(通过 因子)缩小数据,以防止在添加噪声时方差过大。”下图展示了随着时间步数的增加,β的变化情况。

Variance Scheduler vs timesteps
但是这种方式存在一个效率问题 🐢。
每当我们在时间步采样一个潜变量时,我们必须执行步马尔可夫链操作。

在目前的正向扩散核公式中,我们不得不经过马尔可夫链的所有步骤才能得到。换句话说,必须经过所有的个中间状态,才能从原始图像获得目标图像。
为了解决这个问题,DDPM的作者修改了扩散核公式,使其可以直接从时间步0(即原始图像)跳到时间步。

在DDPM中,修改后的正向扩散核公式可以让我们跳过所有中间时间步。为了实现这一点,引入了两个新的术语:

其中αt用来调整正向扩散核的过程,公式(5)表示从1到t的α的累积乘积。通过将β替换为α,并利用高斯分布的加法性质,正向扩散过程可以用α来重新表示:

🚀 使用公式(6),我们可以在马尔可夫链中的任何时间步进行采样。这就是正向扩散过程的改进方式。
反向扩散过程的数学细节
在反向扩散过程中,我们的目标是逆向执行正向扩散过程的步骤。反向扩散过程的任务是学习在有限的时间内(个时间步)逆转正向扩散过程。”这就意味着我们要逐步“撤销”正向过程的操作,也就是逐步去除在正向过程中加入的噪声。这个过程通过神经网络模型来实现。
在正向过程中,转移函数是基于高斯分布定义的,那么对于反向过程 ,我们应该使用什么函数呢?神经网络需要学习什么呢?
1949年,W. Feller证明了,对于高斯分布(以及二项分布),扩散过程的反向过程与正向过程具有相同的数学形式。也就是说,就像正向扩散核(FDK)使用正态分布一样,我们也可以使用相同的高斯分布形式来定义反向扩散核。反向扩散过程同样是一个马尔可夫链,神经网络在每个时间步会预测反向扩散核的参数。
在训练过程中,神经网络学习到的参数估计值应该接近正向扩散核后验的参数。这样做的目的是,如果我们按照正向过程的反向路径进行操作,最终有可能回到原始的数据分布。这也意味着我们可以学习如何从纯高斯噪声出发,生成与训练数据分布高度匹配的新样本(从纯高斯分布出发是因为在推理过程中,我们无法访问正向过程的具体细节)。

反向扩散的马尔可夫链从正向扩散结束的地方开始,即从时间步开始,此时数据分布已经转化为(接近)各向同性的高斯分布。

反向扩散过程的概率密度函数(PDF)是对所有可能路径的“积分”,这些路径表示从纯噪声出发,经过多次步骤,最终返回到一个与原始数据分布相同的样本。


DDPM的训练目标和损失函数
基于扩散的生成模型的训练目标是:最大化反向过程结束时生成样本属于原始数据分布的对数似然。
扩散模型中的转移函数服从高斯分布。为了最大化高斯分布的对数似然,我们需要找到高斯分布的参数,使得生成的数据尽可能符合原始数据的分布。
为了训练神经网络,我们定义损失函数为目标函数的负值(最小化损失函数也就是最大化负的似然函数)。也就是说,越大,损失越小,反之亦然。
事实上,这个目标无法直接计算,因为我们需要在连续值个时间步中对一个非常高维的像素空间进行积分。因此,DDPM的作者借鉴了变分自编码器(VAE)的思想,使用变分下界(VLB)(也就是Evidence lower bound,ELBO)重新构建了训练目标,这个方程看起来非常复杂👻:

在上面的公式的基础上做一些简化后,DDPM 的作者得出了最终的变分下界损失项:

将上述损失项拆分到每个时间步,我们可以看到:

分解后的 ELBO 方程,以便理解其中每个部分对应扩散过程中的哪个时间步。 可能你会觉得这个损失函数非常庞大!但 DDPM 的作者进一步简化了它,通过忽略一些项来得到更简洁的损失函数。
被忽略的项包括:
LO—— 去掉后反而得到了更好的结果。
LT—— 是正向过程最终潜变量和反向过程初始潜变量之间的“KL 散度”。但因为这里没有神经网络参数参与,除了定义好的方差调度器并使用大时间步长,我们无能为力,只有这样才能确保两者都是各向同性的高斯分布。 最终,Lt-1成为唯一的损失项,它是正向过程后验和反向过程参数化分布之间的 KL 散度。两者都是高斯分布。
在忽略了某些项后,去噪扩散概率模型(DDPMs)中,我们只需要最小化正向后验和反向过程之间的KL散度。

项被称为“正向过程后验分布”。
神经网络在训练时的任务是近似/估计这个高斯后验的参数,使得 KL 散度最小。

后验分布的参数如下所示:

为了简化任务,作者决定将方差固定为常数。
这样,模型只需要学习预测上述方程,反向扩散核就会被修改为:

因为我们已经将方差固定为常数,最小化 KL 散度就变成了最小化两个高斯分布和(例如,上图左边图中均值的差异)之间均值()的差距,这可以通过以下方式实现:
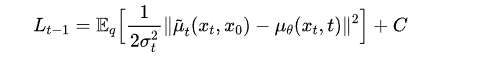
ELBO 损失项变成了两个分布“均值”之间的平方差。 我们有三种方法来进行预测:
-
直接预测x0,并使用后验函数中计算均值μ。
-
预测整个均值项μ。
-
预测每个时间步的噪声,可以通过使用重参数化技巧,将均值μ中x0用xt来表示。
选择第三种方法并进行简化后,可以表示为:
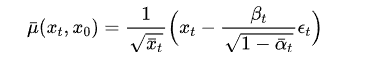
同样地,可以写为:

在训练和推理的阶段,我们知道βt αt,和xt,因此模型执行需要每一个时间步的噪声即可。所以简化之后的DDPM的损失函数如下:

我们得到了最终的损失函数,它实际上就是:去噪扩散概率模型(DDPMs)中的“均方误差”,它表示的是正向过程中添加的噪声与模型预测的噪声之间的差异。这是 DDPM 论文中的最关键贡献之一,因为从复杂的 ELBO 项开始,我们最终得到了机器学习领域最简单的损失函数!




















 395
395

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








