HIR-Diff 深度解析：用改良扩散模型做无监督高光谱图像恢复（CVPR 2024）

最新推荐文章于 2025-11-24 18:29:32 发布

原创最新推荐文章于 2025-11-24 18:29:32 发布 · 666 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #计算机视觉 #深度学习

遥感图像同时被 2 个专栏收录

7 篇文章

订阅专栏

图像恢复

4 篇文章

订阅专栏

原论文：Pang et al. – “HIR-Diff: Unsupervised Hyperspectral Image Restoration via Improved Diffusion Models”, CVPR 2024

作者：Li Pang, Xiangyu Rui, Long Cui, Hongzhong Wang, Deyu Meng, Xiangyong Cao;
项目开源链接：LiPang/HIRDiff

一、引言

高光谱图像（Hyperspectral Image, HSI）凭借其丰富的光谱维度，在遥感监测与环境分析等任务中有着明显优势。然而，这类数据在实际采集中往往会受到噪声、模糊、条带、缺失和低分辨率等多种退化因素影响，导致恢复任务成为高光谱应用链条中的关键步骤。尽管基于深度学习的恢复方法近年来取得了显著进展，但在数据获取、泛化能力及计算复杂度等方面仍存在一定限制。例如，高光谱领域缺乏成对训练数据，不同传感器间的光谱差异也会影响模型迁移，而高维度结构会进一步提高模型设计与训练的成本。

扩散模型（Diffusion Models）在图像生成与复原任务中具备较强的先验建模能力，因此自然被视为潜在的高光谱恢复工具。但直接将现有扩散模型用于高光谱图像并不现实。一方面，扩散模型普遍基于 RGB 或少数波段训练，无法与高光谱的高维结构直接适配；另一方面，若对数十到数百个波段逐一执行扩散过程，计算量将成倍增加。此外，高光谱图像通常具有明显的空间-光谱耦合特性，仅延用 RGB 图像的扩散模型结构并不能充分利用这些特征。

在这种背景下，CVPR 2024 的 HIR-Diff 提出了一个结构上较为直接的解决方案，即基于高光谱数据的低秩特性，将高光谱图像分解为两个部分：一个包含少量通道的降维图像 A，以及一个描述光谱映射关系的系数矩阵 E。E 可以利用 SVD 与 RRQR 等线性代数工具从观测数据中直接估计，而降维后的图像 A 则交由预训练扩散模型进行恢复。通过三阶张量乘法 A ×₃ E，即可重建完整的高光谱图像。相比直接在高维空间执行扩散，这种方式减少了维度差异带来的结构不匹配，同时也显著降低了恢复过程的计算开销。

为了进一步提升推理效率，论文引入了 指数噪声调度（Exponential Noise Schedule），使扩散模型在少量采样步数下仍能保持稳定的重建质量。这类改动侧重于提高推理效率，使得扩散模型在高光谱恢复任务中变得更实用。

整体来看，HIR-Diff 并不是提出一种全新的生成模型，而是重点关注如何将扩散模型合理地应用于高光谱领域。其核心贡献在于将低秩分解与扩散先验结合，使恢复过程既不依赖训练，又能够有效降低高维光谱带来的计算负担。本文将在后续部分对其方法设计、关键思想及潜在局限展开更系统的分析。

二、方法框架概述

HIR-Diff 的核心思路可以概括为：利用高光谱数据在光谱维度上的低秩特性，将恢复过程拆解为光谱结构的线性估计与空间结构的扩散建模两个部分。具体而言，方法首先基于退化观测图像估计光谱系数矩阵 E；然后在降维空间中使用预训练扩散模型恢复降维图像 A；最后再通过张量乘法 A ×₃ E 重建完整的高光谱图像。整体流程在概念上相对直接，但每个步骤都涉及较为关键的设计选择，使得扩散模型能够有效应用于高维的高光谱场景。

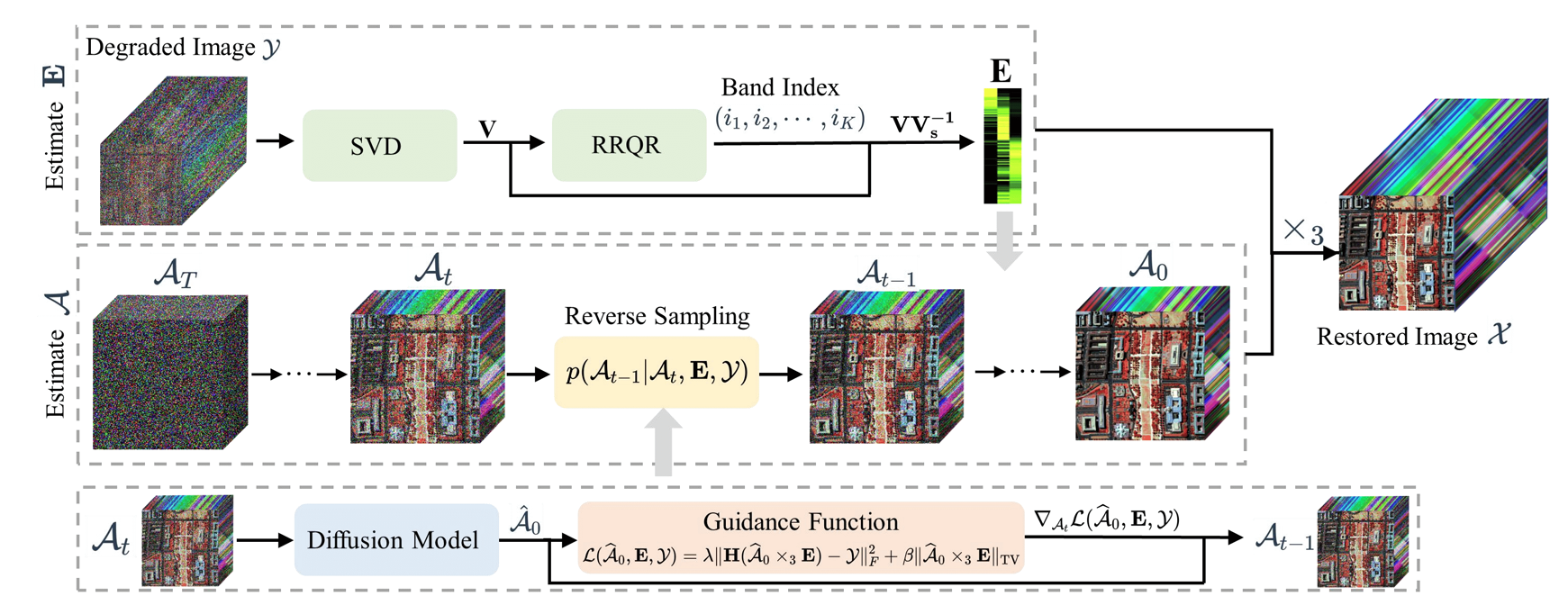
在输入为退化高光谱图像 Y 的情况下，HIR-Diff 的处理过程可分为三个主要阶段（如上图）：

（1）光谱系数矩阵 E 的估计（SVD + RRQR）
基于高光谱图像光谱维度的低秩性质，作者使用 SVD 提取光谱主方向，并进一步采用 RRQR 选择更具代表性的波段，实现对系数矩阵 E 的稳健估计。这一过程完全基于线性代数，不依赖任何训练数据或模型。

（2）降维图像 A 的扩散恢复
在 E 固定后，高光谱恢复被简化为“恢复 K 通道的降维图像”问题。作者采用预训练的遥感扩散模型，通过噪声反演与梯度引导，使生成的 A 满足观测约束并呈现较好的空间结构。由于 A 的通道数远小于原始波段数，该步骤避免了直接在高维光谱空间中运行扩散模型的高计算代价。

（3）基于 A ×₃ E 的高光谱重建
当 A 被恢复后，通过三阶张量乘法即可得到完整的重建图像 X。由于 E 描述光谱方向的低维结构，而 A 捕获了空间结构，因此两者结合形成的重建保持了高光谱图像应有的光谱一致性与空间细节。

从整体结构来看，HIR-Diff 并未试图将扩散模型扩展到高光谱维度，而是通过分解策略将任务拆解，使扩散模型在一个与其训练域更接近的空间中工作。这样的设计既利用了扩散模型的空间先验能力，又规避了高光谱数据维度不匹配的问题，使得方法保持一定的简洁性。

2.1 系数矩阵E的估计

HIR-Diff 的第一步是从退化高光谱图像 Y中估计光谱系数矩阵 E。这一矩阵用于描述完整高光谱图像X的光谱方向结构，使得 $X = A \times_3 E$ 成立。论文的关键观点是：即使图像退化，光谱维度仍保持强相关性，因此可以利用 SVD 在噪声存在时提取稳健的光谱子空间，再从该子空间导出系数矩阵 。

为了做到这一点，作者引入两个步骤：先用 SVD 估计光谱子空间，再用 RRQR 选择代表性波段（band index），最终通过闭式解构建 E。

（1）为什么可以用 SVD？——利用退化图像的低秩结构

高光谱图像具有强光谱相关性，按照论文表述，这意味着 HSI 在光谱维度呈现“低秩”特性，即多数光谱变化可以被少量主方向描述。因此，即便输入 Y是噪声污染后的图像，其主要光谱结构仍可以通过对 Y做 SVD 提取。

论文将Y展平为 $Y_{(3)}$ 后，进行 rank-K SVD 分解：

$Y_{(3)}^T = (US)V^T$

其中：

U：空间结构（空间维度展开）
S：奇异值（能量分布）
V：光谱方向（主成分方向）

SVD 的关键特性是正交性与噪声鲁棒性：

正交性使不同光谱方向互不干扰（列向量独立），适合作为光谱基底。
噪声鲁棒性意味着右奇异向量 V不容易受到独立噪声干扰（论文也明确指出这一点：SVD 有“noise-robust”性质）。

直观解释：
即便高光谱每个波段都含有噪声，但噪声在光谱维是“无结构的随机扰动”，而 SVD 会将这种无结构噪声排在较低奇异值位置，因此前 K 个奇异向量仍能代表真实光谱变化。

（2）E 是怎么从 SVD 得到的？——通过子矩阵逆构建光谱映射

论文定义降维图像 A为原图中若干波段，其波段索引为 $(i_1, i_2, \dots, i_K)$ ，对应于 SVD 中 V 的行向量组合：

$V_s = [v_{i_1}, v_{i_2}, \dots, v_{i_K}]^T$

然后利用以下关系推导系数矩阵：

首先分解降维图像A：

$\mathbf{A}_{\mathbf{Y}(3)}^{\mathrm{T}} = (\mathbf{U S}) \mathbf{V}_{\mathbf{s}}^{\mathrm{T}}$

那么将对应目标Y分解后，得到的US替换为上述的A表达：

$\mathbf{Y}_{(3)}^{\mathrm{T}} = \mathbf{A}_{\mathbf{Y}(3)}^{\mathrm{T}} (\mathbf{V}_{\mathbf{s}}^{\mathrm{T}})^{-1} \mathbf{V}^{\mathrm{T}}$

也就等价于：

$\mathcal{Y} = \mathcal{A}_{\mathbf{Y}} \times_3 (\mathbf{V} \mathbf{V}_s^{-1})$

最终，结合 $\bar{\mathcal{Y}} = \mathbf{H}(\mathcal{X}) = \mathbf{H}(\mathcal{A} \times_3 \mathbf{E}) = \mathbf{H}(\mathcal{A}) \times_3 \mathbf{E} = \bar{\mathcal{A}}_{\mathbf{Y}} \times_3 \mathbf{E}$ 可得到 $\mathbf{E} = \mathbf{V} \mathbf{V}_s^{-1}$ 。

为什么这个公式成立？论文给出如下推理：

SVD 给出了观测图像 Y的主光谱方向（矩阵 V）
假如 clean 图像 X同样具有相同的光谱方向（或非常接近），那么光谱基底也应是 V
降维图像 A仅保留这 K 个光谱方向对应的波段，因此需要一个映射矩阵 E将其扩展到完整 B 维
而这个映射刚好可以由 V与子矩阵 $\mathbf{V}_s$ 之间的线性关系闭式表达，因此 $\mathbf{E} = \mathbf{V} \mathbf{V}_s^{-1}$ 。

更直观的解释：

V是 B 维空间里的 K 个主方向。
降维图像 A相当于从原始数据中挑出的 K 个“特征波段”。
那么，只要我们知道“这些波段的坐标在 V基底中的表示”，就能恢复全部波段。
由此，矩阵 E就承担了“把降维图像重新扩展回 B 维”的作用。

也就是说：

SVD 提供光谱基底，Vs提供所选波段的系数，因此 $\mathbf{E} = \mathbf{V} \mathbf{V}_s^{-1}$ 是将 A 映射回完整光谱空间的自然构造。

（3）为什么还要用 RRQR？——解决谱带选择导致的数值不稳定问题

构造 E需要 $\mathbf{V}_s^{-1}$ 存在，而这要求 $\mathbf{V}_s$ 是非奇异（可逆）的。

但论文指出：

如果随便选 K 个波段， $\mathbf{V}_s$ 很可能高度相关，行列式极小，导致 E 数值极端不稳定

原因是：
高光谱数据具有强相关性，邻近波段内容非常相似。
如果挑的波段“信息重复”， $\mathbf{V}_s$ 就会变得接近奇异，逆矩阵会非常大，导致数值爆炸，最终影响扩散模型恢复 A 的稳定性。

RRQR（Rank Revealing QR）的作用在于：

在矩阵 V 的列中寻找 最具独立性 的 K 列
最大化行列式 $|\det(\mathbf{V}_s)|$ ，使 $\mathbf{V}_s$ 尽量远离奇异
从而确保 $\mathbf{E} = \mathbf{V} \mathbf{V}_s^{-1}$ 的数值稳定性
也确保所选波段在内容上充分“不重复”、代表性更强

论文的实验结果也证明：
无 RRQR 时，恢复 PSNR 会显著下降，而使用 RRQR 后性能显著提升。

直观理解：

RRQR 不是随便选 K 个波段，而是挑出“最有代表性、最不相似”的 K 个波段，从而保证 E 的稳定与有效性。

2.2 降维图像 A 的扩散恢复

在系数矩阵 EEE 被估计之后，高光谱恢复问题被拆解为空间域的降维图像 $\mathcal{A} \in \mathbb{R}^{H \times W \times K}$ 的重建。此时的关键任务是：如何利用扩散模型在低维空间获得与观测一致的 A，使其在空间结构上尽可能接近干净图像。HIR-Diff 的核心思想是在降维空间而非完整光谱空间运行扩散模型，使其专注于恢复空间结构，同时避免在高维光谱域中建模的巨大计算开销。

（1）设计动机：为什么扩散模型放在 A 空间而非 X 空间？

在设计上，作者并未直接对完整高光谱图像 X 进行扩散反演，而选择在降维图像 A 上应用预训练扩散模型。这一决定源于三个方面的考虑。

首先，高光谱图像的光谱维度通常有数十甚至上百个通道，远超扩散模型的典型训练域（例如 RGB 的 3 通道）。直接将扩散模型扩展至如此高维空间不仅需要大量高光谱训练数据，也会显著增加模型的结构设计难度。因此，将问题约化至 K 通道的降维图像 A，可以让扩散模型工作在一个更加“正常”的通道规模上。

其次，降维后的 A 仍保留了完整的空间结构，而扩散模型在空间纹理恢复方面具有优势。扩散模型通过反向采样可重建纹理、边缘、局部结构等空间细节，这恰好是高光谱恢复中最难依靠线性方法完成的部分。让扩散模型专注空间维度，避免其尝试“学习高光谱光谱规律”，是合理的职责划分。

此外，光谱一致性并不由扩散模型负责，而由先验计算得到的系数矩阵 E 约束。只要 A 被合理恢复，完整光谱图像可通过张量乘法 A×3EA \times_3 EA×3E 得到。这意味着扩散模型不用学习复杂的光谱映射，从而减轻了模型负担，使得预训练模型在新的任务中更容易适配。

（2）恢复过程：扩散模型的反向采样与数据一致性引导

在 HIR-Diff 中，降维图像 AAA 的恢复依赖于扩散模型的反向采样过程。论文中采用了条件扩散框架（Conditional Diffusion）来引导 A 的生成，其核心公式为：

$\hat{\epsilon} = \epsilon_\theta(A_t, t) - s(t)\nabla_{A_t}\mathcal{L}(A_t)$

其中 $\epsilon_\theta(A_t, t)$ 表示扩散模型对噪声的预测， $\mathcal{L}(A_t)$ 是条件引导损失：

$\mathcal{L}(A_t) = \lambda\|H(A_t \times_3 E) - Y\|_2^2 + \beta\,\text{TV}(A_t \times_3 E)$

这里：

H为退化算子，例如模糊、下采样或缺失掩码；
TV(⋅)是全变差正则项，用于约束空间平滑性；
λ与 β分别控制数据一致性与空间平滑的权重；
s(t) 是随时间变化的步长调节系数。

随后，扩散模型按 DDPM / DDIM 的采样公式生成下一步状态：

$A_{t-1} = \frac{1}{\sqrt{\alpha_t}}\left(A_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}}\hat{\epsilon}\right) + \sigma_t z$

其中：

$\alpha_t, \bar{\alpha}_t$ 为噪声调度参数（论文 Sec. 3.4）；
$\sigma_t$ 控制随机噪声注入强度；
$z \sim \mathcal{N}(0, I)$ 为标准高斯噪声。

这一流程在每一步迭代中重复，逐步去除噪声并引入条件引导，使生成的降维图像 A 在满足观测一致性的同时，具备合理的空间结构。通过这种方式，扩散模型可以在降维空间有效恢复图像，而不必直接在高维光谱空间中进行操作。

论文指出，使用该条件引导方法能够同时兼顾：

空间结构的自然性：扩散模型学习的先验保证了生成图像纹理与边缘合理；
数据一致性：梯度引导确保 A ×₃ E 在经过退化算子 H 后尽量接近观测 Y；
数值稳定性：指数噪声调度结合小步长更新使得少步采样仍能保持恢复质量。

（3）方法可行性的原因：为何扩散模型能在降维空间有效工作？

这种在降维空间运行扩散模型的方式之所以有效，可以从三个角度说明其可行性。

首先，K 通道的 A 相较于原始高光谱图像维度更低，但其空间结构完全保留。换言之，它仍然是“空间结构丰富的图像”，而扩散模型正是擅长学习这类图像的自然统计特性。因此，即便降维过程使 A 的光谱信息压缩了，但对扩散模型而言，它仍然是一个合法且可恢复的图像对象。

其次，光谱重建由 E 完成，而 E 来自光谱主方向的子空间估计。扩散模型并不会改变光谱映射，只调整空间细节。因此，模型不必承担跨光谱通道推理的任务。扩散模型的能力被限定在它擅长的领域：空间域的统计建模。

最后，数据一致性约束在整个采样过程中持续施加，避免模型在追求“图像自然性”时偏离观测数据。特别是在严重退化或缺失较多像素的情况下，该约束能有效引导采样轨迹，使恢复结果保持物理一致性。事实上，论文在消融实验中给出了数据一致性提升效果的量化证明。

综合来看，将扩散模型置于降维空间，而不是完整高光谱空间，是一种兼具可行性与效率的策略：

维度降低使模型可以复用；
光谱重建交由 E 保证；
空间细节通过扩散过程补全；
数据一致性使结果不会偏离观测。

这种“分而治之”的策略构成了 HIR-Diff 的核心优势之一。

2.3 指数噪声调度

在 HIR-Diff 的降维图像 AAA 恢复过程中，噪声调度是影响扩散采样速度与最终重建质量的重要因素。论文指出，传统的线性或余弦噪声调度在条件引导下往往存在两个问题：前期噪声下降过慢，导致需要大量采样步数才能接近干净图像；后期步长变化过快，则可能影响细节的精修。这使得在实际工程应用中，扩散恢复的计算开销较大。

为解决这一问题，作者提出了 指数噪声调度，其核心思路是让噪声在前期快速衰减、在后期缓慢下降，从而在少量采样步数下仍能保持较高恢复质量。

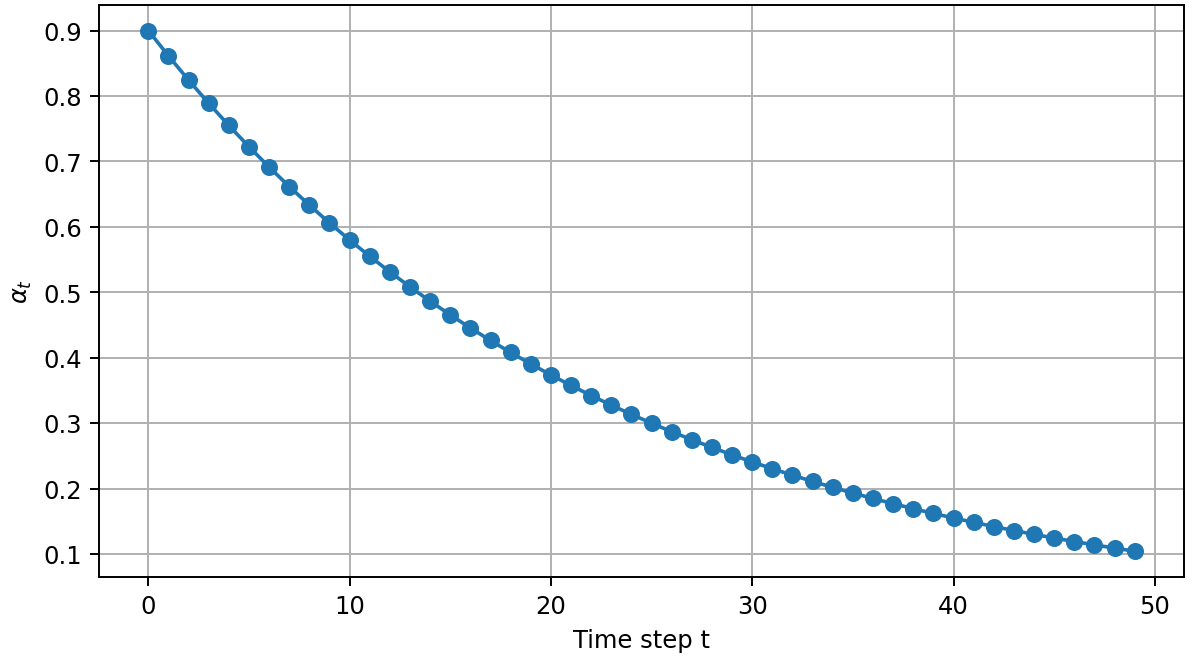
论文给出的公式为：

$\alpha_t = \alpha_{\min}^{\frac{t}{T}} \cdot \alpha_{\max}^{1-\frac{t}{T}}, \quad \bar{\alpha}_t = \prod_{i=1}^t \alpha_i$

其中 $\alpha_{\min}$ 与 $\alpha_{\max}$ 分别控制噪声的最小值与最大值，而 $\bar{\alpha}_t$ 表示累计噪声比例。通过这种设计，扩散模型在前几步就可以快速去除高强度噪声，使生成的图像迅速接近目标分布，而后期缓慢衰减有助于精修纹理和细节。

这种调度策略的有效性主要体现在三个方面。首先，它能够 加速采样，在少量步骤下达到与传统线性调度相近的恢复效果。其次，它保持了 后期生成的稳定性，确保细节和空间结构不会因步长过大而丢失。最后，它与条件引导相互配合，使扩散模型在低维空间恢复 A 时，既遵循自然图像的空间先验，又满足观测一致性和 TV 正则约束。

在反向采样过程中，指数噪声调度直接作用于每步更新公式：

$A_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( A_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \hat{\epsilon} \right) + \sigma_t z$

其中 $\hat{\epsilon}$ 是经过条件引导调整后的噪声预测， $\sigma_t z$ 为注入的随机噪声。通过调整 $\alpha_t$ 的指数衰减，HIR-Diff 可以在少步采样下快速降低噪声，同时保证生成的 A 在空间结构上保持自然且与观测数据一致。

总的来说，指数噪声调度使扩散模型的推理过程更加高效和稳定，是 HIR-Diff 能在 20 步左右完成高质量恢复的关键设计之一，同时也体现了作者在工程实践中对采样策略的优化考虑。

三、实验设计

为了全面评估 HIR-Diff 的性能，论文设计了一系列实验，不仅关注恢复结果的量化指标，还分析了方法在不同退化类型和数据集上的表现规律。

3.1 数据集选择

论文选择了多个高光谱数据集，包括 Salinas、WDC 和 Houston，覆盖农业、城市和混合地物场景。

3.2 评价指标

为了量化恢复效果，实验采用了两种常用指标：峰值信噪比（PSNR）和结构相似性指数（SSIM）。PSNR 用于衡量恢复图像与原图的像素差异，而 SSIM 用于评估图像结构信息的保留情况。

3.3 对比实验

实验涵盖了 HSI 恢复的三类典型任务：去噪、超分辨率和缺失像素修复。为全面评估 HIR-Diff 的性能，选择了多类对比方法：

模型驱动方法：如 BM4D、NGMeet、ETPTV，这类方法依赖手工设计的先验，具有较好的泛化能力，但在复杂场景下受限于先验表达能力；
监督深度学习方法：如 T3SC、MACNet、SST、SERT，需要大量标注数据训练，容易在未知数据上泛化不足；
无监督深度学习方法：如 DDS2M、DIP2d/3d，无需额外标注数据，能够在不同数据集间自适应，但计算开销较大。

通过这样的设计，可以观察 HIR-Diff 在不同任务和条件下相对于现有方法的优势。

（1）去噪对比

去噪实验在 WDC mall、Houston 和 Salinas 数据集上进行，分别添加标准差为 30、50、70 的高斯噪声，对比了传统方法（BM4D、NGMeet、ETPTV）、监督深度学习方法（T3SC、SST、SERT）以及无监督方法 DDS2M。

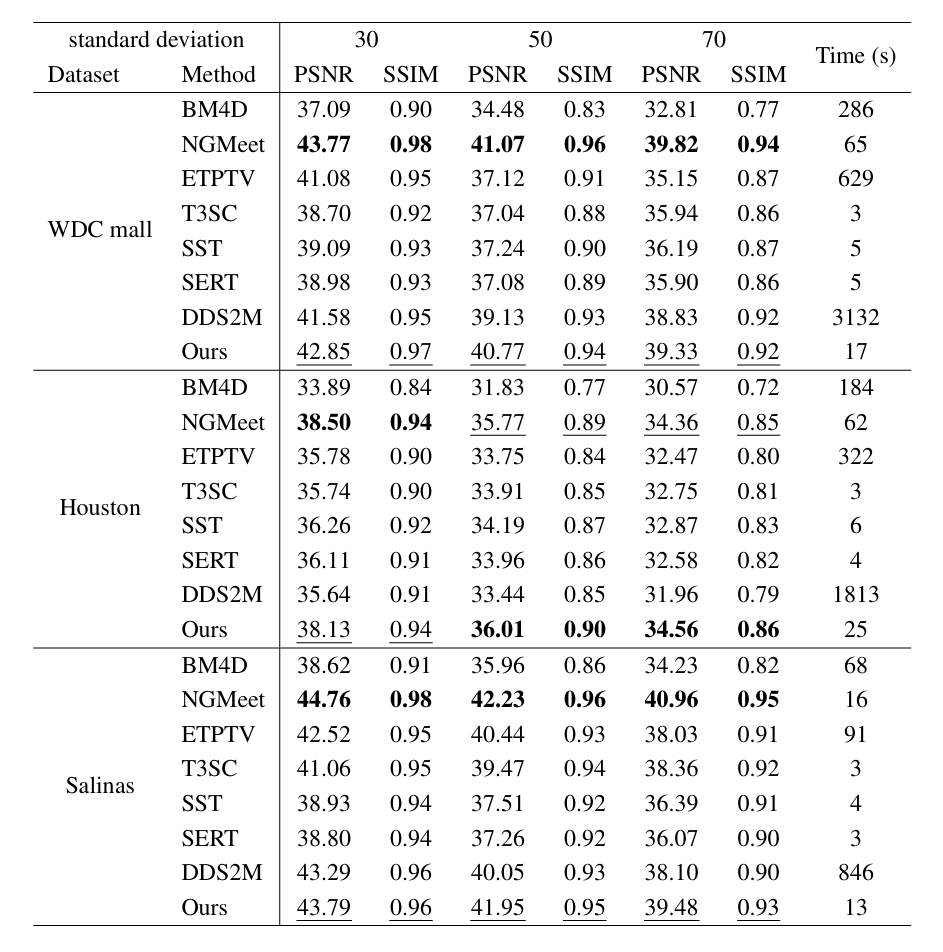
实验结果显示，HIR-Diff 在大多数情况下能够提供较高的恢复质量，例如在 WDC mall 数据集标准差为 50 时，PSNR 达到 40.77，SSIM 为 0.94，相比 BM4D 提升明显，同时运行时间仅 17 秒，远快于 DDS2M 的 3132 秒。

然而，NGMeet 的 PSNR 在大多数条件下略高于 HIR-Diff（Ours），说明在纯噪声去除的定量指标上，NGMeet 仍具有一定优势。尽管在 PSNR 指标上略低，HIR-Diff 在运行效率上具有显著优势。例如，在 WDC mall 数据集上，标准差为 50 的情况下，NGMeet 需要约 65 秒，而 HIR-Diff 仅需 17 秒即可完成推理。同时，HIR-Diff 在其他任务如超分辨率和缺失像素恢复中表现优异，显示出更全面的适用性。

（2）超分辨率对比

超分辨率实验主要考察含噪高光谱图像在 ×2、×4、×8 缩放下的恢复效果。

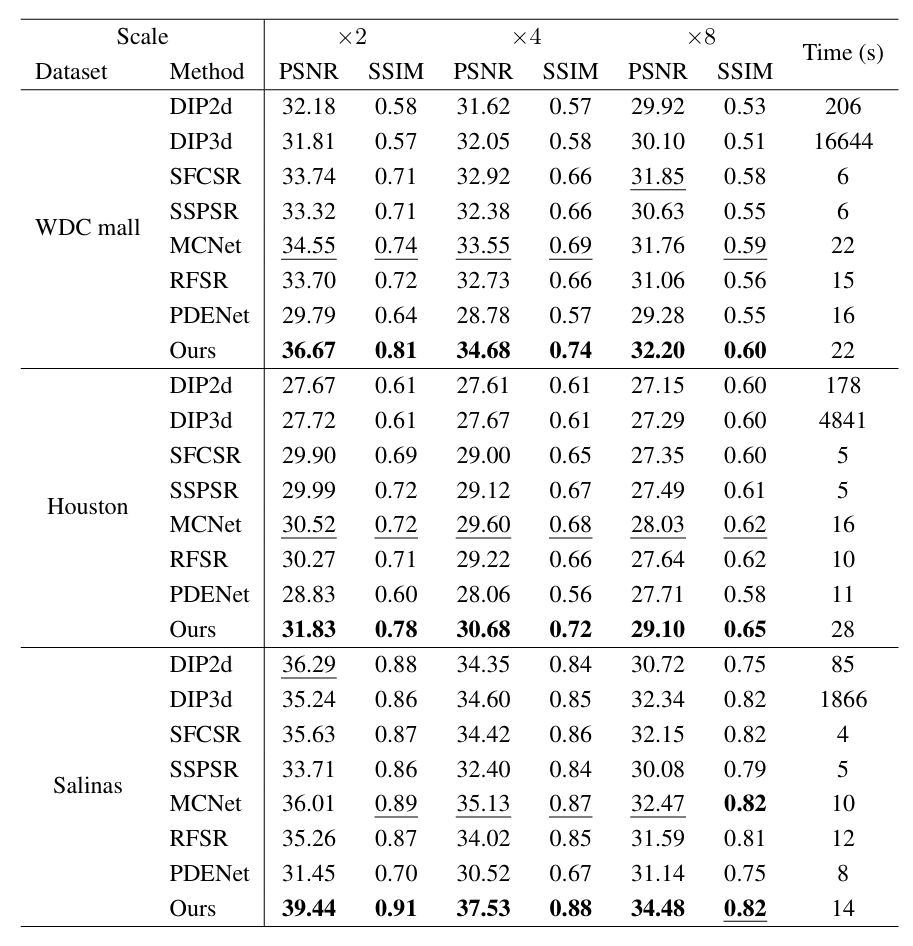
实验结果表明，HIR-Diff 在各缩放倍率下均保持较高 PSNR 和 SSIM。例如，在 Salinas 数据集 ×2 缩放下，HIR-Diff 的 PSNR 达到 39.44，SSIM 为 0.91，相比传统方法 MCNet 提升约 3 个 PSNR 单位。与此同时，HIR-Diff 在运行时间上也具有优势，例如在 WDC mall 数据集 ×4 缩放下仅需 22 秒，而 DIP3d 的运行时间超过 1600 秒。

（3）缺失像素恢复对比

对于缺失像素修复任务，实验在掩膜率 0.7、0.8、0.9 条件下进行对比，方法包括 TRPCA、TRLRF、S2NTNN、HLRTF 以及深度学习方法（DIP2d、DIP3d、DDS2M）。

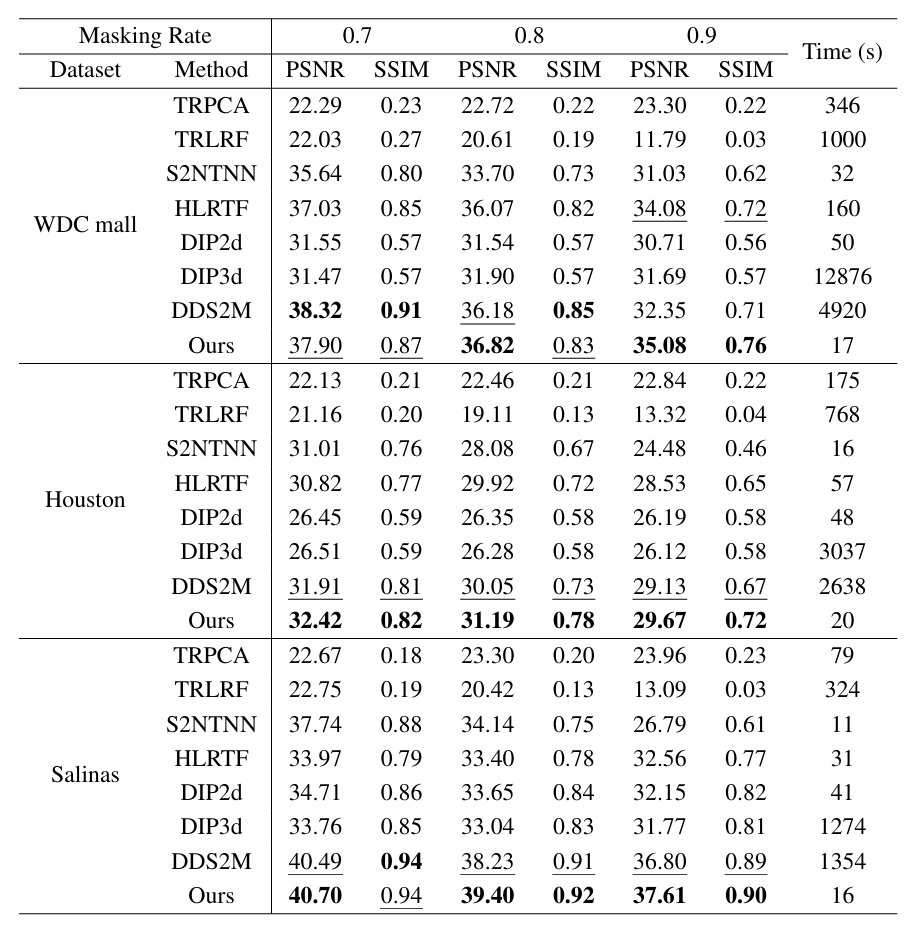
结果显示，HIR-Diff 在各掩膜率下表现稳定。例如，在 Salinas 数据集掩膜率 0.9 时，HIR-Diff 的 PSNR 和 SSIM 分别为 37.61 和 0.90，明显优于低秩方法 TRLRF。部分情况下，DDS2M 的指标可能略高，但其运行时间长达数千秒，而 HIR-Diff 仅需十几秒完成推理，体现出良好的效率优势。

3.4 消融实验

为了验证 HIR-Diff 的核心设计模块对高光谱图像恢复的作用，论文进行了系统的消融实验。实验主要考察了低秩分解策略、指导函数以及噪声调度对不同任务的影响，包括去噪、超分辨率和图像修复。

（1）低秩分解策略

作者对比了三种方式：仅使用 SVD 生成的降维图像A、通过最小二乘法求解部分波段来估计系数矩阵，以及当前多结合策略。

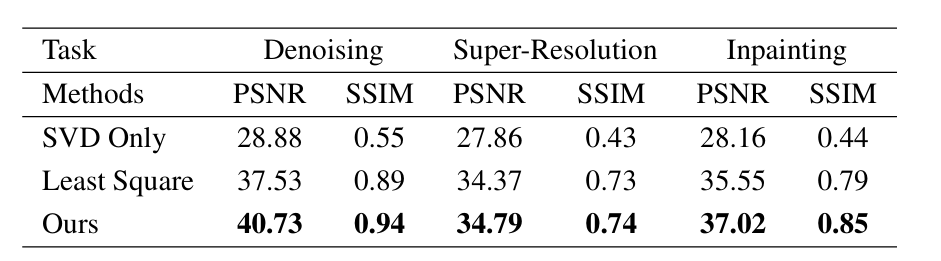
实验结果显示，原方法在各类任务中都显著优于其他两种策略。例如，在去噪任务中，采用原方法的恢复图像 PSNR 达到 40.73，而 SVD Only 的 PSNR 仅为 28.88；在图像修复任务中，SSIM 从 0.44 提升到 0.85。这表明通过合理选择波段并结合低秩分解，可以有效抑制噪声，同时让生成的低维图像更符合扩散模型的先验分布，从而提升恢复质量。

（2）RRQR策略消融

此部分重点考察了不同波段组合对恢复性能的影响。

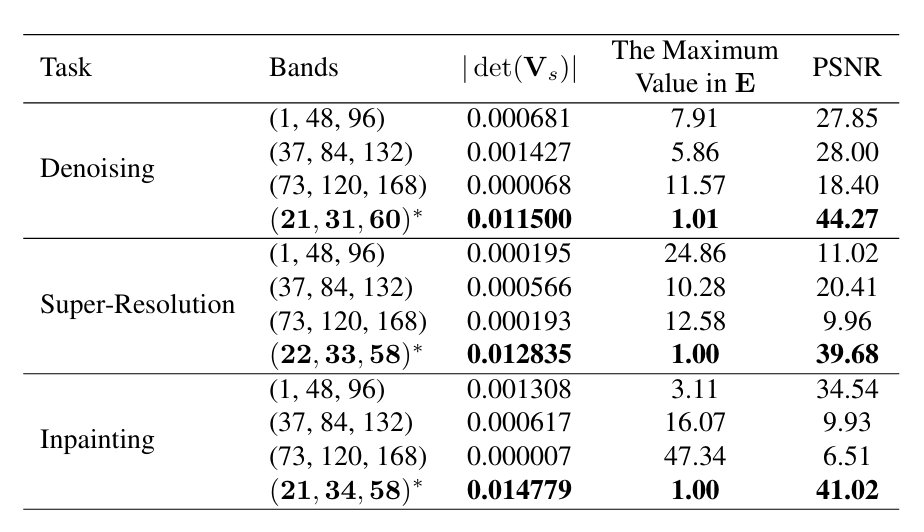
可以看到，当使用论文提出的波段选择策略时（带 * 的组合），行列式值较大且 E 的最大值接近 1，对应的 PSNR 远高于其他波段组合。例如，在去噪任务中，带 * 的组合 PSNR 达到 44.27，而等间隔选择的组合仅为 27.85 或更低。这说明 RRQR 能有效挑选出信息丰富且互相独立的波段，使系数矩阵估计稳健，从而提升恢复性能。

（3）指导函数消融

完全去掉指导函数时，模型表现非常差，PSNR 和 SSIM 均处于极低水平，仅为 10.12 和 0.07；仅保留数据保真项可以大幅提升恢复效果，去噪任务的 PSNR 提升到 34.99，SSIM 达到 0.87。而完整的指导函数组合（数据保真 + TV 正则化）进一步提高了图像的细节和结构保真度，PSNR 和 SSIM 分别达到 36.14 和 0.90。这说明指导函数不仅保证了恢复图像与观测数据的一致性，还能帮助保持图像边缘和纹理信息。

（4）指数噪声调度消融

作者对比了线性、余弦和指数三种调度策略，并在不同采样步数下观察性能变化。

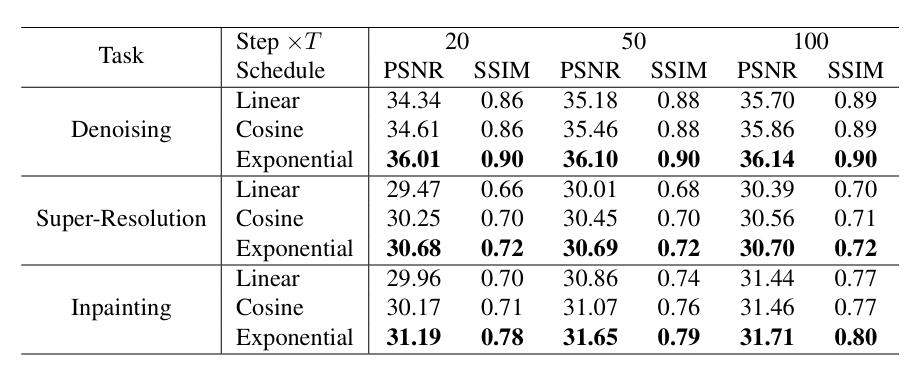
结果显示，指数噪声调度在采样步数较少时依然能够保持较高的恢复质量。例如，在去噪任务中，采样步数为 20 时，指数调度的 PSNR 达到 36.01，SSIM 为 0.90，而线性和余弦调度的 PSNR 分别仅为 34.34 和 34.61。类似趋势在超分辨率和图像修复任务中也存在。由此可见，指数调度可以在前期快速去除高强度噪声，后期缓慢下降以精修细节，从而在保证图像质量的同时显著加快采样速度。

四、总结

总结来看，HIR-Diff 提出了一个针对高光谱图像恢复的高效无监督框架，其核心在于将高光谱图像分解为降维图像 A 与光谱系数矩阵 E，通过 SVD 与 RRQR 对 E 进行稳健估计，再利用预训练扩散模型在降维空间恢复 A，同时引入条件引导与指数噪声调度优化采样过程。实验结果表明，该方法在去噪、超分辨率及缺失像素修复任务中均能取得与或优于现有最先进方法相当的恢复质量，同时显著降低计算开销，体现出其在高光谱图像恢复中的实用性、泛化能力和效率优势。整体而言，HIR-Diff 通过“低秩分解+扩散先验”的策略，有效解决了高维光谱数据处理中的维度与计算难题，为高光谱图像恢复提供了一种可行且高效的通用方案。