深度学习——回归问题
线性回归
一、什么是线性回归?
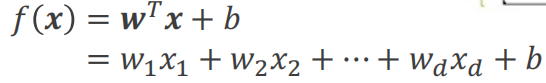
其中w是权重,b是偏移量。w和b共同称为模型参数。
损失函数L(f) = L(w,b)
线性回归的目的是找到合适的w和b使得损失函数最小。损失函数如下:
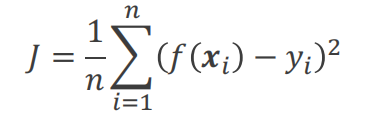
损失函数也成为Mean Squared Error (MSE)
找到损失函数后,通过损失函数找损失最小的函数f,也就是确定w和b。
梯度下降
梯度下降可以用来找最合适的w,b即确定最合适的function。
梯度下降的做法:分别对w和b求偏导。分别寻求最合适的w(b),是的损失最小。见李宏毅老师的图:
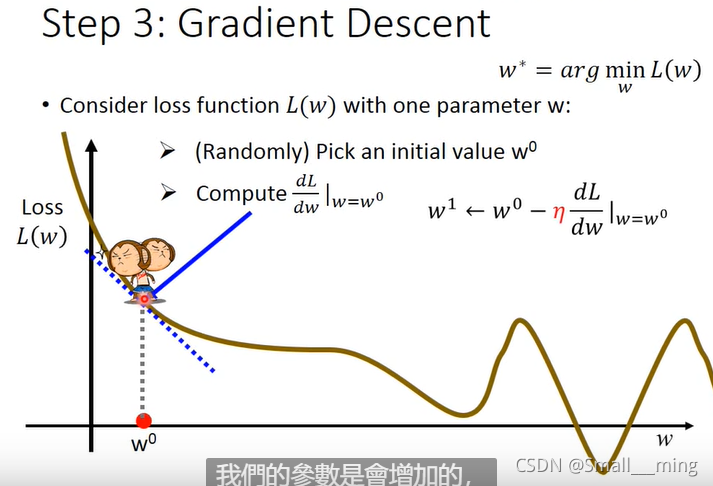
因为要找损失函数的最小值,所用要用到梯度下降。
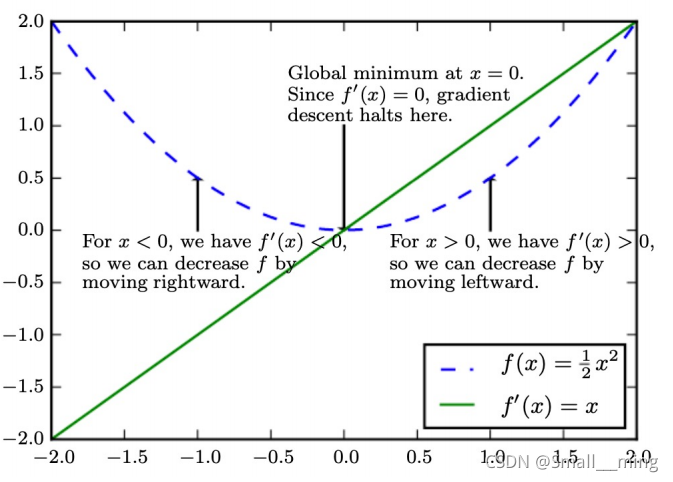
梯度下降即求函数的导数或偏导数。
由中学知识我们知道,当f’(x)<0时,f(x)递减,f’(x)>0时,f(x)递增。所以当f’(x)<0时应该向右移动,当f’(x)>0时,应该向左移动。
梯度下降就可以理解为根据f’(x)的符号来使f(x)逐渐减小。
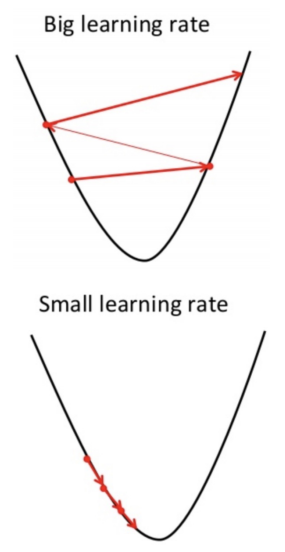
学习率
上面有提到根据梯度下降我们要移动,移动的大小即为学习率。
二、逻辑回归
线性回归的范围是(-∞,+∞),逻辑回归的范围是[0,1]。通过S型函数即可将线性回归转为逻辑回归。
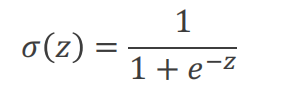
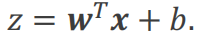
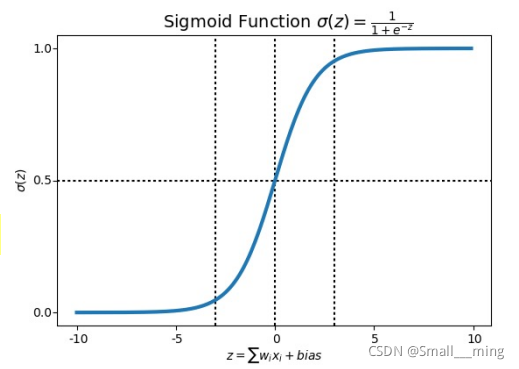
函数图像如下所示:
损失函数如下:
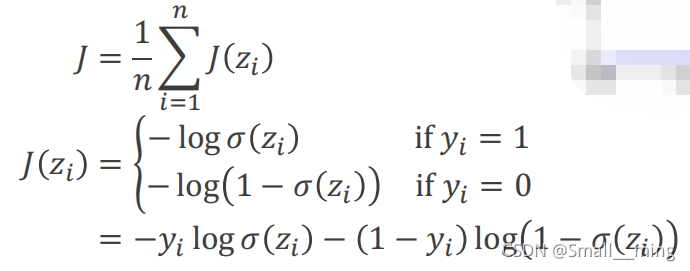





 本文介绍了深度学习中的两种基本模型:线性回归和逻辑回归。线性回归探讨了模型参数w和b的优化,通过最小化Mean Squared Error (MSE)损失函数来寻找最佳拟合。梯度下降作为优化方法被用于调整参数,学习率决定了参数更新的步长。逻辑回归则将线性回归的输出转换为[0,1]区间,适用于分类问题,其S型函数将线性预测值转化为概率。
本文介绍了深度学习中的两种基本模型:线性回归和逻辑回归。线性回归探讨了模型参数w和b的优化,通过最小化Mean Squared Error (MSE)损失函数来寻找最佳拟合。梯度下降作为优化方法被用于调整参数,学习率决定了参数更新的步长。逻辑回归则将线性回归的输出转换为[0,1]区间,适用于分类问题,其S型函数将线性预测值转化为概率。

















 1100
1100

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








