【GWO】灰狼优化算法(Grey Wolf Optimizer, GWO)理论分析与matlab性能仿真,使用CEC2017测试

目录

一、GWO灰狼优化理论简介

二、使用matlab实现GWO优化算法 

三、测试CEC2017中F1~F5，F11~F15

---

一、GWO灰狼优化理论简介

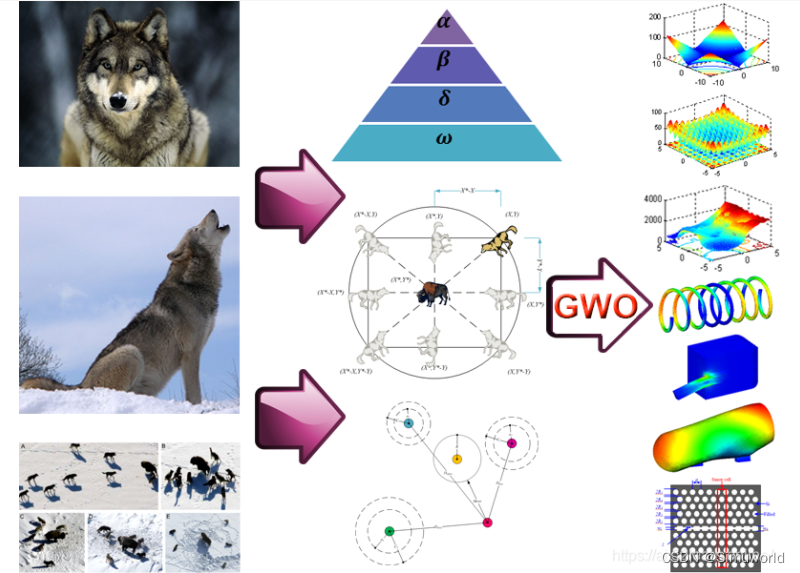
    由澳大利亚格里菲斯大学（Griffith University）研究学者 Seyedali Mirjalili 于 2014 年提出，是一种模拟自然界中灰狼的等级制度与狩猎行为的群智能优化算法，具有操作简单、调节参数少、编程易实现等特点。首先介绍了 GWO 的仿生学原理及其进化公式，然后对 GWO 的进化过程进行描述，最后给出 GWO 的伪代码与时间复杂度分析。
       α \alphaα 位于顶端，代表狼群中的头狼，负责做出狩猎，休息等决策；由于其它的狼需要服从 α \alphaα狼的命令，所以 α \alphaα狼也被称为支配狼。另外， α \alphaα 狼不一定是狼群中最强的狼，但就管理能力方面来说， α \alphaα 狼一定是最好的。
        β \betaβ是 α \alphaα 的从属者，它们的职责是协助 α \alphaα 做出决策，当已有的 α \alphaα 失去优势时，它们也是代替其成为新的 α \alphaα 的最佳候选者；在 α \alphaα狼去世或衰老后，β \betaβ 狼将成为 α \alphaα 狼的最候选者。虽然 β \betaβ 狼服从 α \alphaα 狼，但 β \betaβ 狼可支配其它社会层级上的狼。