4、手把手教你入门设计半桥LLC开关电源设计，基波近似法FHA提取基波交流信号的公式推导

基波近似法（FHA）

在LLC电路中常用基波近似法，既FHA建模方法。来对输入信号进行提取，只考虑其傅里叶级数分解中的​​基波分量​​（即频率最低、能量最大的正弦波），而忽略所有高次谐波的影响。这时原本复杂的非线性电路就可以被等效为一个线性的正弦交流电路，从而可以运用经典的交流电路理论（如欧姆定律、基尔霍夫定律）来推导系统的电压增益、输入阻抗等关键特性。

这种方法的准确性建立在工作频率接近谐振频率的前提下。当工作频率远离谐振点或负载变化很大时，由于忽略了谐波分量，分析结果会产生较大误差。因此，FHA通常用于初步设计，最终验证往往需要更精确的仿真或实验

输入信号函数定义

通常LLC变换器上下管为各占50%的导通时间在周期内交替开通（忽略死区时间），且LLC前级一般都会有PFC升压电路，此时输入电压Vin为400V，后面以400V输入的一个方波为例。

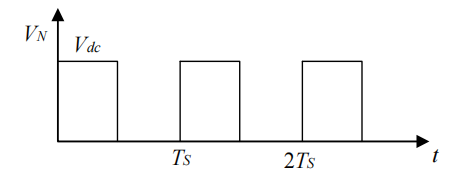
方波参数为（幅值400V，占空比50%，在0到T/2期间为400V，T/2到T期间为0V），这时函数表达式为

$$f(t)=\{\begin{array}{ll}400V& 0\le t<T/2\\ 0& T/2\le t<T\end{array}$$

傅里叶级数展开一般表达式为
$$f(t)=\frac{a_0}{2}+\sum _{n=1,2,3,4}^{\infty }[(a_n\cos (n2\pi f_{sw}t)+b_n\sin (n2\pi f_{sw}t)]$$

其中系数计算公式为
直流分量：
$$\frac{a_0}{2}=\frac{1}{T}{\int }_0^{T}f(t)dt$$

余弦项系数$a_n$:

$$a_n=\frac{2}{T}{\int }_0^{T}f(t)\times cos(2\pi f_{sw}nt)dt$$

正弦项系数$b_n$:

$$b_n=\frac{2}{T}{\int }_0^{T}f(t)\times sin(2\pi f_{sw}nt)dt$$

提取直流分量

已知直流分量是信号在一个周期内的平均值

$$\frac{a_0}{2}=\frac{1}{T}{\int }_0^{T}f(t)dt=\frac{1}{T}({\int }_0^{T/2}{V}_{in}dt+{\int }_{T/2}^{T}0dt)$$

计算积分后

$${\int }_0^{T/2}$$