无符号数和定点数的乘法运算

一、无符号乘法的硬件逻辑实现

1.基本思想

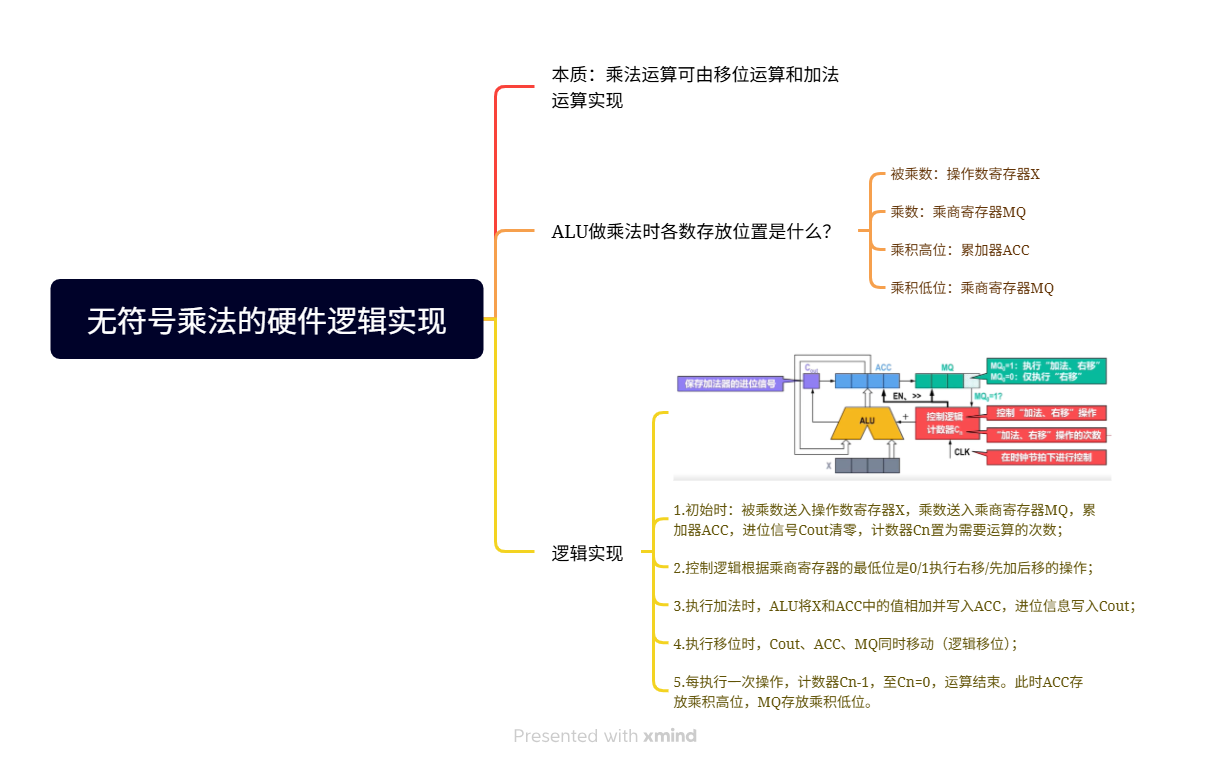
乘法运算可由移位运算和加法运算实现。

2.逻辑实现

1）初始时：被乘数送入操作数寄存器X，乘数送入乘商寄存器MQ，累加器ACC，进位信号Cout清零，计数器Cn置为需要运算的次数；

2）控制逻辑根据乘商寄存器的最低位是0/1执行右移/先加后移的操作；

3）执行加法时，ALU将X和ACC中的值相加并写入ACC，进位信息写入Cout；

4）执行移位时，Cout、ACC、MQ同时移动（逻辑移位）；

5）每执行一次操作，计数器Cn-1，至Cn=0，运算结束。此时ACC存放乘积高位，MQ存放乘积低位。

---

二、定点数原码乘法运算的硬件实现

1.本质

转化为无符号数的乘法运算。

2.运算公式

• 将数的绝对值看作无符号数乘法运算

• 符号位单独用乘数与被乘数的符号位异或得到

---

三、定点数补码乘法的硬件逻辑实现

1.补码一位乘法运算的公式

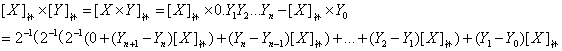
本质：补码乘法运算可通过加法和算术右移实现

2.逻辑实现

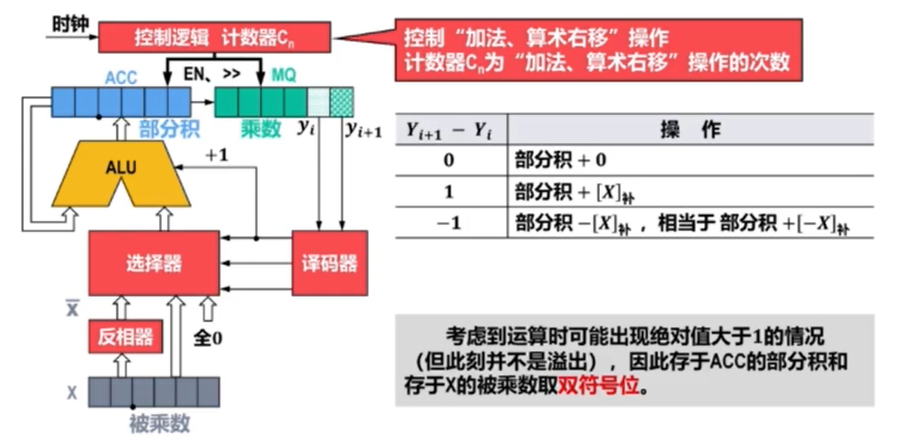
被乘数的补码乘以乘数的后一位与前一位的差再右移一位，循环直至Cn=0，最后再进行一次加法

1）需要增加一位辅助位Yi+1

• 当Yi+1-Yi=0时，部分积+0；

• 当Yi+1-Yi=1时，部分积+[X]补；

• 当Yi+1-Yi=-1时，部分积-[X]补（+[-X]的补码）

2）ACC和X采用双符号位

因为可能出现绝对值大于1，但并不是溢出的情况

3）结果需要舍弃MQ最后两位

符号位和辅助位

3.实现流程

---

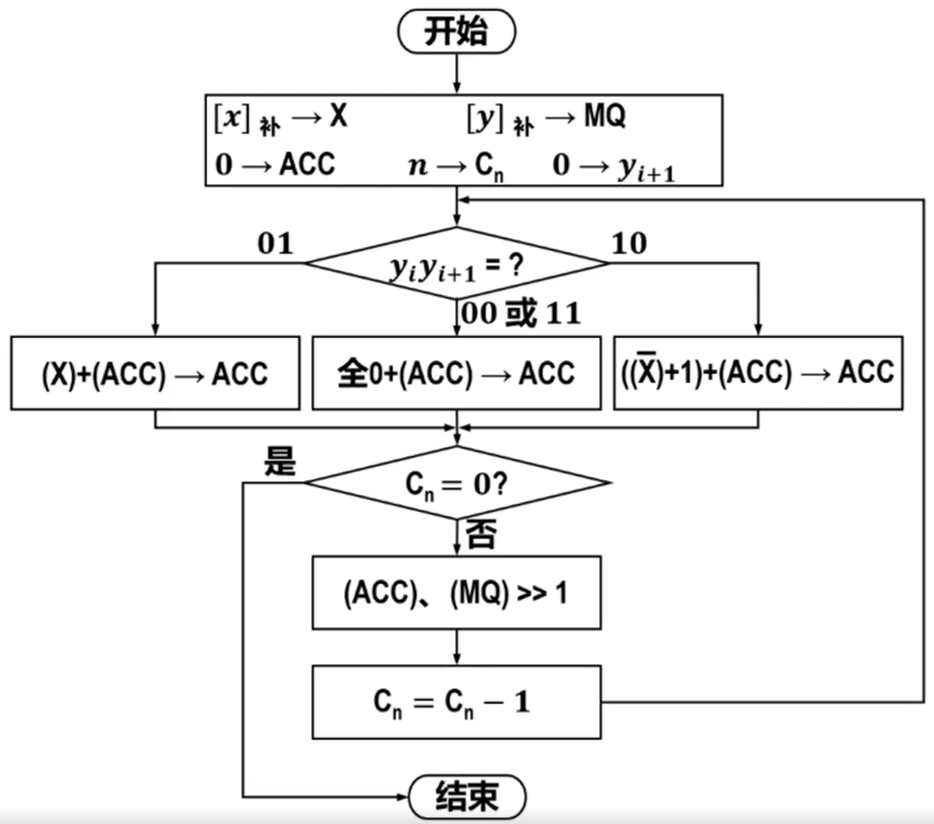
四、阵列乘法器

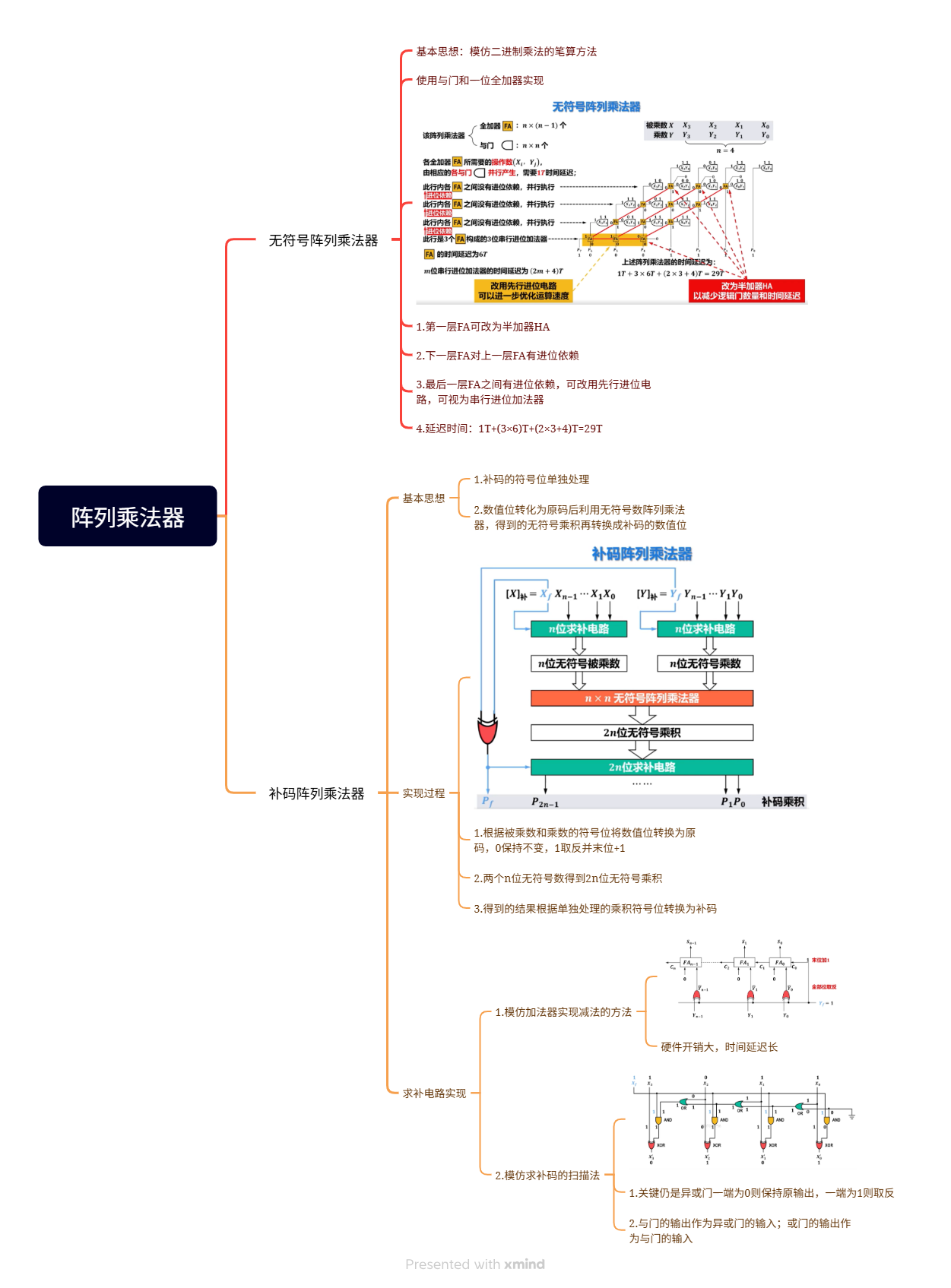
1.无符号阵列乘法器

1）基本思想

模仿二进制乘法的笔算方法。

2）逻辑实现

使用与门和一位全加器FA实现

• 第一层FA可改为半加器HA

• 下一层FA对上一层FA有进位依赖

• 最后一层FA之间有进位依赖，可改用先行进位电路，可视为串行进位加法器

• 延迟时间：1T+(3×6)T+(2×3+4)T=29T

2.补码阵列乘法器

1）基本思想

• 补码的符号位单独处理

• 数值位转化为原码后利用无符号数阵列乘法器，得到的无符号乘积再转换成补码的数值位

2）逻辑实现

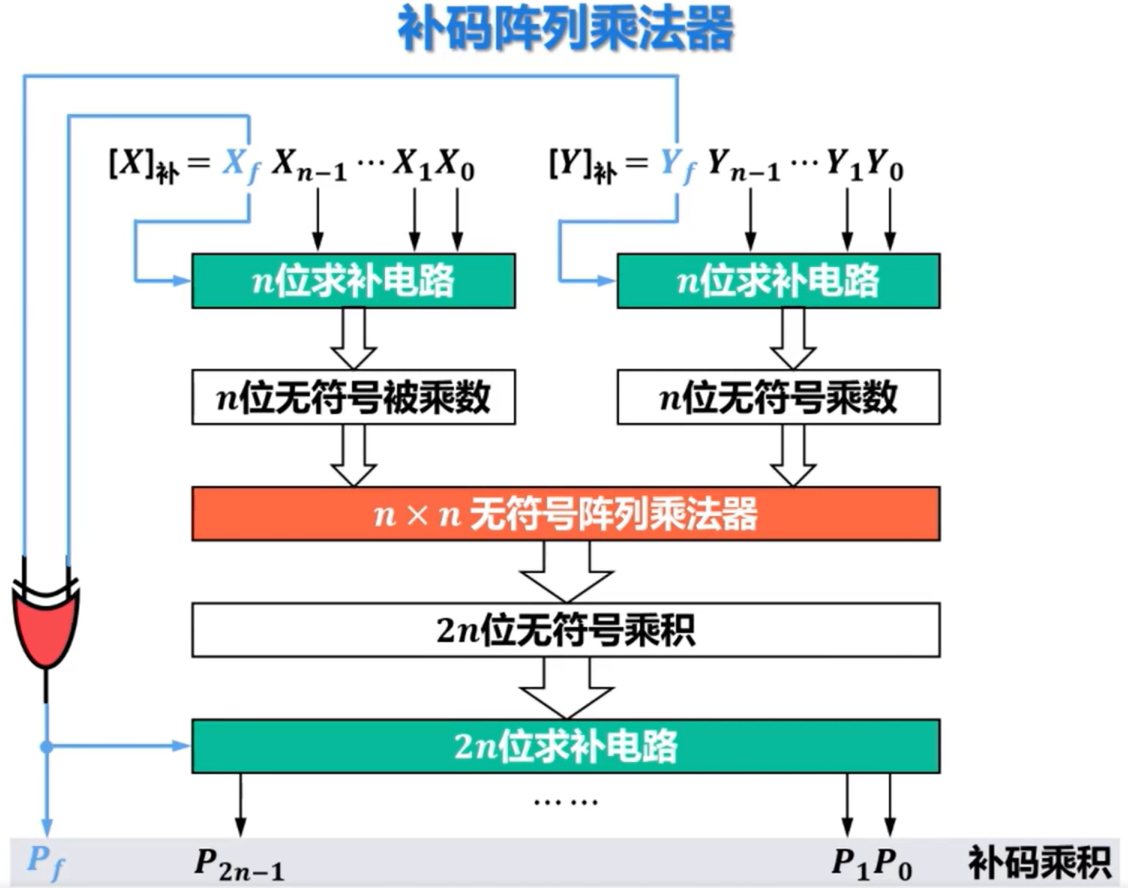
• 根据被乘数和乘数的符号位将数值位转换为原码，0保持不变，1取反并末位+1

• 两个n位无符号数得到2n位无符号乘积

• 得到的结果根据单独处理的乘积符号位转换为补码

3）求补电路实现

• 模仿加法器实现减法的方法（硬件开销大，时间延迟长）

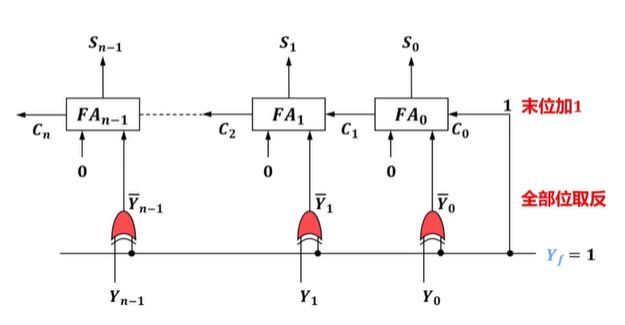
• 模仿求补码的扫描法

  
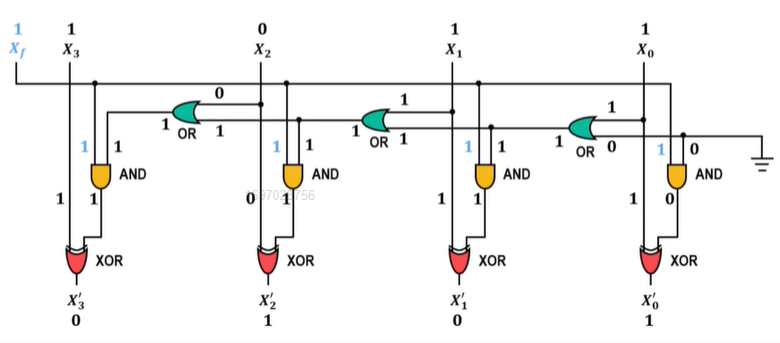
  关键仍是异或门一端为0则保持原输出，一端为1则取反；与门的输出作为异或门的输入；或门的输出作为与门的输入。