计算机组成原理－－无符号数、有符号数的乘法器

　　做而论道最近发表的几篇博文，都是关于二进制乘法器电路的。　既有无符号数乘法的电路、也有有符号数（补码）乘法的电路。　做而论道给出的电路，都是采用 “加法器阵列” 来完成乘法运算的。　对于许多《计算机组成原理》教材上津津乐道的 “相乘-移位-相加” 方法的乘法运算，做而论道并没有给出电路。　因为，这种移位式的算法，速度太慢，远远落后于时代的步伐，不值得讨论。
　　做而论道的这个想法，也并非是特立独行。　在白中英主编的《计算机组成原理》中，也有同样的阐述，摘录一段如下：
　　在早期计算机中为了简化硬件结构，采用串行的 1 位乘法方案，即多次执行 “加法-移位” 操作来实现。（这种乘法器称为：串行乘法器）。这种方法并不需要很多器件，然而串行方法毕竟太慢，不能满足科学技术对高速乘法所提出的要求。
　　... ...
　　自从大规模集成电路问世以来，高速的单元阵列乘法器应运而生。　出现了各种形式的流水式阵列乘法器，它们属于并行乘法器。　鉴于串行乘法器已被淘汰，下面只介绍并行乘法器。
　　正是因为这个理由，在白中英主编的《计算机组成原理》中，就没有介绍采用 “相乘-移位-相加” 这种低速运行的乘法器。　而是直接就介绍了采用 “加法器阵列” 构成的乘法器。　该书上的逻辑电路图如下。

　　（本图摘自网上，可见：定点数的乘法运算，侵删。）
　　白老师介绍的全加器阵列乘法器，虽然仅仅是给出了 “逻辑电路图”，远远不如做而论道介绍的实际电路更为深入，尽管如此，也还是走向了正确的方向。　而在许多教材上谆谆教导的 “布斯法、原码补码二位乘”，都是早就属于淘汰之列，用不着深究了。　这些，还在用于考研吗？　还是算了吧。

　　上述乘法器 “逻辑电路图”，是用于 “不带符号数”（即无符号数）相乘的，当然就不能进行 “有符号数” 的乘法运算了。　为此，白老师又给出了一个 “对 2 求补器” 的电路，可将 “补码转换成原码”，同时，该电路也能把 “原码转换成补码”。
　　先后两次应用 “对 2 求补器” 电路，即可将补码转成无符号数，以无符号数相乘之后，再转成补码进行保存。　这就能实现 “有符号数” 的乘法运算了。　实现这个思路的框图如下。

　　按说，白老师的想法是正确的。　但是，实现的方法，却是既啰嗦、又过于简单了。　“求补器” 的电路，就已经是相当复杂了。　在“无符号数” 的乘法器的前后，安装上这三套求补器，不但整个电路的规模不可忽视，而且，安上之后，它也不能简单的移除。　因为白老师并没有给出移除的方法。　因此，按照这个方法加以改造，虽然能够实现 “有符号数” 的乘法运算，但是，却难以恢复为原来的 “无符号数” 乘法运算功能。　顾了这头，忘了那头，考虑的，略微有点不周啊！

　　对与这个问题，做而论道，不但早就有了更简单方便的方法，而且，也已经设计成功了完美的 “通用乘法器” 电路。　下面逐步进行介绍。　　　

---

　　先看一个 “无符号数” 相乘的计算方法吧。

　　乘法的竖式，大家都懂的。　虽然多了几个 0，也不足为奇。　下面，就是完成这个 “无符号数” 乘法运算的电路图。

　　图中，用拨动开关输入的两个乘数，分别是：A = 1101、B = 1011。
　　经过本电路进行 “无符号数” 乘法运算，在图中输出了乘积：1000 1111。　计算完全正确。
　　图中，四个与门一组，共有四组。　每一组，都是用于完成：Bi × A 的操作。
　　图中，有三个加法器芯片（75LS283），它们是完成四项部份积（Bi × A）相加的工作。
　　观察各个加法器输入引脚的连线，可看到：各项部份积之间有明显的 “错位”。　按照这种“错位” 的连线方法，就完成了部份积的移位工作。　因此，就不要再讨论什么 “数据移位” 的操作了。　按照这种连线方法，整个乘法器，就是以 “芯片级” 的速度工作了。　这就要比 “来一个脉冲移动一位”，快上百倍千倍甚至上万倍。

---

　　看懂了 “无符号数” 乘法的方法和电路，就可以讨论一下 “有符号数” 的乘法运算了。
　　下面是 “有符号数” 相乘的计算方法。

　　图中 “有符号数” 相乘的计算方法，使用的是：补码一位乘（校正法）。
　　与 “无符号数” 的乘法比较，差异，还不算太大吧？　哦，有两个地方不同。
　　首先，符号位需要扩充，在原有符号位的基础上，至少要增加一位（可见图中的几个 1）。
　　第二，由于补码的最高位（即 B3）是一个负数，所以，最后一项部份积，与前面几项相比，就是一个 “负数”。　针对该项，应该采用 “减法运算”，这就是所谓的 “校正”。

　　原先，四位无符号数，乘以，四位无符号数，使用四位的加法器，就够用了。　现在为了进行补码运算，就多了一个符号位的事，加法器，就必须增加一位数。（这就是用补码运算的缺点之一。）　做实验时，增加一位，不现实。　为了增加一位，就只能再增加一块加法器芯片（74LS283）。
　　为了在最后一项的实现减法运算（即所谓的校正），可以采用以前讲过的 “取反加一” 电路。　乘数 A 有四位数，那么，就用四个异或门，再由 B3 进行控制，即可。

　　用补码一位乘（校正法）完成 “有符号数” 乘法运算的电路如下所示。

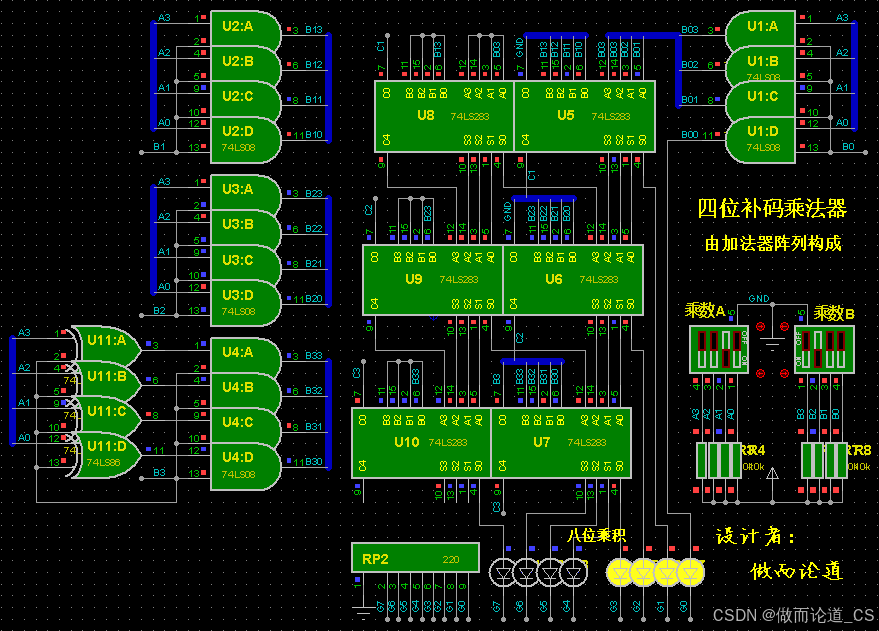
　　由图可见，使用了两片加法器芯片，扩充了运算位数，满足了增加符号位的位数需求。　　
　　在图中左下部，增加了四个异或门，由 B3 进行控制。
　　当 B3 为 1 时，异或门就会输出 A 的非，即为对 A 取反。　同时 B3 的这个 1，又加到了 U7 的进位输入端。　于是，A 就被 “取反加一” 了。　乘数 A，就以－A 的形式进入了加法器，这就实现了－A 的运算。　（采用异或门，实现取反加一，即可完成减法运算。　这个原理，可在做而论道以前的博文中找到。）
　　当 B3 为 0 时，异或门后面的四个与门和 B3 相与，与门的输出，就是 0 了。

　　在图中，输入的补码是：A = 1101、B = 1011。
　　本电路，输出的补码是：0000 1111。
　　这些补码，对应的数值运算，则是：(－3 ) × (－5 ) = +15。　运算正确。

　　感兴趣的网友，可以利用 PROTEUS 软件，仿照上面两个电路图，自己绘出电路，并进行仿真测试，你可随便输入任何值，即可测试出：做而论道给出的电路，输出，都是正确无误的。

　　把上面两个电路，结合起来，就可以构成一个：通用的乘法器。
　　写了不少了。　这个通用的电路，还是，下次再说吧。

－－本文完－－