定点数和浮点数_定点数运算

什么是定点数？定点数应用的场景有哪些？定点数怎么进行四则运算？

首先来看一下什么是定点数，定点数和浮点数是个相对的概念，定点数，即带一个固定小数点的数，小数点的位置固定，例如怎么用一个16bit整数来表示一个带5位小数的数呢？

上图是我们常见的整数的位存储，此时小数点位在bit0的右侧，如果我们将小数位移动到bit5的右侧，是不是可以实现带5位小数的数呢？如下图所示，我们可以通过定义一个小数点的位置，来表示一个带指定位小数的数。

为什么要使用定点数？

对于大部分低档次的微处理器，都是不支持硬件浮点数运算的。一般软件在处理浮点数运算时，会占用更多的ROM和RAM空间，因此浮点数的运算会比整数运算需要更多的时间，对于一个8位的微处理器来讲，进行浮点数加法运算可能需要几百微秒，而进行16位的整数运算只需要几微秒的时间，在进行浮点数乘法和除法运算时，需要的时间会更长，如何尽量少的避免浮点数运算呢？我们可以将浮点数转换成定点数，然后来进行加减乘除四则运算。定点数的运算是整数的运算，主要的目的是使计算机认为我们在进行整数的运算，而实际上我们是在运算带有小数的数。

定点数如何表示？

这里我们定义一个式子来表示定点数：

定点数尾数指数

其中S表示尾数需要按照比例缩小2^指数倍来决定该定点数的值，通过这种记法来与浮点数区分:

浮点数尾数指数

下面是一些定点数表示的例子:

表示或表示或

尾数是根据需要来选择用一个变量中的多少bit用来给尾数的，而指数也是根据具体的精度来设置小数点的位置的。

如何将一个浮点数转换为一个定点数？

• 正数(0.0 < x ≤ 65535.0)

其中INT()是用于对结果取整，因为定点数本身就是整数，当x为0.0时，尾数和指数都是0，下面来举一个实际的例子，将1.2345转换成定点数的表达形式:

• 正数(x > 65535.0)

照样举一个例子，将107573表示为定点数：

• 有符号数(-32767.0 ≤ x ≤ +32767.0，0.0除外)

• 有符号数(x < -32767 或  x > +32767)

定点数的四则运算

• 定点数的加减法

对于两个定点数的加法和减法，两个定点数的指数必须是一样的，例如将20480S -15(0,6250) 与 31745 S -18(0.1211)相加，首先需要将小的数转换成大的数字相同的数量级，然后尾数除以8：

即为3968 S-15，然后将两个值进行加法，得到：

但是在加法时需要注意结果是否溢出，需要注意有符号和无符号的定点数最大值，下面来举一个例子：

假设该数是有符号的16位定点数，那么加完之后的结果就显然溢出了，我们知道有符号的16位数范围：-32768~32767，所以此时就必须小心(对应在代码里面需要加溢出检查)，遇到这种情况我们的处理方法如下：

• 定点数的乘法

定点数乘法原则，只需要将两个数的尾数进行相乘作为结果的尾数，指数相加即可，下面还是来举一个两个有符号的16位定点数相乘的例子：

相乘的结果会得到一个32位的结果，当然也可以将32位的结果转换成16位的结果，将尾数右移15位(32768)，得到的结果将是19671 S-18

再来举一个两个无符号的16位定点数相乘的例子：

当然也可以将该32位的结果转换为16位的，除以65536(右移16位)得到39681 S-19

• 定点数的除法

在进行定点除法时，可以简单地除以尾数并减去指数或者将除法转换成乘法，比如：

根据上面的公式可以转换为：

但是此时转换成定点数来计算的结果是不正确的，因为在进行定点运算的时候产生了一个余数8235，此时编译器是不对此余数进行处理的，所以导致了计算结果非上面一个算式的结果，此种情况怎么处理呢？我们可以适当地将被除数"扩大一定倍数"，可以得到下面的一个式子：

上式中乘以了一个32768 S-15，其实系数就是1，只是前面的尾数扩大了一定的倍数，但是实际的值并没有变，然后还要注意，如果此时定义的结果是一个有符号的16位，那么此时计算结果的尾数还需要调整，应作如下调整：

当计算结果的尾数大于分母的尾数时，就会发生溢出，因此需要在进行代码设计时，必须检查溢出。

• 定点数比较

两个定点数在进行比较时：两个数的指数必须相同。一旦两个数表示成了相同的数量级，对比这两个数就是一件简单的事情，只需要比较尾数即可。

定点数运算的几个实例

计算圆的周长

假设直径范围从1.22到20.8英寸，直径为一个正数，可以使用无符号16位定点数类型来定义，圆周率可以用以下定点数来表示：

假设需要一个5位整数(可表示0-31英寸)来表示圆的直径，其他11位用来保存小数，直径的定点数可以表示为：

尾数

C语言代码实现：

type.h:

typedef signed short INT16S;
typedef unsigned short INT16U;
typedef signed int INT32S;
typedef unsigned int INT32U;

#include 

INT16U Circumference(INT16U diameter){
    INT16U x;
    
    x = (INT16U)((51472L * (INT32U)diameter) >> 16);
    return (x);
}

假设我们代入一个1.22英寸的直径进行计算，根据对直径的要求，有11位小数位，那么

最终计算的结果为1961 S-9(3.830078)，更为精确的结果为3.832743，误差在0.07%以内。

计算圆柱的体积

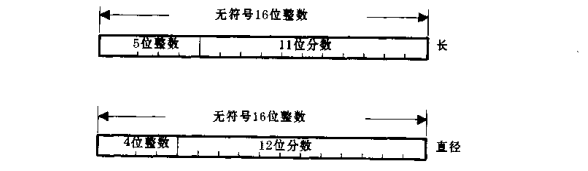
假设圆柱的高h的范围为9英寸到24英寸，直径d从1英寸到12英寸，为了计算圆柱的体积，因为变量都是正数，所以将都使用无符号的整数来进行计算。圆柱的高h使用一个无符号16位整数来表示，其中5位来表示整数部分，其余11位表示小数部分，圆柱的直径d也是使用无符号16位整数来表示，其中4位用于表示整数，其余12位用于表示小数部分。

尾数尾数

C语言代码的实现：

#include 

INT16U Volume(INT16U length, INT16U diameter){
    INT32U x;
    INT32U dia;
    
    dia = (INT32U)diameter;       // S - 10 Result
    x   = (51472L * dia) >> 16;       // S - 6 Result
    x   = (x * dia) >> 16;     // S - 1 Result
    x   = (x * (INT32U)length) >> 16; // S - 3 Result
    
    return ((INT16U)x);
}

假设代入一个高为9英寸、直径为1英寸进行计算，高h和直径d可以分别用定点数来表示：

返回值的结果还需要按比例缩小S-3，得到的结果为56 S-3(7.00)，较为精确的结果为7.06858，计算结果的误差为0.98%

开华氏温度的转换

开氏温度℃转化为华氏温度℉，公式如下：

℃℉

在利用定点数运算来实现此转换公式时，需要知道将要处理的温度范围，假设温度范围为-40℉-250℉，根据这个温度范围需要选择变量的类型，为有符号16位整数，需要8位来表示整数，7位来表示小数位，1位表示符号位，其中32℉表示4096 S-7，常数5/9可以表示为18240 S-15。

C语言代码实现：

#include 

INT16S FtoC(INT16S f){
    return (((INT32S)(f - 4096) * 18240) >> 15);
}

华氏温度℉转化为开氏温度℃，公式如下：

℉℃

其中常数9/5可以表示为29491 S-14。

C语言代码实现：

INT16S CtoF(INT16S c){
    INT16S x;
    
    x = ((INT32S)c * 29491) >> 14;
    return (x + 4096);              //Result is S - 7
}

总结

在进行定点数运算时，前提条件需要知道变量的取值范围。定点数运算操作通常在执行时是快速的，因为大部分MCU在执行整数操作时性能是非常好的。性能是以精度和复杂性为代价的，为了提高精度就不得不使用更多的位。当使用小的数进行定点数运算的产生的误差较大，而使用较大数进行运算时会得到较好的结果。