掌握这四个要素，轻松理解几乎所有机器学习算法！

什么是损失函数、优化、模型或算法？机器学习算法及其术语的深奥，往往让初学者望而生畏。

本文将通过拆解数据集、损失函数、优化方法和模型这几个要素，总结机器学习算法的每个“通用要素”。

掌握这些“要素”后，你无需再将每个新遇到的机器学习算法视为孤立的实体，而是可以将其视为以下四个常见元素的独特组合。

机器学习算法种类繁多，本文将以线性回归算法为例，来探讨这四个要素。

章中所有的数据和资料，可添加小助手无偿分享~
扫码添加小助手即可无偿获取~

也可以关注“AI技术星球”公众号，关注后回复“221C”获取。

1. 数据集的指定

机器学习模型的第一个要素是数据集。

机器学习作为应用统计学的一种，依赖于大量数据。因此，你选择的数据特征（即作为输入的重要数据）会显著影响算法的性能。

选择数据特征的艺术如此重要，以至于它有了一个专门的术语：特征工程。更多关于特征工程的内容，请参见下文。

常见示例

• X和y（输入和预期输出）→ 监督学习

• X（仅输入）→ 无监督学习

简单线性回归算法的数据集可能如下所示：

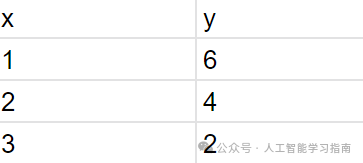
图1.0：简单线性回归数据集
 

在线性回归示例中，我们指定的数据集就是我们的X值（输入）和y值（预测值，即观测数据）。

2. 模型

模型可以看作是一个主要函数，它接受你的X（输入）并返回你的ŷ（预测输出）。

虽然你的模型可能并不总是传统数学意义上的函数，但将模型视为函数是非常直观的，因为给定一些输入，模型会对输入进行处理以执行任务（T）。

常见示例

• 多层感知机（基本神经网络）

• 决策树

• K-均值（聚类）

在简单线性回归的上下文中，模型是：

y = mx + b

其中，y是预测输出，x是输入，m和b是模型参数。

每个模型都有参数，这些参数有助于定义一个独特的模型，并且它们的值是通过从数据中学习来估计的。

例如，如果我们有第1节中的简单数据集，

图1.0（复现）：简单线性回归数据集
 

那么在线性模型中，我们的最优m和b将分别是-2和8，从而得到拟合模型y = -2x + 8。

特定的值-2和8使我们的线性模型对这个数据集来说是独一无二的。

由于我们的数据集相对简单，因此很容易确定使模型误差最小的参数值（在这种情况下，“预测”值等于“实际”值）。

以下面这个数据集为例：

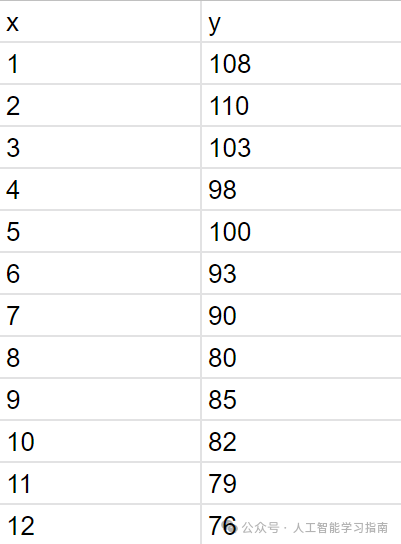
图2.0：线性回归数据集
 

图2.0的图表如下所示

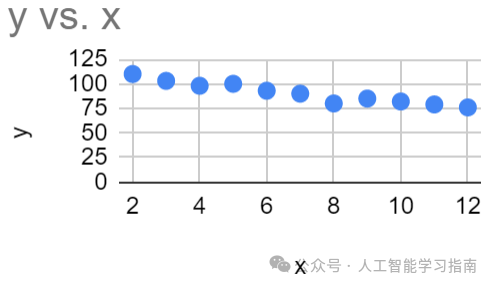
图2.1：图2.0中数据集的图形展示
 

注意，此时找到最优的m和b不再像之前的示例那样简单。

在这种情况下，我们需要通过优化损失函数来估计最适合数据的模型参数m和b。

另外我们精心打磨了一套基于数据与模型方法的AI科研入门学习方案（已经迭代第6次），对于人工智能来说，任何专业，要处理的都只是实验数据，所以我们根据实验数据将课程分为了三种方向的针对性课程，包含时序、影像、AI＋实验室，我们会根据你的数据类型来帮助你选择合适的实验室，根据规划好的路线学习 只需3-5个月左右（很多同学通过学习已经发表了 sci 一区及以下、和同等级别的会议论文）学习形式为直播＋录播，多位老师为你的论文保驾护航。

适合人群：

• 导师放养，自学无头绪

• 时间紧任务重有延毕风险

• 想提前完成大小论文为之后读博或工作做准备的

• 想通过发表sci论文、提升科研能力bao研、考研的本科同学

章中所有的数据和资料，可添加小助手无偿分享~
扫码添加小助手即可无偿获取~

也可以关注“AI技术星球”公众号，关注后回复“221C”获取。

3. 损失函数

什么是损失函数？

第三个通用要素是损失函数，通常记作J(Θ)。

机器学习算法必须有一个损失函数，当这个函数被优化时，算法的预测能够尽可能准确地估计实际值，损失函数的优化过程就是学习的过程。

在最基本的意义上，损失函数是衡量观测值/实际值与基于模型的预测值之间差异的函数。

这非常直观，如果我们的函数衡量的是观测值和预测值之间的某种距离，那么当这个距离被最小化时，随着模型的学习，观测值和预测值之间的差异将逐渐减小，这意味着我们的算法预测正在成为对实际值的更好估计。

并非所有损失函数都能轻松计算，不过我们可以使用迭代数值优化（见优化方法）来优化它。

每种任务（T）都有常见的损失函数。

常见示例

• 二次损失函数（分类、回归）*实践中不常用，但非常适合理解概念

• 交叉熵损失函数，又称负对数似然（更多关于负对数似然和最大似然估计的信息，请参见下文链接）

• 数据点与质心之间的残差平方和（K-均值聚类）

• Dice损失（分割）

在我们的线性回归示例中，损失函数可以是均方误差：

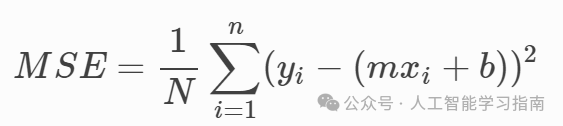
图3.0：线性回归的均方误差
 

这个损失函数衡量的是实际数据（yi）与模型预测值（mxi + b）之间的差异。

我们对这个差异进行平方，并通过除以数据点数量来对数据集取平均值。    

现在，我们可以使用优化方法来找到使损失最小的m和b。

4. 优化方法

最后是优化方法，即用于最小化或最大化相对于模型参数的损失函数的方法。

通过这个优化过程，我们正在估计使模型性能更好的参数。

优化方法主要有两种形式：

闭式优化

如果可以通过有限数量的“运算”找到函数的确切最小值（或最大值），则该函数可以进行闭式优化。

一个非常简单的例子只需要高中微积分知识。

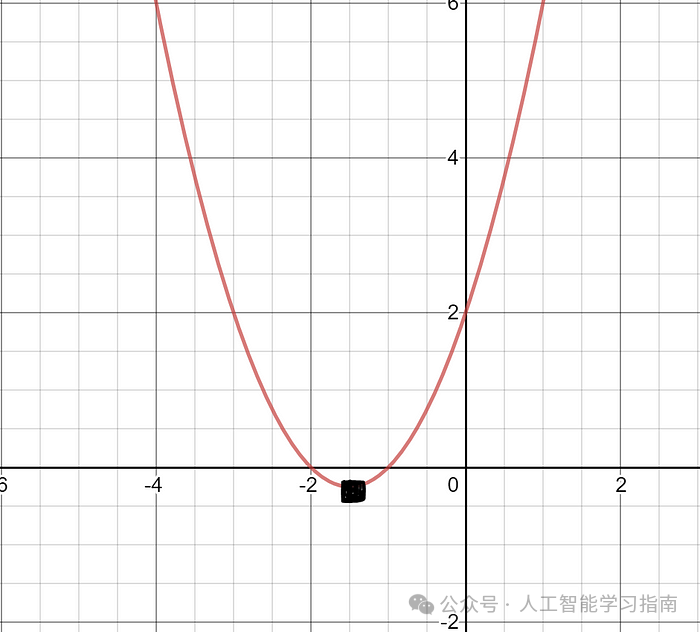
图4.0：函数J(w) = w² + 3w + 2的图形

通过对f(w)求导，并令其等于0（这是一系列有限运算），我们可以找到这个函数相对于w的确切最小值。

2w + 3 = 0 → w = -3/2

f(-3/2) = -1/4

迭代数值优化

迭代数值优化是一种估计最优值的技术。

它是最常见的优化方法，因为它通常比闭式优化方法具有更低的计算成本。

出于这个原因，许多算法会牺牲100%的准确性，以换取更快、更高效的极值估计，而且很多损失函数没有闭式解！

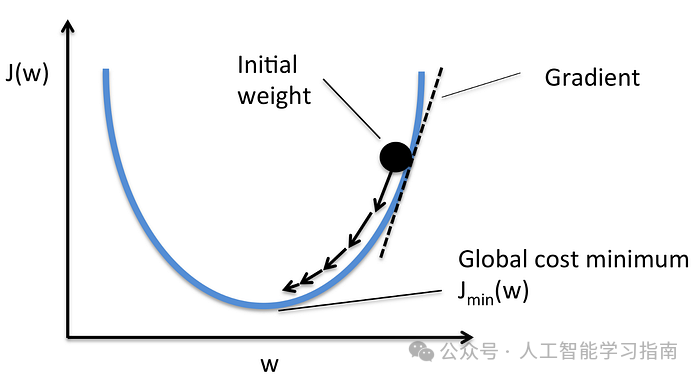
图4.1：通过随机梯度下降（SGD）寻找使J(w)最小的w值

使用闭式优化中的相同示例，我们可以想象正在尝试优化函数J(w) = w² + 3w + 2。

我们可以想象在这个图上随机选择一个点（模型参数是随机初始化的，因此初始“预测”是随机的，函数的初始值也是随机的）。

在这种情况下，我们可以使用随机梯度下降（SGD）。

最好将这种类型的迭代优化想象为一个球在山坡/山谷中滚动，如图上图所示。

常见示例

• 随机梯度下降（SGD）→ 迭代数值优化

• Adam（自适应矩估计）→ 迭代数值优化

根据《深度学习》一书，“其他算法（如决策树和K-均值）需要特殊情况的优化器，因为它们的损失函数具有平坦区域……这些区域不适合基于梯度的优化器进行最小化。”

在我们的线性回归示例中，我们可以将SGD应用于均方误差损失函数，以找到最优的m和b。

我们的算法将计算均方误差相对于m和b的梯度，并迭代更新m和b，直到模型性能收敛或达到我们选择的阈值。

这类似于图中所示的J(w)函数的导数，并使w向导数的相反方向移动，使我们更接近最小值。（斜率为正时，w变得更负）

关于反向传播的说明

许多人在深度学习的上下文中听说过反向传播这一术语。

一个常见的误解是，反向传播本身使模型学习，事实并非如此，反向传播不是优化方法。

那么反向传播在图中处于什么位置呢？

反向传播用于随机梯度下降的优化过程中的一个步骤。更准确地说，它是用于估计损失函数相对于模型参数的梯度的技术。

另外我们精心打磨了一套基于数据与模型方法的AI科研入门学习方案（已经迭代第6次），对于人工智能来说，任何专业，要处理的都只是实验数据，所以我们根据实验数据将课程分为了三种方向的针对性课程，包含时序、影像、AI＋实验室，我们会根据你的数据类型来帮助你选择合适的实验室，根据规划好的路线学习 只需3-5个月左右（很多同学通过学习已经发表了 sci 一区及以下、和同等级别的会议论文）学习形式为直播＋录播，多位老师为你的论文保驾护航。

适合人群：

• 导师放养，自学无头绪

• 时间紧任务重有延毕风险

• 想提前完成大小论文为之后读博或工作做准备的

• 想通过发表sci论文、提升科研能力bao研、考研的本科同学

章中所有的数据和资料，可添加小助手无偿分享~
扫码添加小助手即可无偿获取~

也可以关注“AI技术星球”公众号，关注后回复“221C”获取。