[2018.03.13 T2] 过河(river)

暂无链接

过河(river)

【题目描述】

在你面前有 n 条河，这 n 条河一条接着一条，并且相邻两条河之间的距离可以忽略不计。 这些河都是从南往北流的。现在你站在最西边的河边，你想要游到最东边。第 i 条河的流速 为 vi，宽 w[i] m。你游泳的速度是 u (m/s)。现在你一共有 t 秒的时间游泳。请问你最远能游到距离出发点多远的地方？注意你一定要游过所有的河。

【输入】

第一行三个整数 n,u,t 表示河的数量，游泳的速度和时间。

接下来 n 行，每行两个整数 w[i], v[i]表示河的宽度和流速。

【输出】

如果游不过所有的河，输出-1。

否则输出两行。

第一行表示你能游到离出发点多远的地方。

第二行 n 个数，表示每条河你游的时间，各个数之间用一个空格隔开。

所有输出要求保留三位小数。

【输入样例】

2 1 6
1 1
2 1

【输出样例】

11.591
2.000 4.000

【提示】

【数据规模】

对于 10%的数据，n≤1；

对于 30%的数据，n≤2；

对于 40%的数据，n≤3；

对于 50%的数据，n≤5；

对于 100%的数据，n≤50, 1≤u,t,w[i],v[i]≤1000。

题解

当时靠着贪心和物理得了15分。。。只得了两个一条河的分，再加一个-1，总共20个点，A掉3个，比期望得分低5分（没想到有20个点，以为一个一条河，一个-1，期望得分20。。。）。

本以为是一道神奇的dp，然而大佬告诉我是数学+物理orz。。。

首先，我们考虑能否游过，根据博主高一的物理知识，可以得到垂直于河岸游是最快的，我们只需要计算整个宽度除以速度得出的值，判定是否大于给定时间就可以得知能否游过了。

根据题意，我们要求出最远距离，而在保证能游到对岸的前提下，我们显然还有多余的时间，那么我们要利用这些时间在y轴方向尽可能的游远一点。因为河是从南向北流的，肯定在游的时候略向北偏更优，我们可以推导某条河中y轴方向的位移与在这条河中游的时间的函数关系如下：

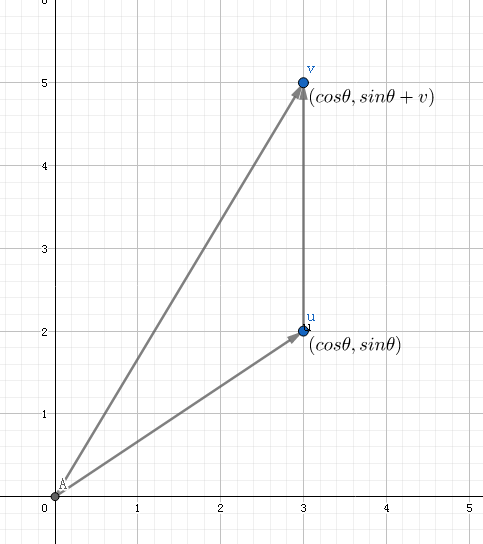
如图，设u为人的速度，v为河流速度，w为河流宽度，那么两者的和速度可表示为$(cos\theta,sin\theta+v)$，那么合速度在y轴方向上的分速度为$sin\theta+v$,那么y轴方向上的位移$F(t)$就可表示为$tsin\theta+vt$。此外，因为我们刚好花费了$t$时间，所以在x轴上又有关系$utcos\theta=w$。

我们考虑用t替换$\theta$的三角函数：

$cos\theta=\frac{w}{ut}$
$sin\theta=1-cos^{2}\theta$  

可以解得：
$$sin\theta=\frac{\sqrt{u^{2}t^{2}-w^{2}}}{ut}$$
我们把 $sin\theta$代入 $tsin\theta+vt$中，可得：
$$F(t)=\sqrt{u^{2}t^{2}-w^{2}}+vt$$
我们考虑求这个函数的导函数，设 $f(x)=x^{\frac{1}{2}}$， $g(t)=u^{2}t^{2}-w^{2}$， $h(t)=vt$：

$F(x)=f(g(x))+h(x)$
$(f(g(x)))'=f'(g(x))g'(x)$    
$f'(x)=\frac{1}{2}x^{-\frac{1}{2}}$    
$g'(t)=2u^{2}t$
$h'(t)=v$

通过上述等式，我们可以解出F(x)的导函数：
$$F'(t)=\frac{u^{2}t}{\sqrt{u^{2}t^{2}-w^{2}}}+v$$  
去掉某些无关紧要的系数，t的系数可大概化为这个形式：  
$$\sqrt{u^{2}\frac{w^{2}}{t^{2}}}$$  
可以看出，这个导函数是单减的。意味着，虽然 $F(x)$是单增的，但增加的会越来越慢，随着我们分配到某条河的时间越来越多，我们的收益（y轴方向上位移的增量）会越来越少。所以，在某个时刻，某条河将不是最优解，它的增速将与其他的一些河相同，我们这时就会向那几条河同时分配时间，随着时间推移，又会有更多的河流的增速与它们一样。。。

以此类推，当我们可以游到对岸时，最后一定有一种时间分配方案使得每条河的导函数函数值相同（为什么最后一定会相同，博主也有点没搞懂），所以，我们二分所有河导函数相同的那个函数值，代入反解出所有河分配的时间，求出总和，如果还有多余时间就改小函数值，否则增大。。。以此类推，二分几次就能得出最优解（因为是浮点数）。

看起来求导部分就是最毒瘤的了，然而反解部分依然毒瘤的一匹。。。

我们将函数值x代入等式：

$$x=\frac{u^{2}t}{\sqrt{u^{2}t^{2}-w^{2}}}+v$$

接下来一波化简（前方高能预警）：

$x\sqrt{u^{2}t^{2}-w^{2}}=u^{2}t+v\sqrt{u^{2}t^{2}-w^{2}}$
$(x-v)\sqrt{u^{2}t^{2}-w^{2}}=u^{2}t$
$(x^{2}+v^{2}-2xv)(u^{2}t^{2}-w^{2})=u^{4}t^{2}$
$x^2u^2t^2-x^2w^2+v^2u^2t^2-w^2v^2-2xvu^2t^2+2xvw^2=u^4t^2$
$u^2t^2(x^2-2xv+v^2)-w^2(x^2-2xv+v^2)=u^4t^2$
$u^2t^2(x-v)^2-w^2(x-v)^2=u^4t^2$

设 $R=x-v$代入原式：    

$u^2t^2R^2-w^2R^2=u^4t^2$
$(u^2R^2-u^4)t^2=w^2R^2$
$t^2=\frac{w^2R^2}{u^2R^2-u^4}$

终于，大功告成，可以开始码了：  
$$t=\sqrt{\frac{w^2R^2}{u^2R^2-u^4}}$$
最后，为了防止被卡精度，我们使用的是long double，但是这个东西在windows上运行会有妙妙的效果，博主本地样例输出-1，交上去AC。。。

代码

#include<bits/stdc++.h>
#define db long double
using namespace std;
struct sd{db v,w,t;};
const int M=55;
int n;
db totw,le,ri,mid,u,t;
sd riv[M];
db sqr(db x){return x*x;}
void in()
{
    scanf("%d%Lf%Lf",&n,&u,&t);
    for(int i=1;i<=n;++i)
    scanf("%Lf%Lf",&riv[i].w,&riv[i].v),totw+=riv[i].w,le=max(le,riv[i].v);
}
db check(db x)
{
    db r=0,hh;
    for(int i=1;i<=n;++i)
    {
        hh=(x-riv[i].v)*(x-riv[i].v);
        riv[i].t=sqrt((hh*sqr(riv[i].w))/(hh*sqr(u)-sqr(u)*sqr(u)));
        r+=riv[i].t;
    }
    return r;
}
void ac()
{
    le+=u;ri=1e12;
    if(totw/u>t)printf("-1"),exit(0);
    for(int i=1;i<=5000;++i)
    {
        mid=(le+ri)*0.5;
        if(check(mid)>=t)le=mid;
        else ri=mid;
    }
    check(le);
    db toth=0;
    for(int i=1;i<=n;++i)toth+=sqrt(sqr(u*riv[i].t)-sqr(riv[i].w))+riv[i].v*riv[i].t;
    printf("%.3Lf\n",sqrt(sqr(totw)+sqr(toth)));
    for(int i=1;i<=n;++i)printf("%.3Lf ",riv[i].t);
}
int main()
{
    in();ac();
    return 0;
}