深度学习：神经风格转移

风格转移简介

简单来讲，就是将想绘制的内容，从写实派转化为别的艺术风格，为了方便表述，我们约定想绘制的内容为C，想学习的风格为S，最后生成的作品为G，可以从下图直观的感受风格转移：

要实现神经风格转移，我们先直观地感受一下CNN的网络中究竟发生了什么。

直观感受CNN

让我们以下图展示的CNN为例：

先从第一层开始，对于第一层中的某个单元，我们寻找最能激活它的九个图块（因为浅层的这些单元只能接收到很小的一块图像），可以发现这些单元感知的都是一些色块或边缘（线条）这种简单的图像特征：

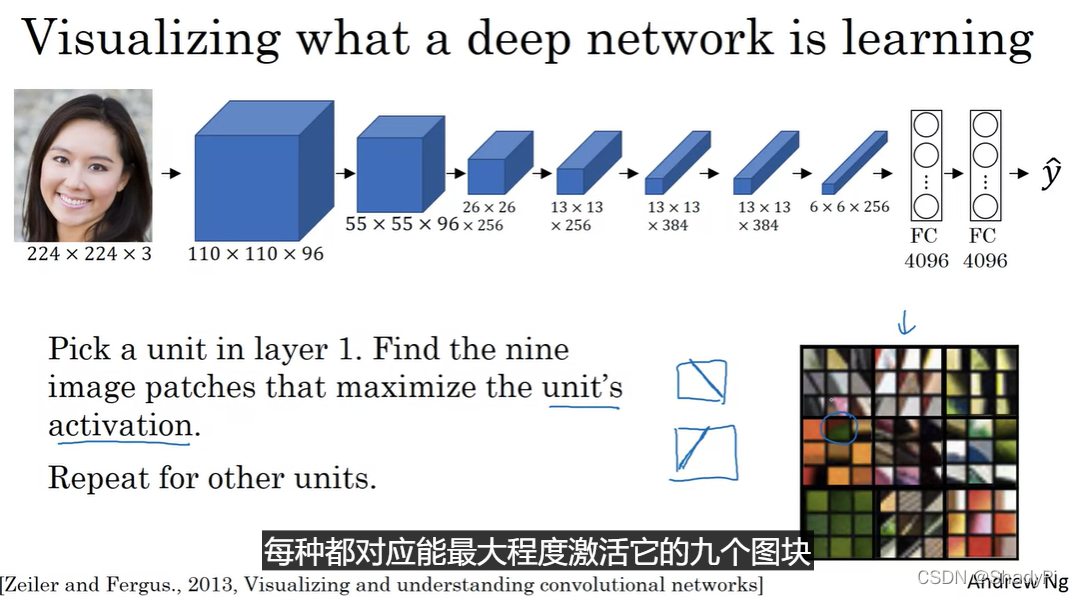
随着网络的深入，我们发现单元感知的图像变得越来越大，不仅是从图片规模上，而且在概念层面也变得越来越“大”且复杂：

代价函数

众所周知，搭建学习算法离不开代价函数，通过最小化代价函数，我们能让神经网络的输出越来越接近我们想要的结果，那么如何为风格转移构造代价函数呢？

我们希望在输出G中实现的目标有两个：一是包含我们想画的内容C，二是我们想拥有的风格S。所以，代价函数也有两部分构成，内容代价函数$J_{\text{content}}(C,G)$用于评判G绘制C的情况，而风格代价函数$J_{style}(S,G)$则评价G是否有S“內味儿”。我们通过两个超参数$\alpha$和$\beta$来调整内容与风格这两个指标的比重，最终表达式为
$$J(G)=\alpha J_{\text{c}}(C,G)+\beta J_s(S,G)$$（用两个超参数来调整内容与风格的相对比重似乎有点多余，但是风格转移原作者就是这么干的）

大概的运算流程就是先随机生成一张雪花图，之后通过梯度下降之类的算法最小化$J(G)$，逐渐得到一张绘制了内容C，但是风格趋近于S的作品。

接下来让我们看看怎么具体地实现两个代价函数。

内容代价函数

内容代价函数相较风格代价函数而言要简单一些，我们要做的就是选择一个已经训练过的CNN（如VGG），向该网络中分别输入C和G，然后在网络中比较中间的位置挑选一个隐藏层$a^{[l]}$，比较这两张图片在这个隐藏层上的差别，即
$$J_c(C,G)=||a^{[l](C)}-a^{[l](G)}|{|}^2$$
注意如果$l$选的太浅，得到的G像素值会跟C非常相似，而如果$l$太深，得到的G可能在画面元素上跟C有些相似（比如都有狗，有一滩水），但就看不出画的是同一个内容了。

风格代价函数

用中间隐藏层的激活值计算内容代价还算好理解，那么在网络中“风格”究竟是怎样捕捉的呢？我们的定义是激活层中位置相同但通道不同的单元激活值之间的相关系数。从上一大节我们可以看到，在中间的隐藏层会识别一些纹路、色彩等信息，而相关系数就是计算这些元素同时出现的概率。比如条纹纹理和蓝色的相关系数高，那么就说明风格S倾向于蓝色条纹。

具体来讲，假设我们选择了第$l$个隐藏层，这个矩阵的大小为$n_H\times n_W\times n_C$，那么这一层的相关系数为
$$\begin{gathered} G_{k{k}^{\prime }}^{[l](S)}=\sum _{i=1}^{n_H}\sum _{j=1}^{n_W}{a}_{ijk}^{[l](S)}{a}_{ij{k}^{\prime }}^{[l](S)} \\ {G}_{k{k}^{\prime }}^{[l](G)}=\sum _{i=1}^{n_H}\sum _{j=1}^{n_W}{a}_{ijk}^{[l](G)}{a}_{ij{k}^{\prime }}^{[l](G)} \\ {J}_s^{[l]}(S,G)=\frac{1}{(2n_H{n}_W{n}_C{)}^2}\sum _{k=1}^{n_C}\sum _{k^{\prime }=1}^{n_C}(G_{k{k}^{\prime }}^{[l](S)}-G_{k{k}^{\prime }}^{[l](G)}{)}^2 \end{gathered}$$
其中，矩阵G计算的是某两个通道之间的相关系数，又被称为格拉姆矩阵（gram matrix），而常数项没有那么重要，因为最后都可以通过参数$\beta$调整。

如果想让风格的计算更准确，我们可以考虑多个隐藏层，赋予每个隐藏层不同的权重${\lambda }^{[l]}$，最后的风格代价函数写为
$$J_s(S,G)=\sum _l{\lambda }^{[l]}{J}_s^{[l]}(S,G)$$使得风格可以综合考虑来自浅层和深层的更多信息。