跑6公里用了30分钟（好像稍微快了点ORT），那么这个过程的平均速度是
3.33m/s
先来看看这3.33m/s的计算过程
6
K
m
30
m
i
n
=
200
m
1
m
i
n
=
3.33
m
1
s
\frac{6Km}{30min} = \frac{200m}{1min} = \frac{3.33m}{1s}
30min6Km=1min200m=1s3.33m
从上述看，只要不断缩短时间，直到0，应该就可以定义某个瞬间的速度。
一、引入
在x轴上t时刻位于x(t), t' 时刻位于 x(t')
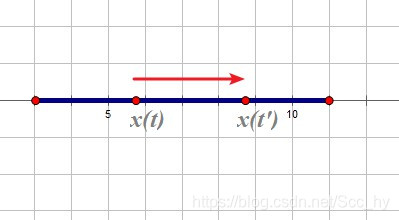
则该段期间的移动平均速度为：
x
(
t
′
)
−
x
(
t
)
t
′
−
t
\frac{x(t')- x(t)}{t'-t}
t′−tx(t′)−x(t)
如果两者时间间隔不断缩进：
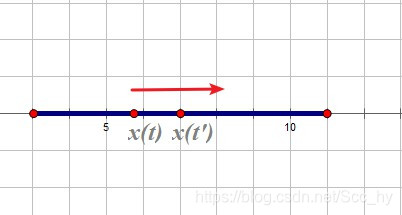
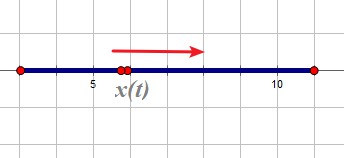
可见缩短时间间隔t'-t ，前进距离 x(t')- x(t)也逐渐逼近0。
若间隔为0，则t' = t ，x(t') = x(t)，
平均移动速度就算时候，分母为t'-t, 那么可以假设x(t') = x(t) = t^2 用分子消掉：
x
(
t
′
)
−
x
(
t
)
t
′
−
t
=
t
′
2
−
t
2
t
′
−
t
=
(
t
′
−
t
)
(
t
′
+
t
)
t
′
−
t
=
t
′
+
t
=
2
t
\frac{x(t')- x(t)}{t'-t} = \frac{t'^2- t^2}{t'-t} =\frac{(t'-t)(t'+t)}{t'-t} = t'+t = 2t
t′−tx(t′)−x(t)=t′−tt′2−t2=t′−t(t′−t)(t′+t)=t′+t=2t
微分定义为：
d
x
d
t
=
lim
t
′
→
t
x
(
t
′
)
−
x
(
t
)
t
′
−
t
\frac{\rm dx}{\rm dt} =\lim_{t'\rightarrow t} \frac{x(t')- x(t)}{t'-t}
dtdx=t′→tlimt′−tx(t′)−x(t)
在求极限的时候要将分子分母视为一体，此时的"瞬间速度"才有意义，不然除以0那么该速度没有意义
二、微分是积分的逆运算
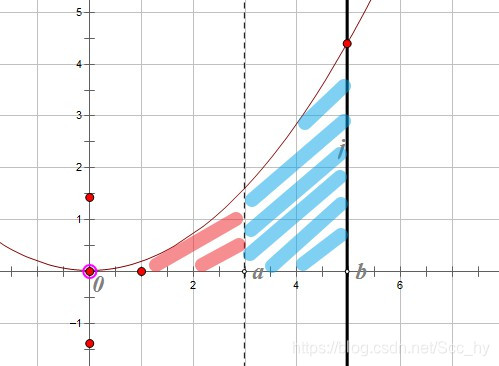
整体面积 = 红色面积 + 蓝色面积
用积分表示为:
∫
0
b
f
(
x
)
d
x
=
∫
0
a
f
(
x
)
d
x
+
∫
a
b
f
(
x
)
d
x
\int _0^b{f(x)\rm{d} x} = \int _0^a{f(x)\rm{d} x} + \int _a^b{f(x)\rm{d} x}
∫0bf(x)dx=∫0af(x)dx+∫abf(x)dx
将右边的第一个式子移到左边：
∫
0
b
f
(
x
)
d
x
−
∫
0
a
f
(
x
)
d
x
=
∫
a
b
f
(
x
)
d
x
\int _0^b{f(x)\rm{d} x} - \int _0^a{f(x)\rm{d} x} = \int _a^b{f(x)\rm{d} x}
∫0bf(x)dx−∫0af(x)dx=∫abf(x)dx
将微分定义带入：
d
d
a
∫
0
a
f
(
x
)
d
x
=
lim
a
′
→
a
∫
0
a
f
(
x
)
d
x
−
∫
0
a
′
f
(
x
)
d
x
a
−
a
′
=
lim
a
′
→
a
∫
a
′
a
f
(
x
)
d
x
a
−
a
′
\frac{\rm d}{\rm da} \int _0^a{f(x)\rm{d} x}=\lim_{a'\rightarrow a} \frac{\int _0^{a}{f(x)\rm{d} x}- \int _0^{a'}{f(x)\rm{d} x}}{a-a'}=\lim_{a'\rightarrow a}\frac{\int _{a'}^{a}{f(x)\rm{d} x}}{a-a'}
dad∫0af(x)dx=a′→alima−a′∫0af(x)dx−∫0a′f(x)dx=a′→alima−a′∫a′af(x)dx
最终主要求分子的值，即求a'接近 a 的时候的面积是多少
由于积分可以知道a与a' 十分接近的时候，其面积为(a-a') * f(a')
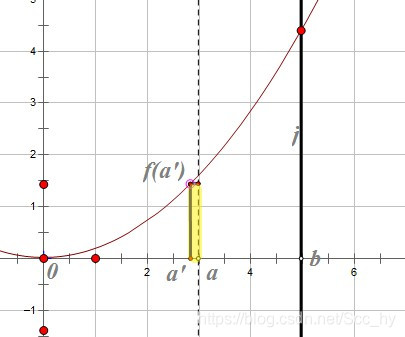
所以式子可以转化为：
d
d
a
∫
0
a
f
(
x
)
d
x
=
lim
a
′
→
a
∫
a
′
a
f
(
x
)
d
x
a
−
a
′
=
(
a
−
a
′
)
∗
f
(
a
′
)
a
−
a
′
=
f
(
a
′
)
=
f
(
a
)
\frac{\rm d}{\rm da} \int _0^a{f(x)\rm{d} x}=\lim_{a'\rightarrow a}\frac{\int _{a'}^{a}{f(x)\rm{d} x}}{a-a'} =\frac{(a-a') * f(a')}{a-a'}=f(a')=f(a)
dad∫0af(x)dx=a′→alima−a′∫a′af(x)dx=a−a′(a−a′)∗f(a′)=f(a′)=f(a)
【注：dx = (a - 0) / n = a - a'】
可以发现，对积分进行微分后重新返回了原函数。反之，如果对函数进行微分再积分，那么又回到最初的状态
牛顿和莱布尼茨的"微积分学基本定理"指的就是微分和积分的逆运算
∫ b a d f ( x ) d x d x = f ( b ) − f ( a ) \int _b^a \frac{\rm df(x)}{\rm dx} {\rm{d} x}=f(b) - f(a) ∫badxdf(x)dx=f(b)−f(a)
三、指数的微分
f ( x ) = e x f(x) = e^x f(x)=ex 的微分
lim
x
′
→
x
e
x
′
−
e
x
x
′
−
x
=
lim
x
′
→
x
(
e
x
′
−
x
−
1
)
e
x
x
′
−
x
\lim_{x'\rightarrow x}\frac{e^{x'} - e^x}{x' -x} = \lim_{x'\rightarrow x}\frac{(e^{x' - x} - 1)e^x}{x' -x}
x′→xlimx′−xex′−ex=x′→xlimx′−x(ex′−x−1)ex
因为x' - x ⇒ 0 所以e^(x' - x) ⇒ e^0 ，所以e^(x' - x) - 1⇒ e^0 -1 ⇒ 0
所以：
lim
x
′
→
x
e
x
′
−
e
x
x
′
−
x
=
e
x
\lim_{x'\rightarrow x}\frac{e^{x'} - e^x}{x' -x} = e^x
x′→xlimx′−xex′−ex=ex
可见 e^x 的微分就是其本身
-
根据"微积分学基本定理" ：
- 对积分进行微分后重新返回了原函数。反之，如果对函数进行微分再积分，那么又回到最初的状态。
所以可以求得e^x 的积分如下：
∫
a
b
d
e
x
d
x
d
x
=
∫
a
b
e
x
d
x
=
e
b
−
e
a
\int _a^b{\frac{\rm de^x}{dx}}\rm{d} x=\int _a^b e^x \rm{d} x = e^b - e^a
∫abdxdexdx=∫abexdx=eb−ea
扫一扫
1076
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
