时间复杂度对比:
Prim:O(n2)O(n^2)O(n2) 适用于稀疏图
Prim + 优先队列(堆优化):O((n+m)∗logm)O((n + m) * logm)O((n+m)∗logm)
Kruskal:O(m∗logm+mα(n))O(m*logm + mα(n))O(m∗logm+mα(n)),α(n)α(n)α(n)为常数 适用于稠密图
PSPSPS:文末附三者算法效率分析..................
Prim + 邻接链表:
#include<bits/stdc++.h>
#define rint register int
#define deb(x) cerr<<#x<<" = "<<(x)<<'\n';
using namespace std;
typedef long long ll;
typedef pair <int,int> pii;
const ll mod = 1e9 + 7;
const int maxn = 2e5 + 10;
int n, m, cnt, ans, dis[maxn];
int head[maxn], vis[maxn];
struct EDGE{
int next, to, w;
} e[maxn<<1];
inline int read(){
int x=0;
char ch=getchar();
while(ch>'9' || ch<'0') ch=getchar();
while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
return x;
}
void add(int u, int v, int w) {
e[++cnt].next = head[u];
e[cnt].w = w;
e[cnt].to = v;
head[u] = cnt;
}
void prim(int st){
memset(vis,0,sizeof(vis));
for(int i=1; i<=n; i++) dis[i] = INT_MAX;
for(int i=head[st]; i; i=e[i].next)
dis[e[i].to] = min(dis[e[i].to], e[i].w);
dis[st] = 0, vis[st] = 1;
for(int i=1; i<n; i++){
int tmp = INT_MAX, k = 0;
for(int j=1; j<=n; j++)
if(!vis[j] && tmp>dis[j]){
k = j;
tmp = dis[j];
}
vis[k] = 1;
ans += tmp;
for(int j=head[k]; j; j=e[j].next)
if(!vis[e[j].to] && dis[e[j].to]>e[j].w)
dis[e[j].to] = e[j].w;
}
}
int main() {
n = read(), m = read();
memset(head,0,sizeof(head));
ans = cnt = 0;
for(int i=0; i<m; i++){
int u, v, w;
u = read(), v = read(), w = read();
add(u, v, w);
add(v, u, w);
}
prim(1);
printf("%d\n", ans);
}
Prim + 邻接链表 + 堆优化(优先队列):
#include<bits/stdc++.h>
#define rint register int
#define deb(x) cerr<<#x<<" = "<<(x)<<'\n';
using namespace std;
typedef long long ll;
typedef pair <int,int> pii;
const ll mod = 1e9 + 7;
const int maxn = 2e5 + 10;
int n, m, cnt, ans, vis[maxn];
int head[maxn], dis[maxn];
priority_queue <pii, vector<pii>, greater<pii> > q;
struct EDGE{
int next, to, w;
} e[maxn<<1];
inline int read(){
int x=0;
char ch=getchar();
while(ch>'9' || ch<'0') ch=getchar();
while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
return x;
}
void add(int u, int v, int w) {
e[++cnt].next = head[u];
e[cnt].w = w;
e[cnt].to = v;
head[u] = cnt;
}
void prim(int st){
memset(vis,0,sizeof(vis));
for(int i=1; i<=n; i++) dis[i] = INT_MAX;
q.push(make_pair(0, st));
dis[st] = 0;
int num = 0;
while(!q.empty() && num<n){
int d = q.top().first;
int k = q.top().second;
q.pop();
if(vis[k]) continue;
num++;
ans += d;
vis[k] = 1;
for(int i=head[k]; i; i=e[i].next)
if(e[i].w<dis[e[i].to]){
dis[e[i].to] = e[i].w;
q.push(make_pair(e[i].w, e[i].to));
}
}
}
int main() {
n = read(), m = read();
memset(head,0,sizeof(head));
ans = cnt = 0;
for(int i=0; i<m; i++){
int u, v, w;
u = read(), v = read(), w = read();
add(u, v, w);
add(v, u, w);
}
prim(1);
printf("%d\n", ans);
}
Kruskal:
#include<bits/stdc++.h>
#define rint register int
#define deb(x) cerr<<#x<<" = "<<(x)<<'\n';
using namespace std;
typedef long long ll;
typedef pair <int,int> pii;
const ll mod = 1e9 + 7;
const int maxn = 2e5 + 10;
int n, m, cnt, ans, f[maxn];
struct EDGE{
int u, v, w;
bool operator <(const EDGE &A) const{
return w<A.w;
}
} e[maxn];
inline int read(){
int x=0;
char ch=getchar();
while(ch>'9' || ch<'0') ch=getchar();
while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
return x;
}
int find(int x){
return x == f[x] ? x : f[x] = find(f[x]);
}
int main() {
int u, v, w;
n = read(), m = read();
for(int i=1; i<=n; i++) f[i] = i;
for(int i=0; i<m; i++){
e[i].u = read();
e[i].v = read();
e[i].w = read();
}
sort(e, e+m);
for(int i=0; i<m; i++){
u = find(e[i].u);
v = find(e[i].v);
if(u!=v){
f[u] = v;
ans += e[i].w;
cnt++;
}
if(cnt==n-1) break;
}
printf("%d\n", ans);
}
附上Prim,Prim+heap,Kruskal算法效率分析 (用堆优化就完事了呗):
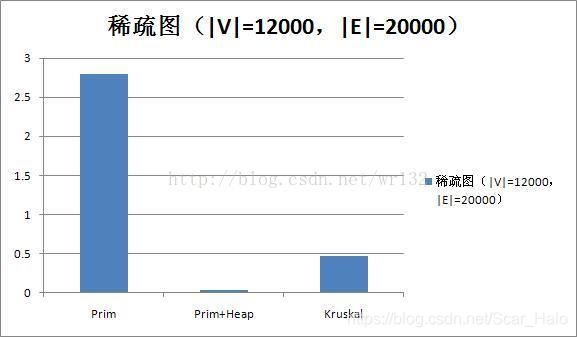
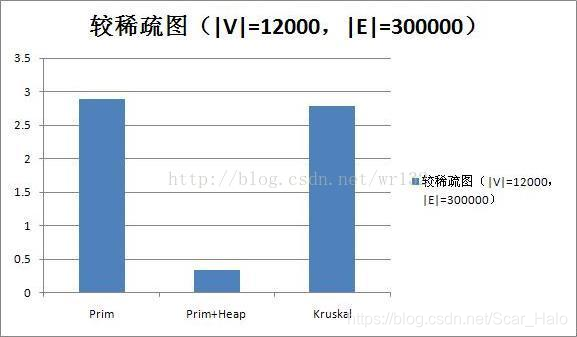
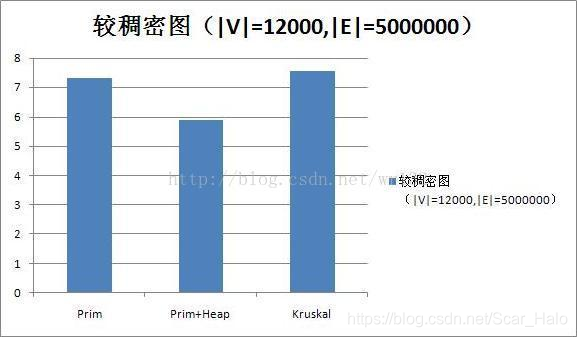
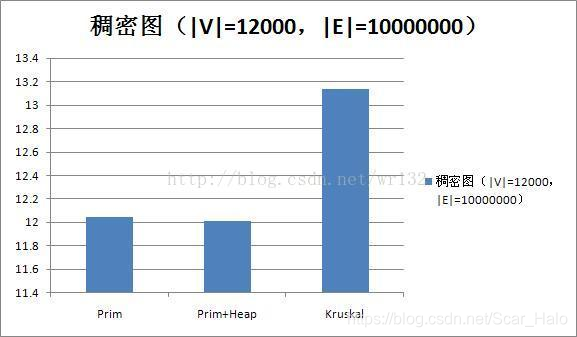
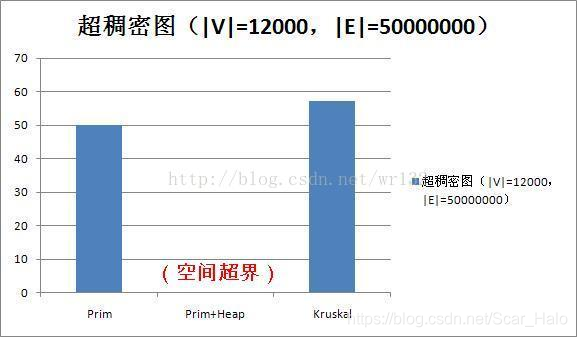








 博客主要介绍了Prim和Kruskal两种最小生成树算法,包含Prim结合邻接链表、Prim结合邻接链表与堆优化(优先队列)以及Kruskal算法。还给出了各算法的时间复杂度,Prim适用于稀疏图,Kruskal适用于稠密图,文末附算法效率分析。
博客主要介绍了Prim和Kruskal两种最小生成树算法,包含Prim结合邻接链表、Prim结合邻接链表与堆优化(优先队列)以及Kruskal算法。还给出了各算法的时间复杂度,Prim适用于稀疏图,Kruskal适用于稠密图,文末附算法效率分析。
















 1864
1864

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








