Lec1
Pseudo code 伪代码
Primitive Operations 计算基本操作


Recursive Algorithm 递归算法

e.g Fibonacci

1)用递归写

2)用for循环写

Lec2
Asymptotic notation 渐近符号
渐近符号允许表征影响运行时的主要因素
-
O(n):表示算法的渐进上界。如果一个算法的运行时间是O(n),那么它的运行时间最多与输入规模n成正比。换句话说,当输入规模n增加时,算法的运行时间不会超过某个常数倍的n。比如,如果一个算法的时间复杂度是O(n),那么它的运行时间可能是3n,5n,100n等。
-
Ω(n):表示算法的渐进下界。如果一个算法的运行时间是Ω(n),那么它的运行时间至少与输入规模n成正比。换句话说,当输入规模n增加时,算法的运行时间不会比某个常数倍的n小。比如,如果一个算法的时间复杂度是Ω(n),那么它的运行时间可能是n,2n,100n等。
-
Θ(n):表示算法的紧密界限。如果一个算法的运行时间是Θ(n),那么它的运行时间与输入规模n成正比,并且上界和下界是相同的。换句话说,当输入规模n增加时,算法的运行时间将以线性方式增长。比如,如果一个算法的时间复杂度是Θ(n),那么它的运行时间可能是3n,n,100n等,但是不会超过某个常数倍的n。
总之,O(n)描述了算法的最坏情况运行时间上限,Ω(n)描述了最好情况运行时间下限,而Θ(n)描述了最坏情况和最好情况之间的紧密界限。
O(n)
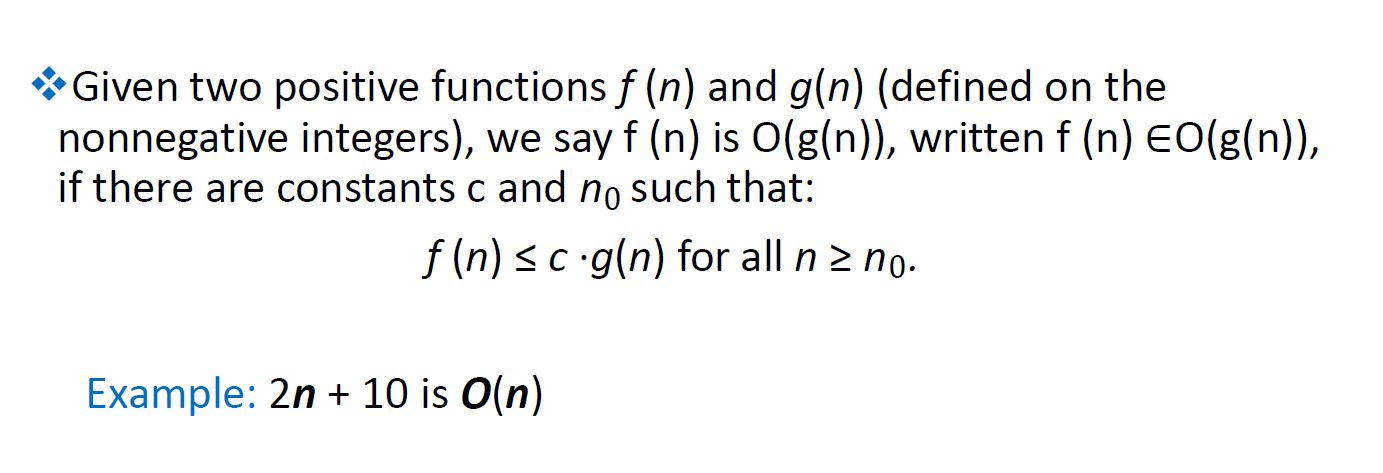


e.g
e.g
Ω(n) and Θ(n)

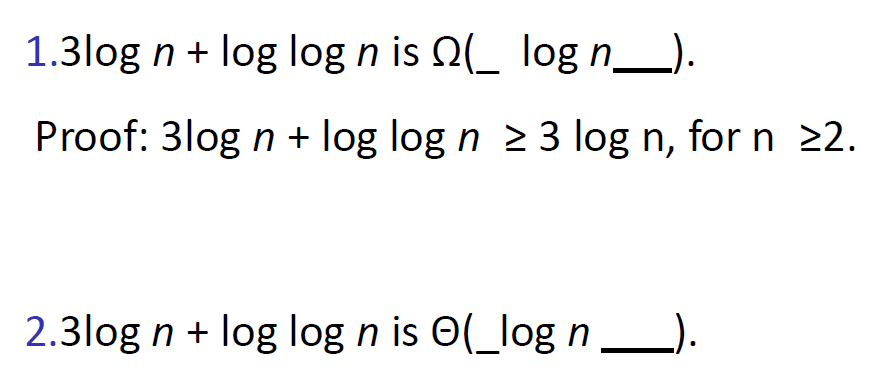
Space Complexity 空间复杂度
空间复杂度是对算法所需的工作存储量的度量。这意味着在最坏的情况下,算法中任意点需要多少内存


Lec3 Data structure
Stack 栈
堆栈是后进先出(Last-In, First-Out)(LIFO)的数据结构
方法

e.g Reversing Aray

Reverse Polishnotation
e.g1

e.g2

e.g3 *
 Exiting a Maze
Exiting a Maze

Queue 队列
队列是先进先出(First-In, First-Out)(FIFO)的数据结构
方法

List 列表
列表是项目的集合,每个项目都存储在一个节点中,节点包含一个数据字段和一个指向下一个元素的指针
方法


Linked List 链表
singly linked list 单链表
单链表中的节点存储指向列表中下一个元素的下一个链接(如果元素是lastelement则为空)。

double linked list 双链表
双链表中的节点存储两个链接:一个next链接,指向列表中的下一个元素,一个prev链接,指向列表中的前一个元素。
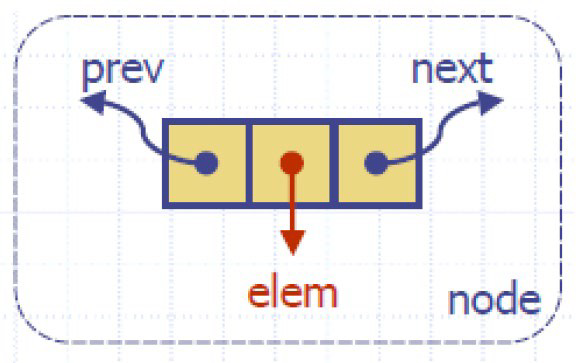
Tree 树
根树T是一组节点,它们以父子关系存储元素
T有一个特殊的节点r,称为根节点ofT。
T的每个节点(根节点r除外)都有一个父节点
如果一个节点没有子节点,它就是叶leaf节点(外部),否则就是叶节点(内部)
方法


Binary Tree
二叉树是一种有根的有序树,其中每个节点最多有两个子节点。
节点深度

节点高度

遍历
前序 preorder
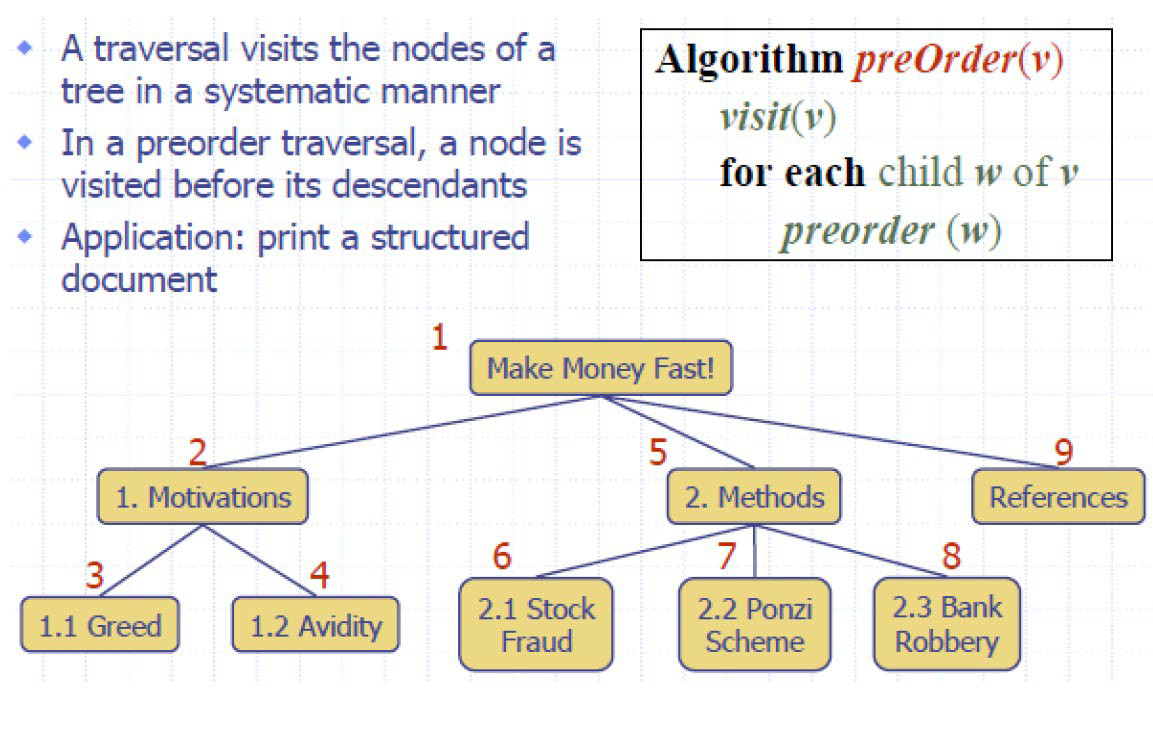

中序 inorder
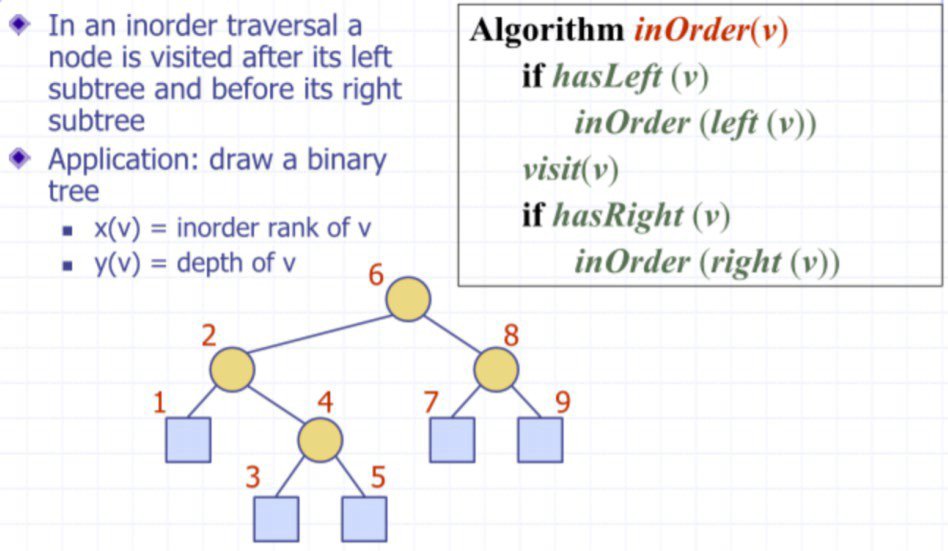

后序 postorder **
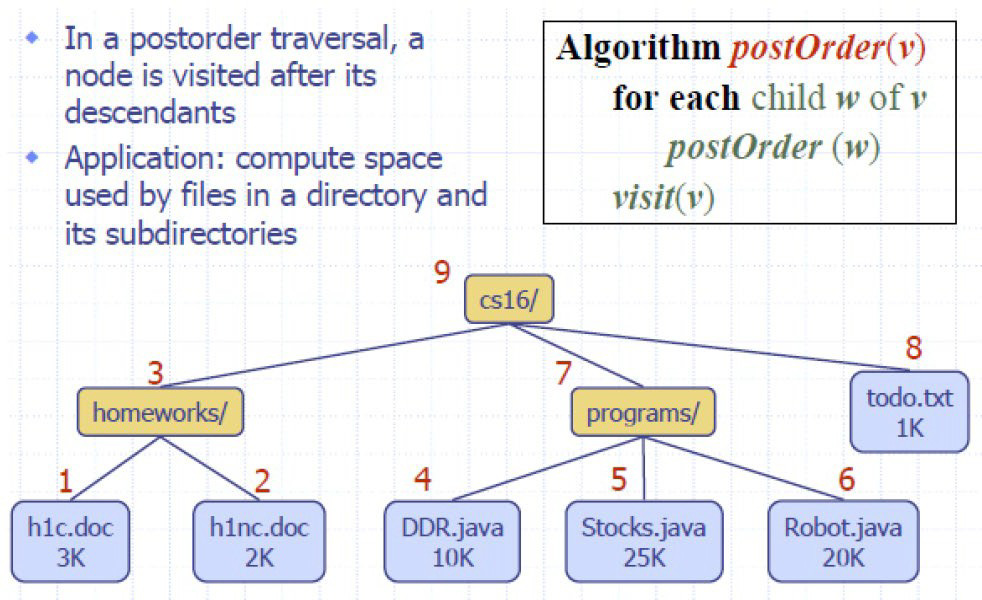
Parsing arithmeticexpressions
每个外部节点是一个变量或常数。
每个内部节点在它的两个子节点上定义一个算术运算
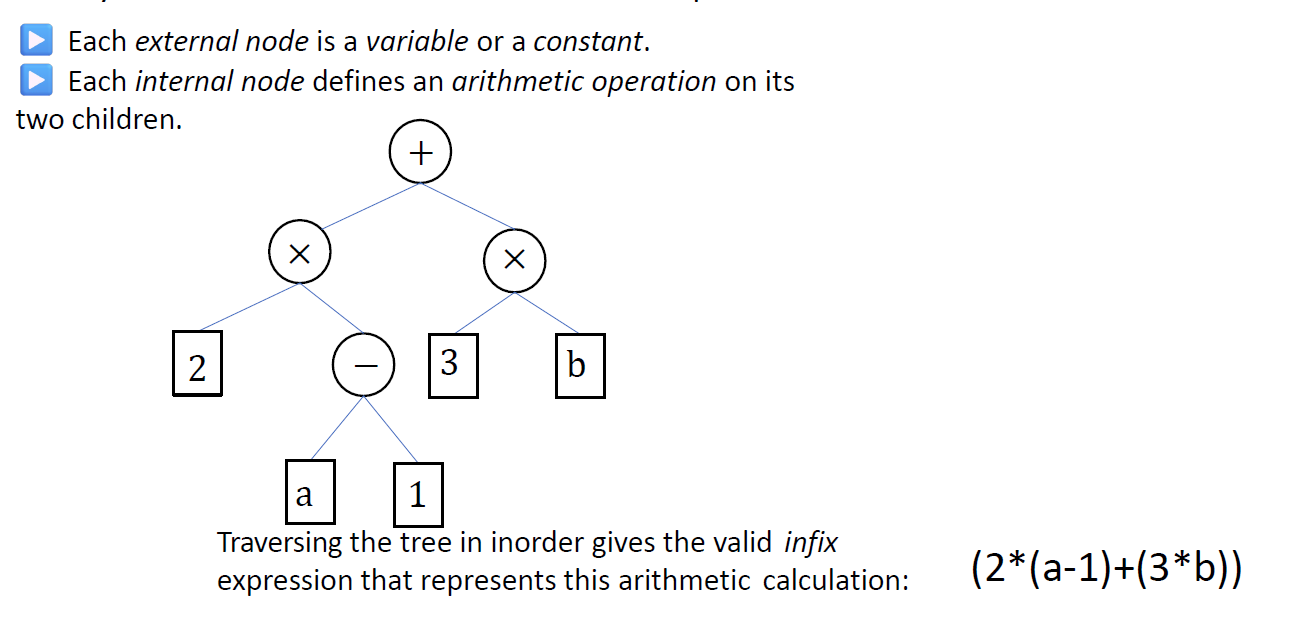
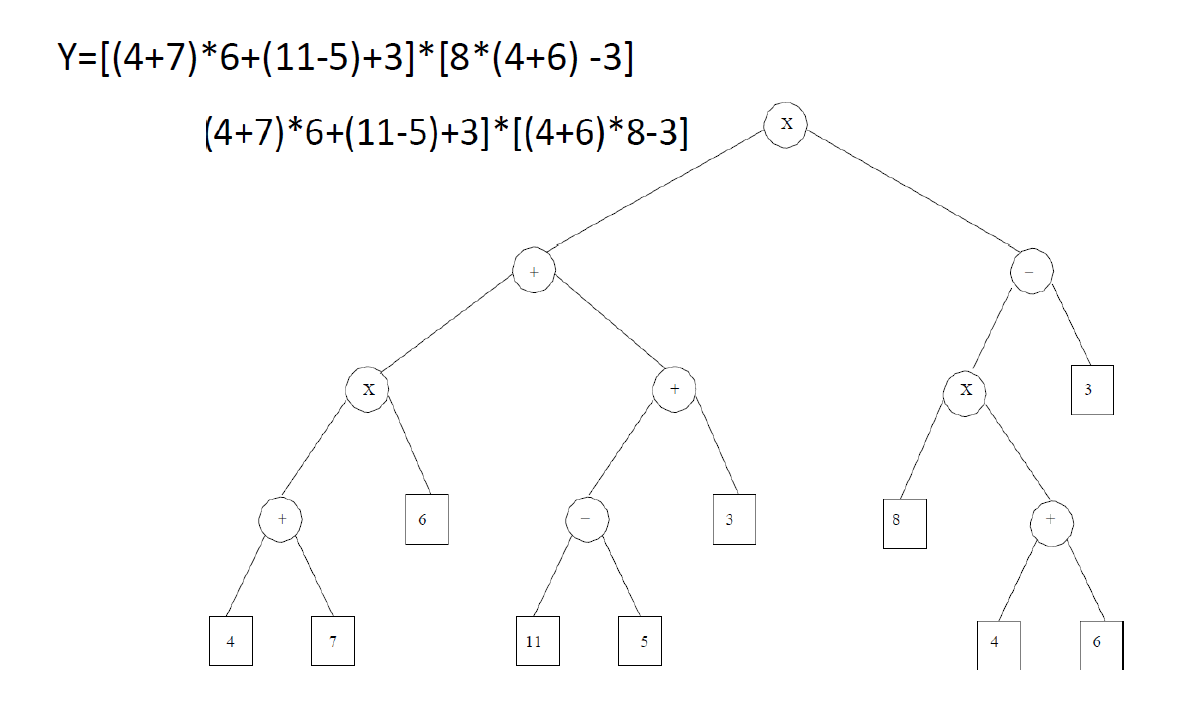
Data structures
链接结构:T的每个节点v由一个对象表示,该对象引用存储在v的元素及其父节点和子节点的位置
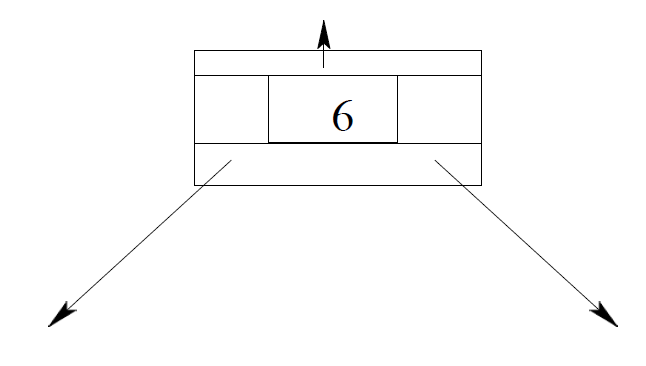
对于每个节点最多有t个子节点且深度有限的有根树,您可以将树存储在数组A中。
一般来说,结点A[i]的两个子结点在A[2 * i + 1]和A[2 * i + 2]。
节点A的父节点[i](根节点除外)为位置A[⌊(i−1)/2⌋]的节点。
Binary Search 二分查找

伪代码

complexity
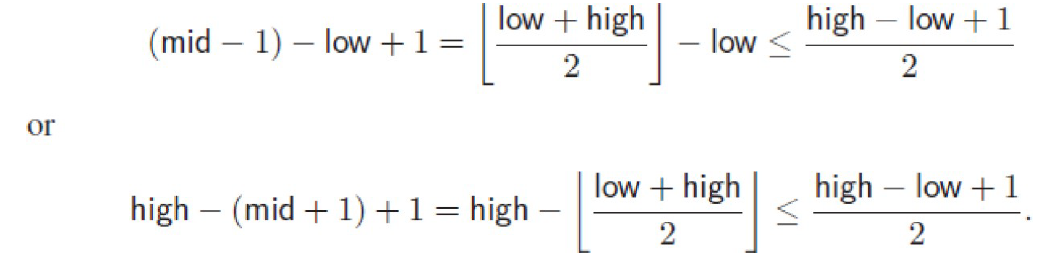

Binary Search Tree 二分查找树
在BST中,每个内部节点存储一个元素e(或者更一般地说,一个定义排序的键k和某个元素)。
BST具有这样的性质:给定一个节点v存储元素e,那么在v处的左子树中的所有元素都小于或等于e,而在v处的右子树中的所有元素都大于或等于toe。
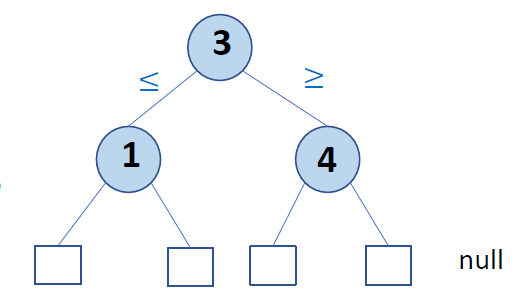
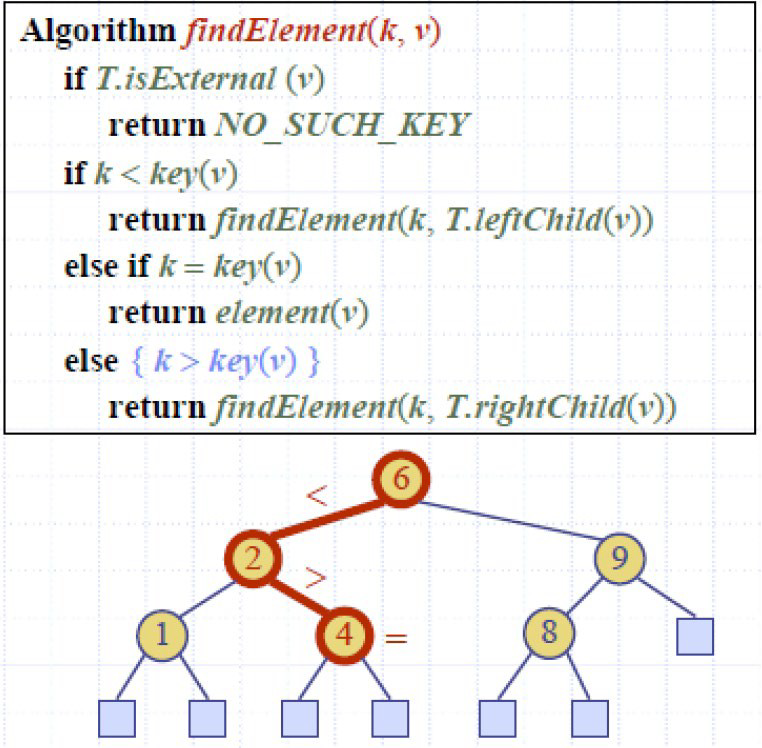
complexity
O(x)
■
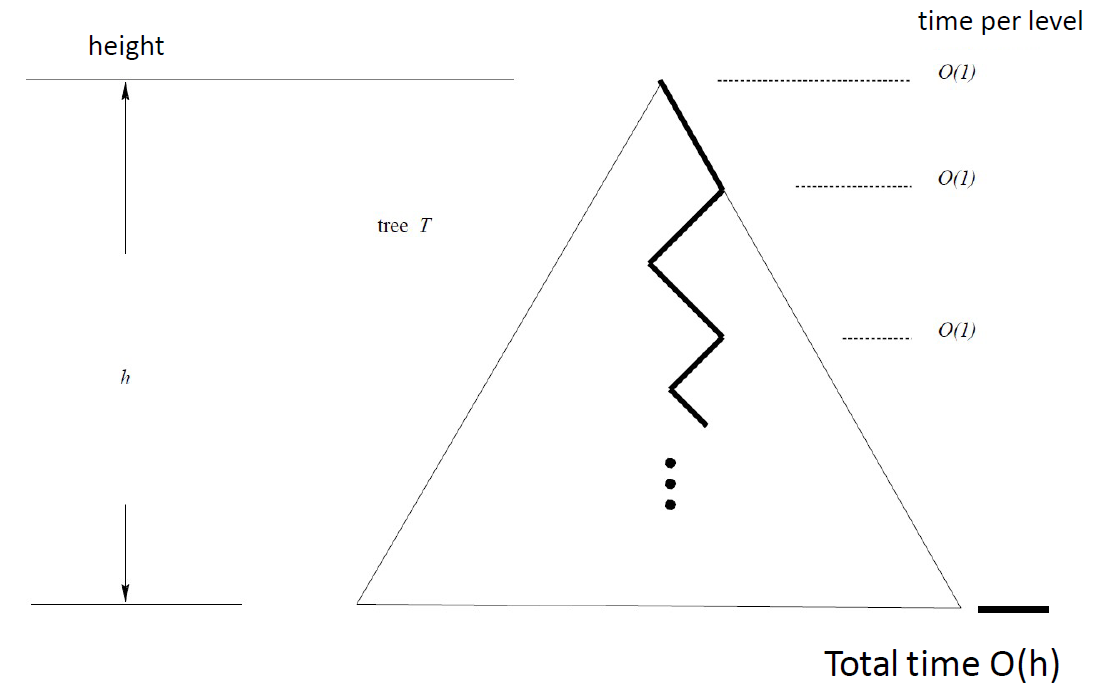
the space used isO(n)
■
method findElementtake O(h)time
•
The height h is O(n) in the worst case and O(log n) in the best case
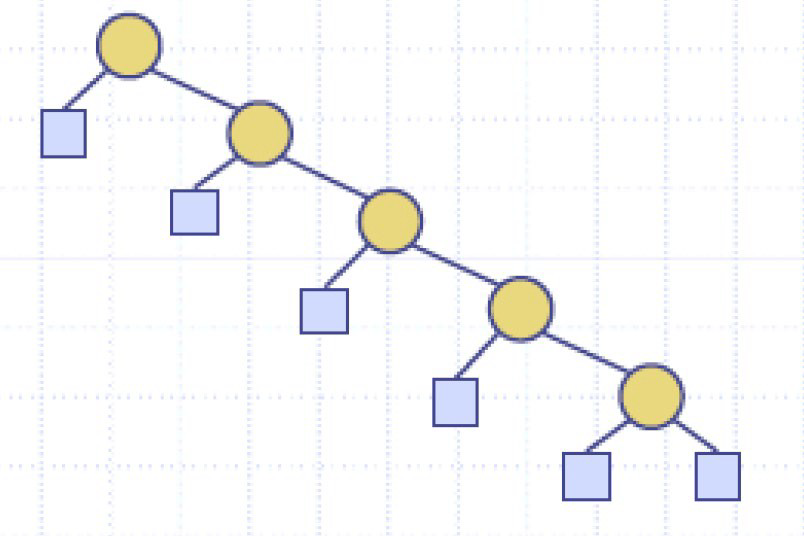

增
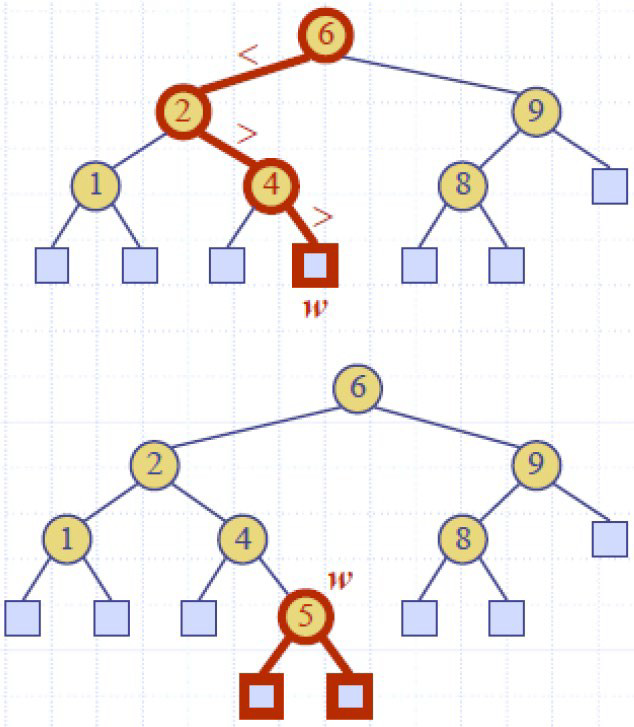

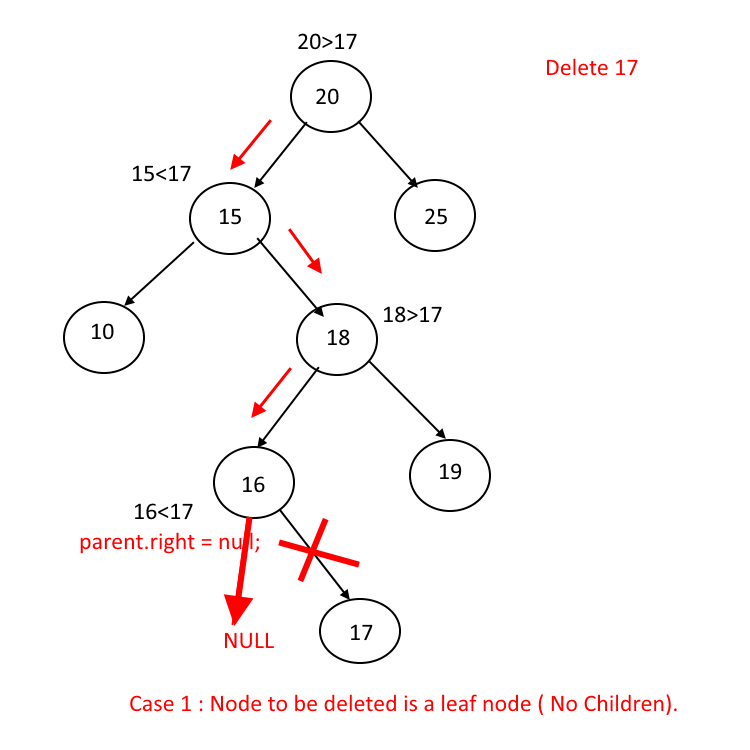
删

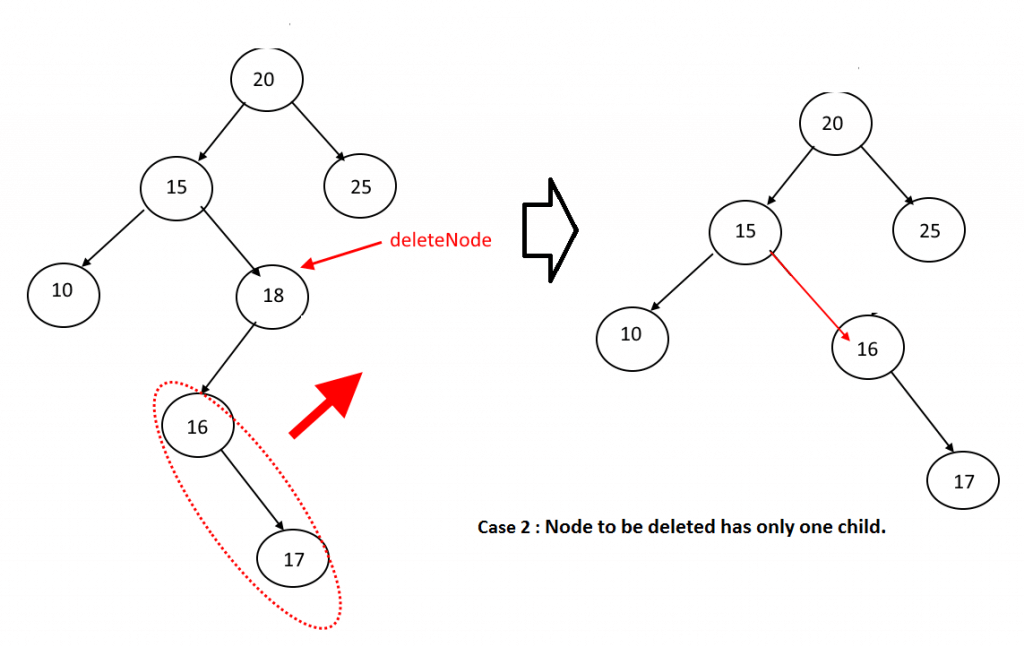

AVL tree 平衡二叉树
Height-Balance属性:对于任何节点n, n的左右子树的高度最多相差1。
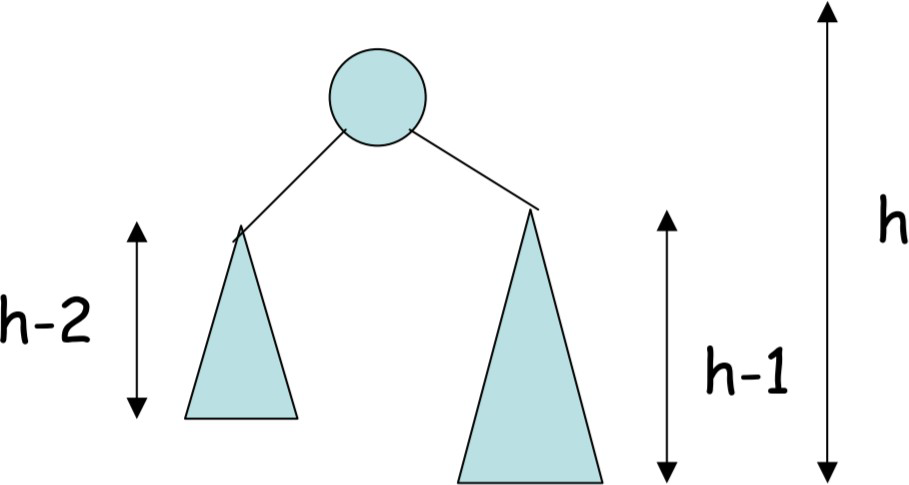
complexity
The height of an AVL tree storing n keys is O(logn).
All operations (search, insertion, and removal) on an AVL tree with n elements can be performed in O(log n)time
插入
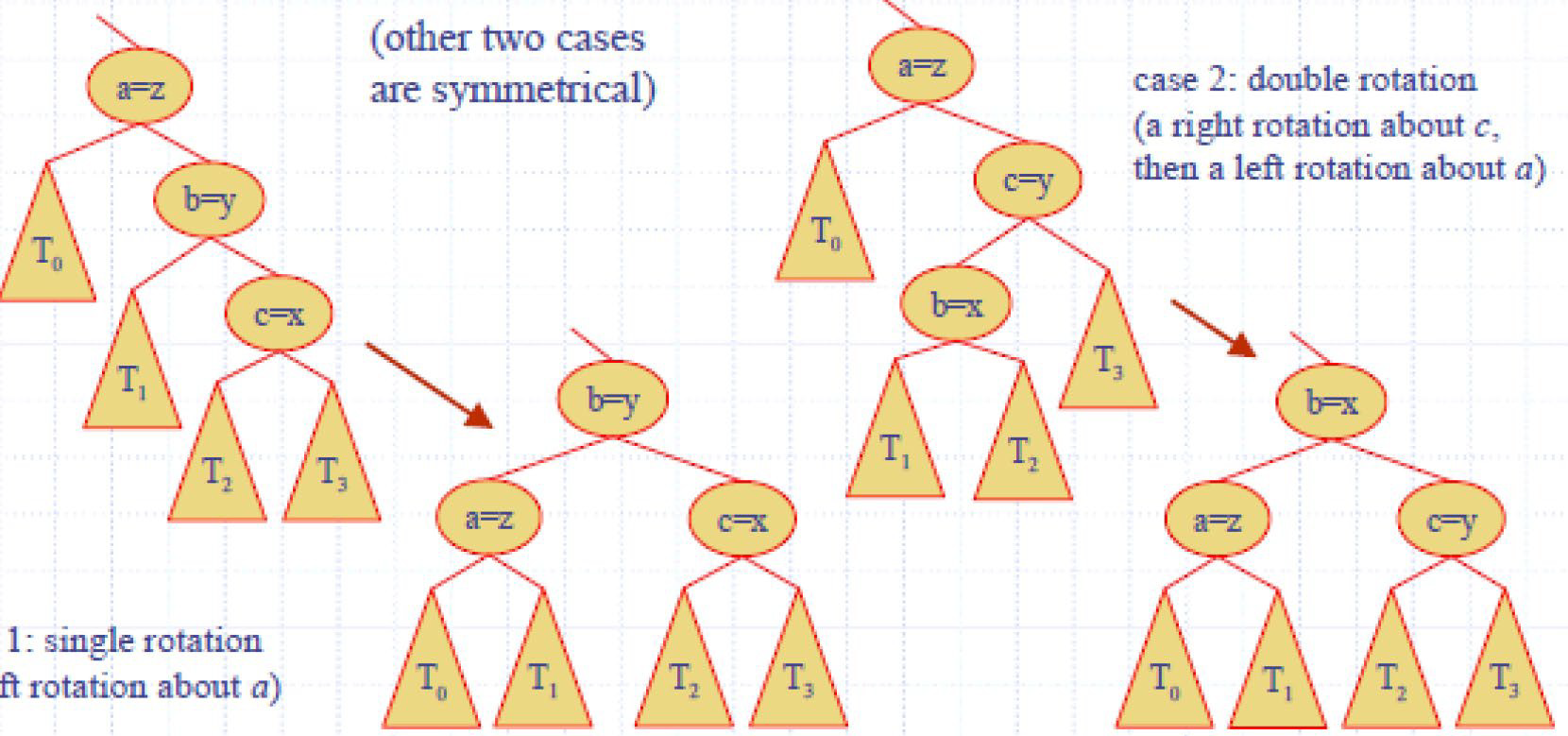
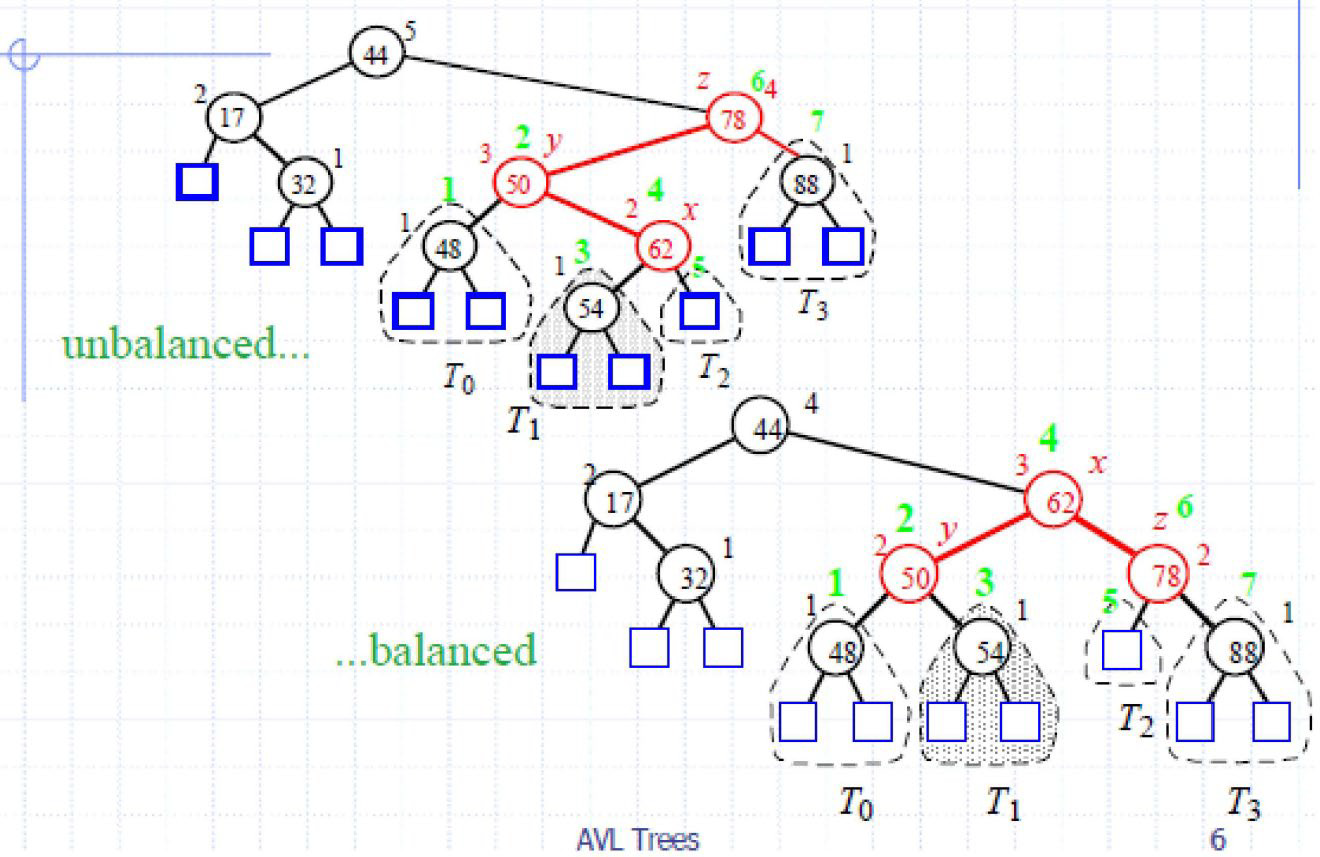
删除
e.g1
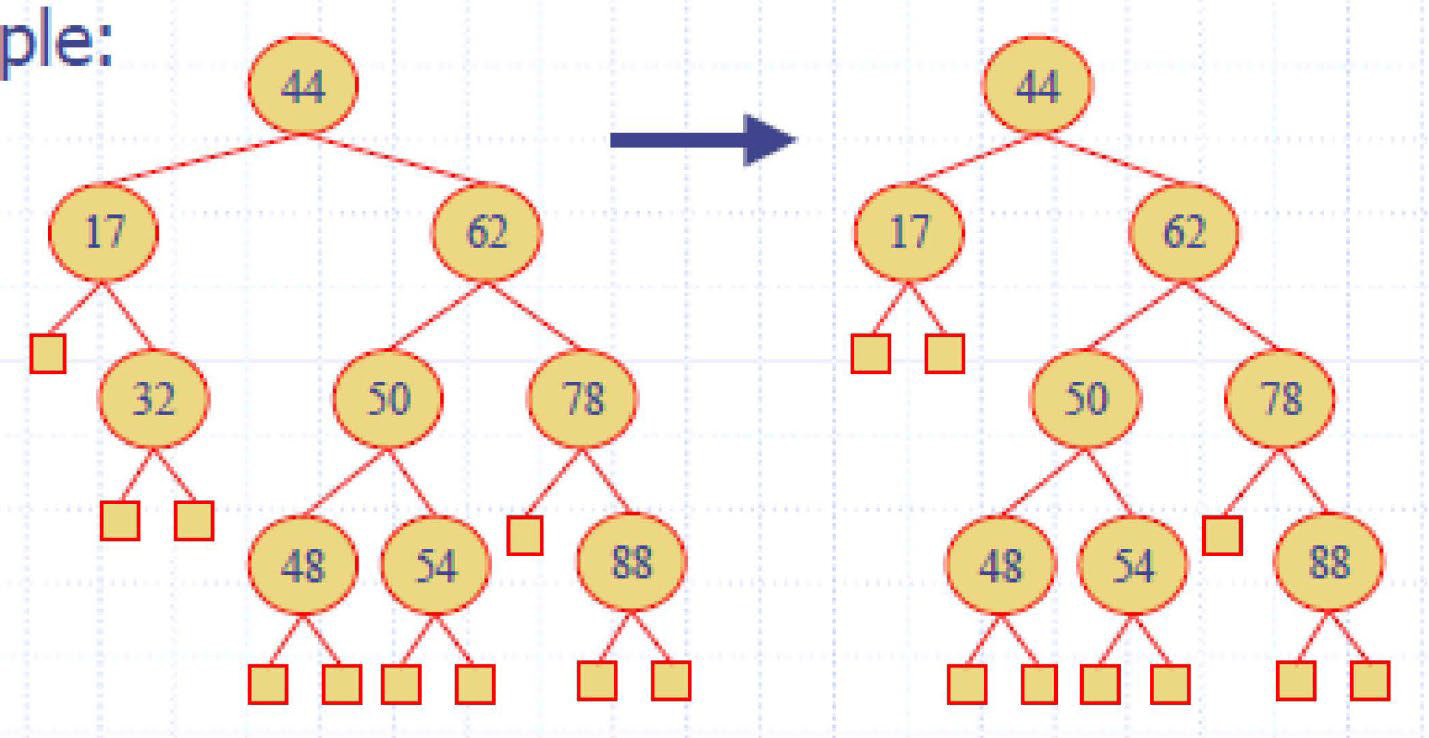
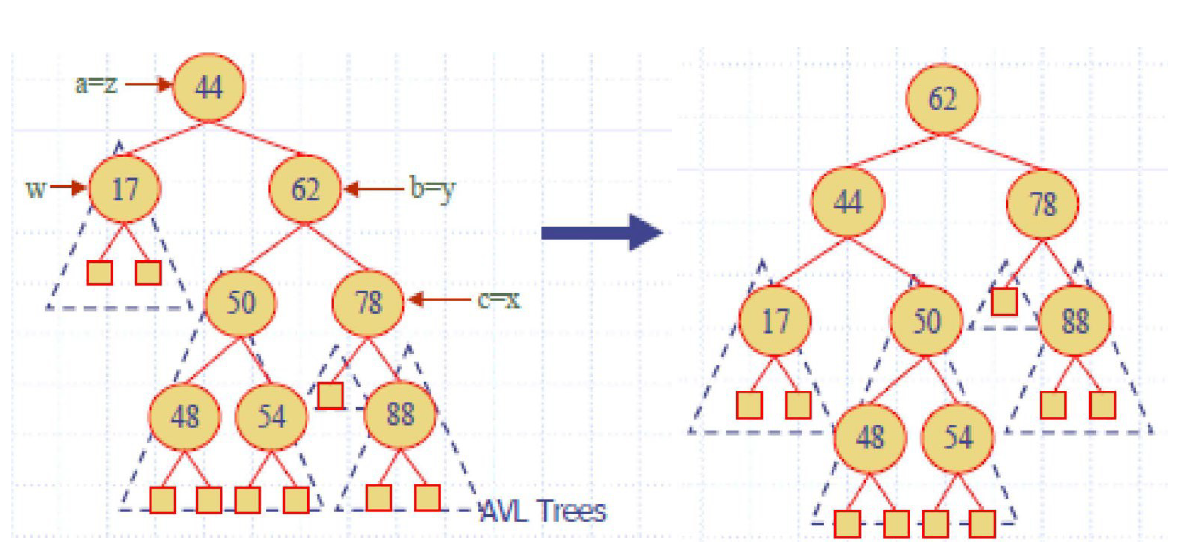
e.g2

Multi-Way Search Tree 多路搜索树
感觉我们其实讲的是B树

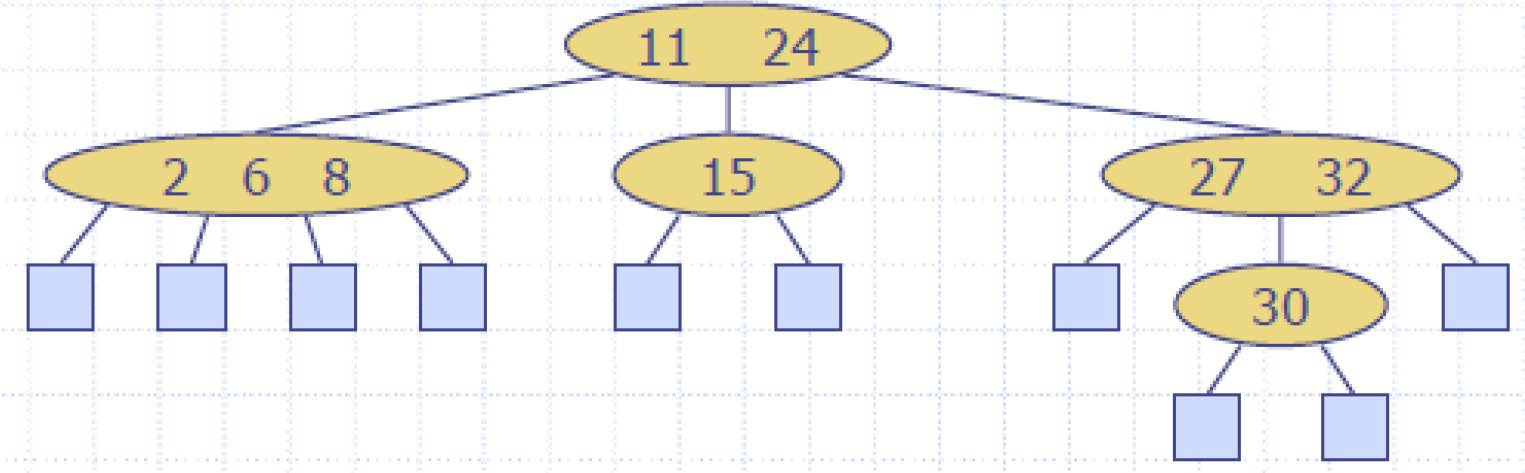

(2,4)树
(2,4)树(也称为2-4树或2-3-4树)是一种多路搜索,具有以下属性:
节点大小属性:每个内部节点最多有四个子节点
深度属性:所有外部节点具有相同的深度
根据子节点的数量,(2,4)树的内部节点被称为2节点、3节点或4节点
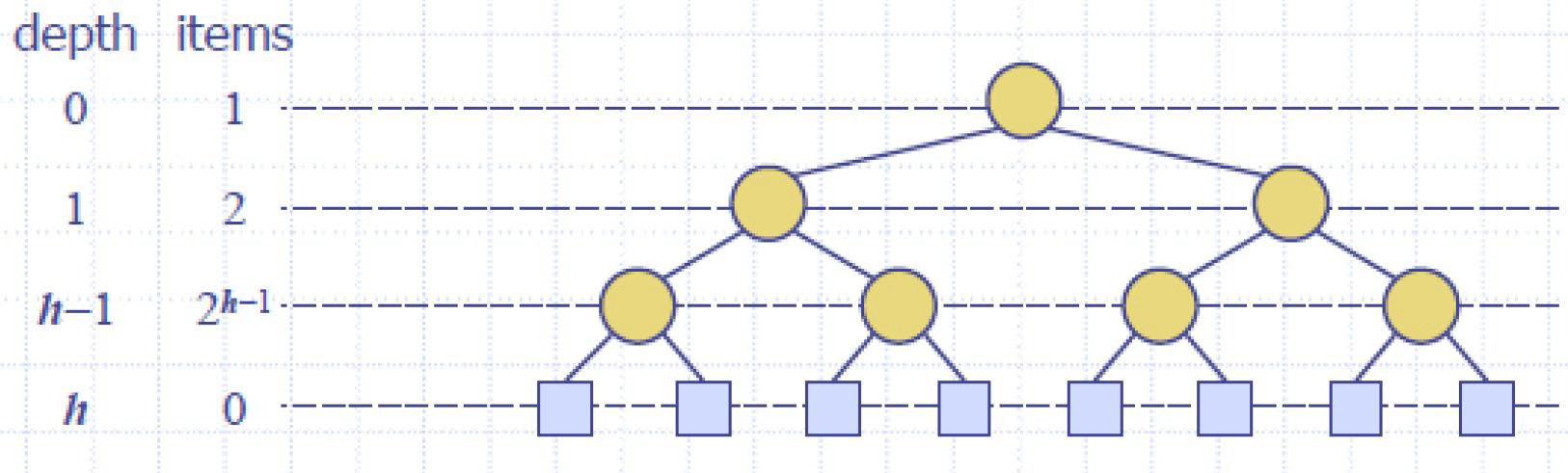
complexity
has height O(logn)
查找 O(logn)
插入


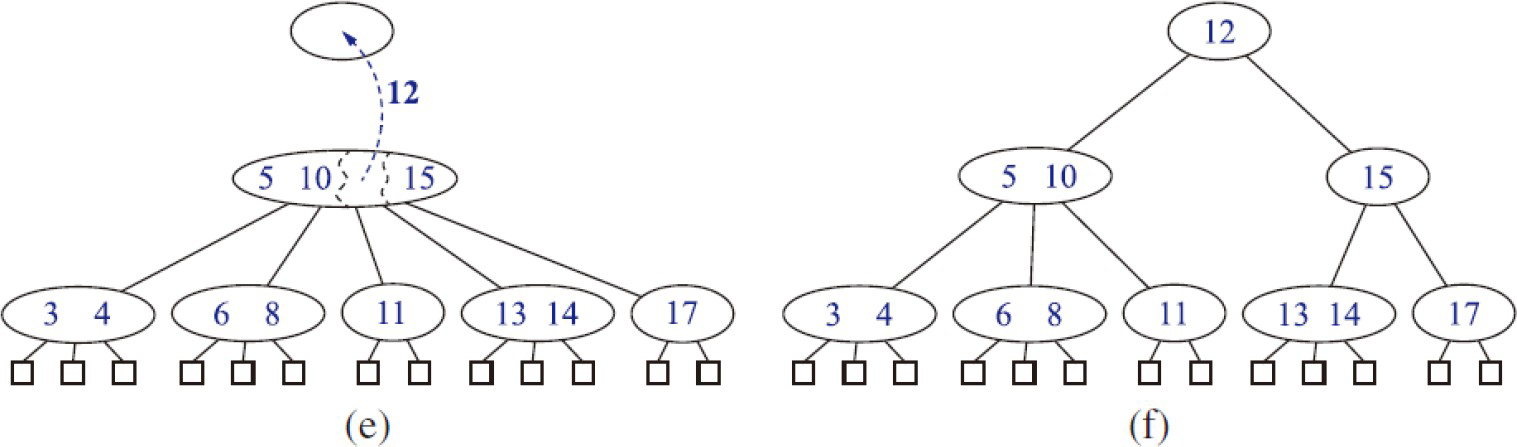 删除
删除



(2,4)树和b树的区别:
-
节点结构:
- (2,4) 树的每个内部节点可以包含 2 到 4 个子节点,并且具有 1 到 3 个关键字。
- B 树的每个节点可以包含更多的子节点,通常在一个节点中可以包含多个关键字,并且子节点数量可以更灵活地调整。
-
平衡要求:
- (2,4) 树要求所有的叶子节点都在同一层级上,并且具有相同数量的关键字。
- B 树没有这样的限制,它允许叶子节点分布在不同的层级,并且子节点数量可以根据需要调整。
Lec4 排序
Priority Queues 优先队列
优先级队列是元素的容器,每个元素都有一个关联的键
方法

第一阶段:通过一系列n个insertItem操作,将C中的元素放入初始为空的优先级队列P中
第二阶段:使用一系列nremoveMin操作从Pin非递减顺序中提取元素。
Heap 堆
堆是优先级队列的一种实现,对于插入和删除都是有效的。
完全二叉树 vs 近似完全二叉树(?)
完全二叉树与满二叉树编号一样

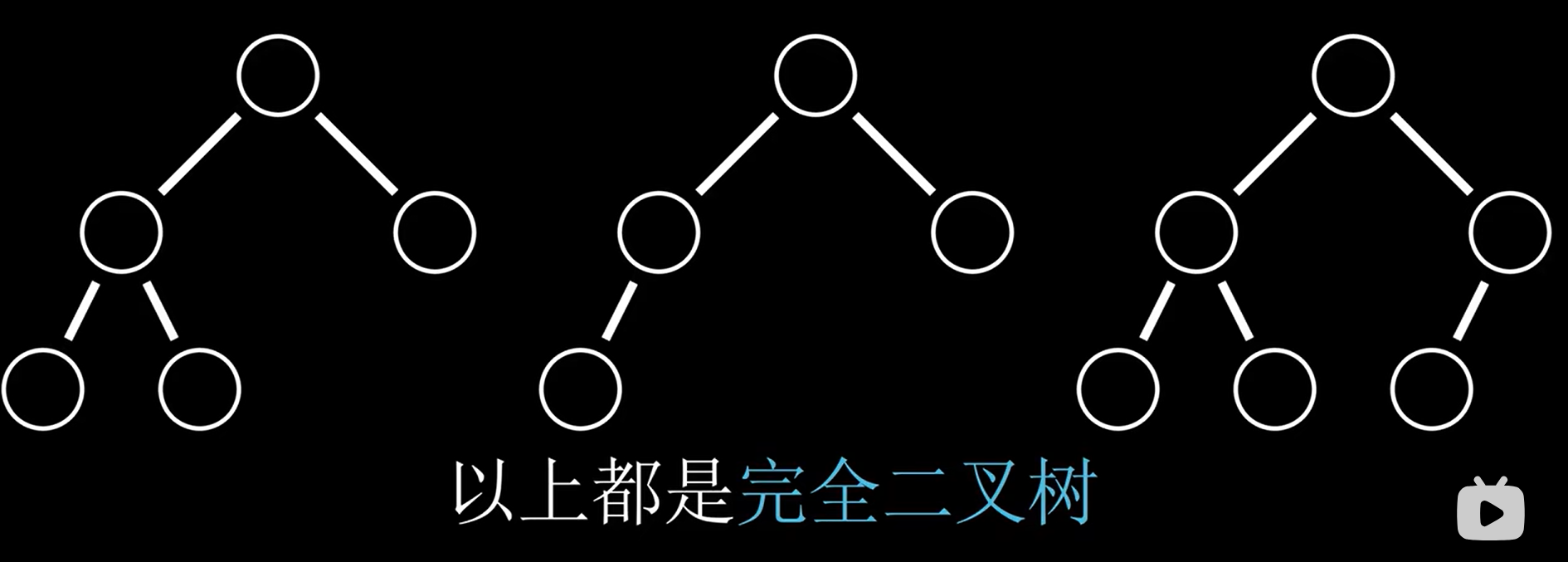
Complete Binary Tree(完全二叉树)vs Nearly Complete Binary Tree(近似完全二叉树)
-
最后一层节点的填充:
- 完全二叉树:最后一层的节点是从左到右依次填充的。
- 近似完全二叉树:最后一层的节点可能不是从左到右完全填充的。
-
结构规律性:
- 完全二叉树:具有较强的结构规律性,每个节点的左右子节点都被填满,除了最后一层。
- 近似完全二叉树:最后一层的节点填充不受严格规定,可能出现缺失节点。
-
性质差异:
- 完全二叉树的性质较为明显,更容易判断和理解。
- 近似完全二叉树的性质相对灵活,更适用于一些实际场景中节点数目不确定的情况。

堆序二叉树Heap-ordered binary tree.
堆是一棵二叉树,在其内部节点上存储键,并满足以下属性:对于每个内部节点v,除了根节点key(v) ≥key(parent(v))
•节点中的键。
•父键不大于子键。
数组表示。
•索引从1开始。
•按等级顺序获取节点。
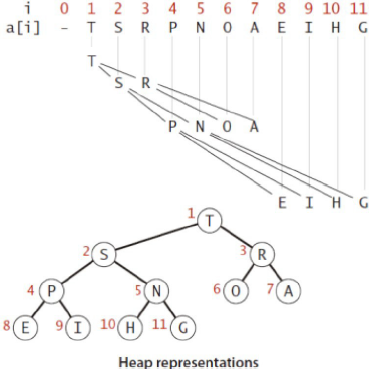
For any given node at position i:
• Its Left Child is at [2*i] if available.
• Its Right Child is at [2*i+1] if available.
• Its Parent Node is at [⌊i/2⌋] if available.
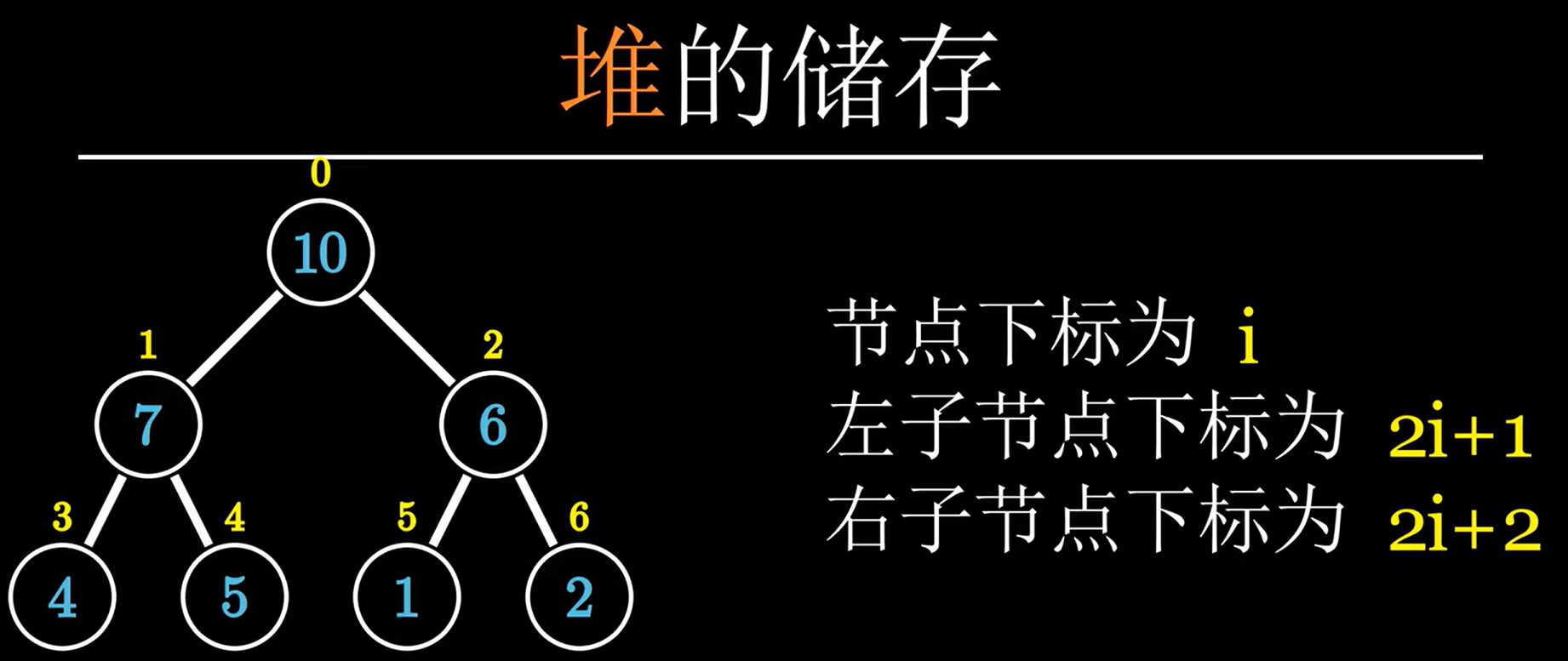
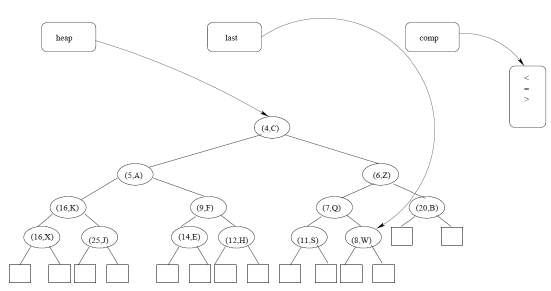
heap:一个(几乎完整的)二叉树T,包含键满足堆顺序属性的元素,存储在数组中。
last:对数组表示中T的最后一个使用节点的引用。
comp:一个比较器函数,它定义键的总顺序关系,用于维护T的根处的最小(或最大)元素。


Up-heap bubbling (insertion) 上滤
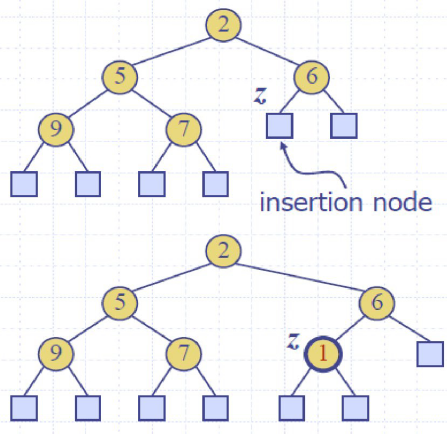
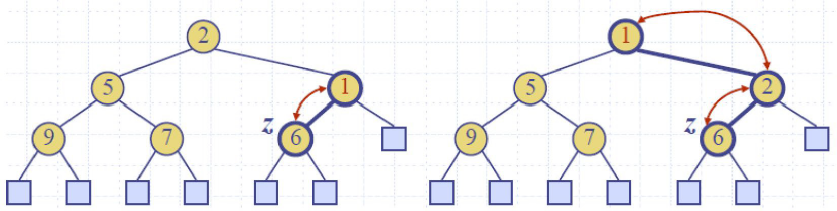
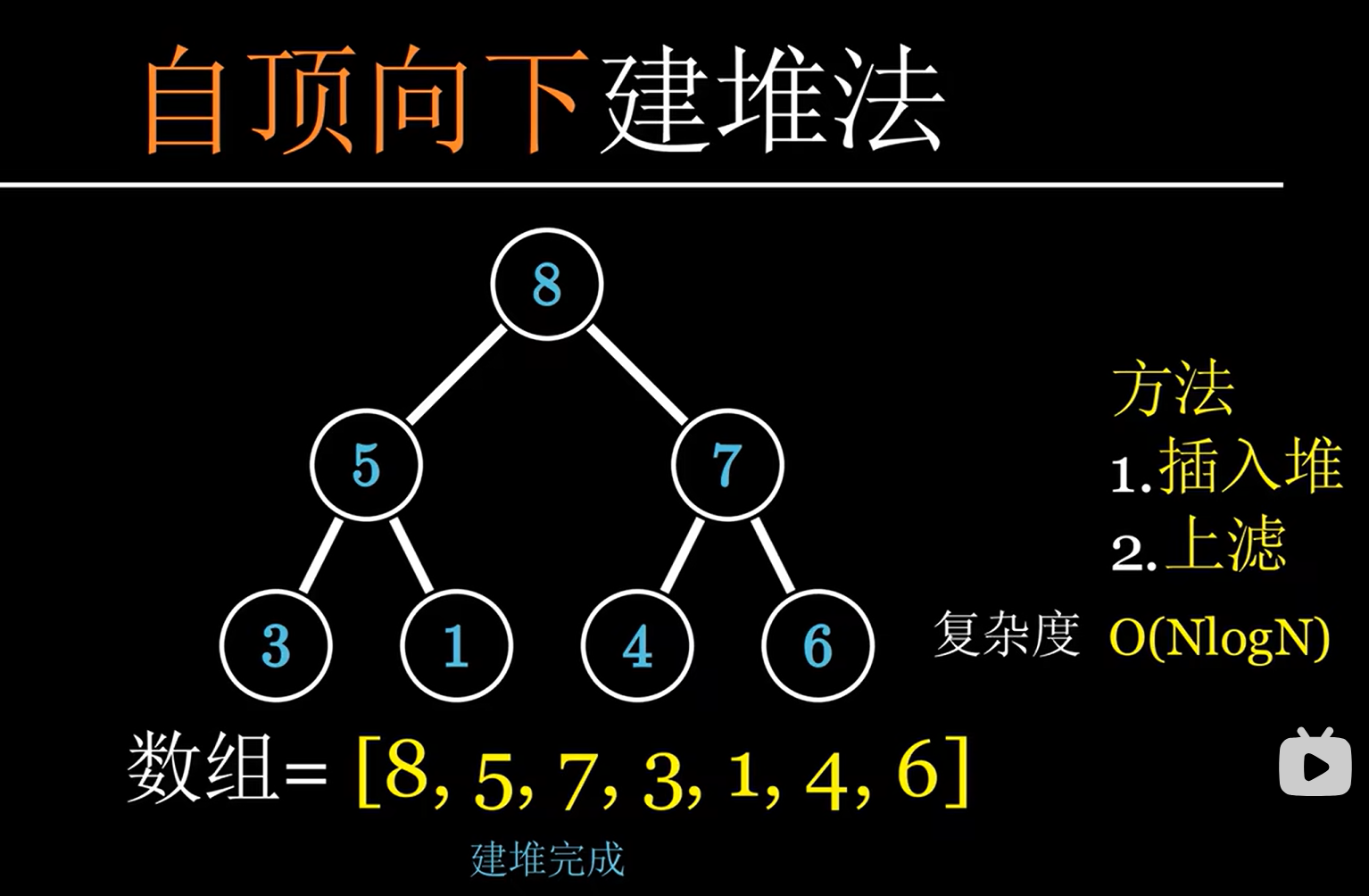
Down-heap bubbling (removal of top element)下滤
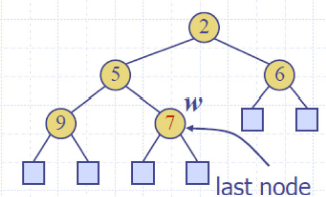
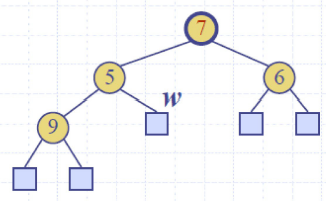
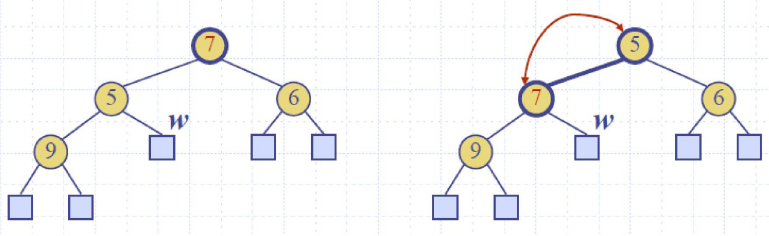
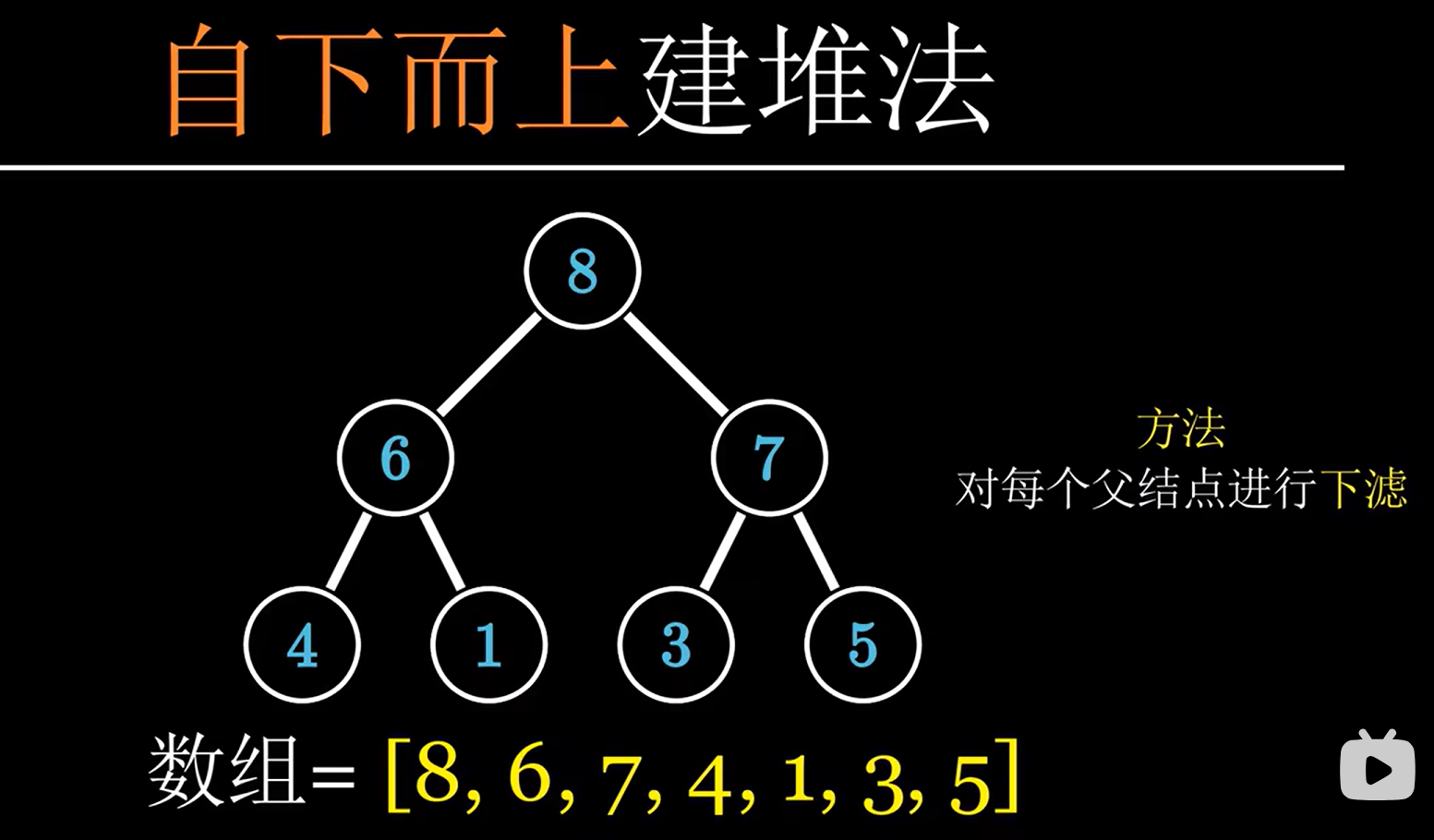
Heap-Sorting
Divide-and-Conquer 分而治之
方法

Master Method
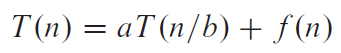
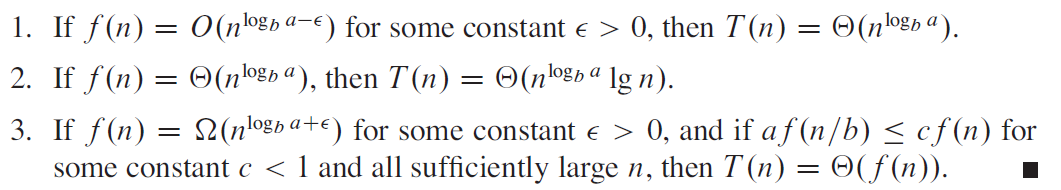
e.g1
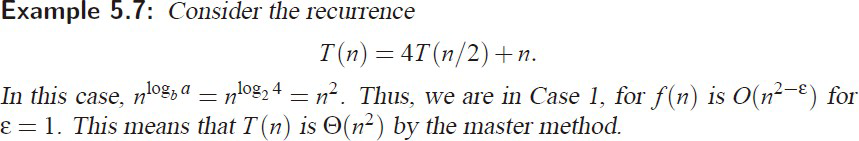
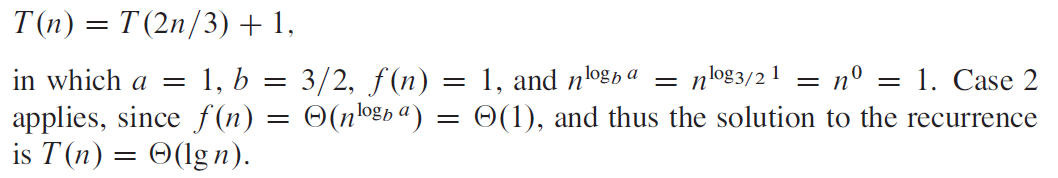
e.g2



e.g3

Matrix Multiplication
Counting inversions
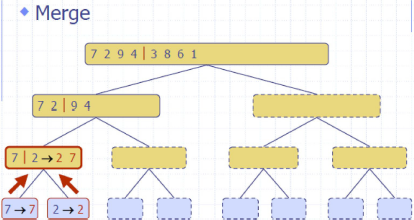
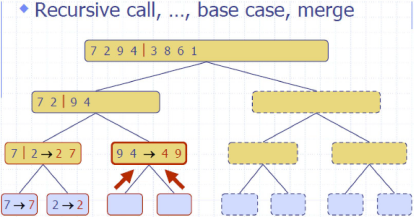
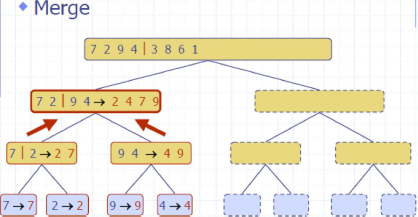
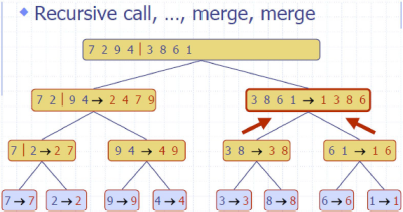
归并排序 MergeSort
Divide: partition 𝑆𝑆 into two sequences 𝑆1and 𝑆2 of about 𝑛/2 elements each
Recur: recursively sort 𝑆1 and 𝑆2
Conquer: merge 𝑆1 and 𝑆2 into a unique sorted sequence

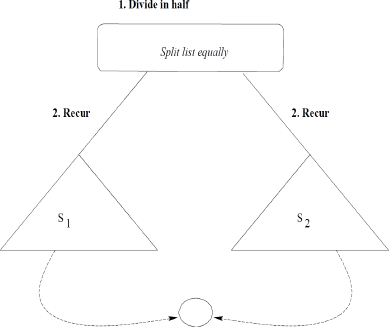
e.g
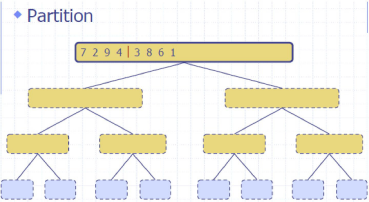
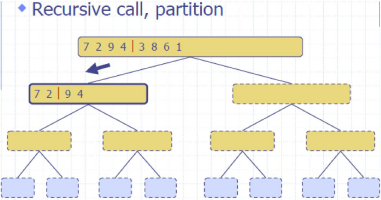
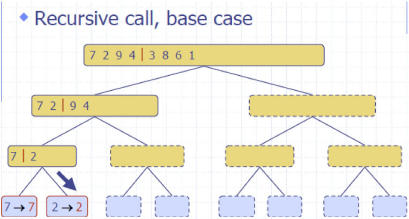
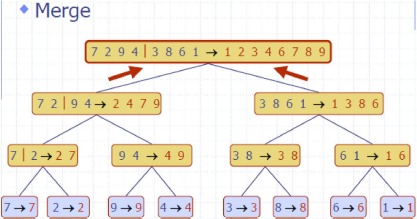
complexity
1. The height ℎ of the merge-sort tree is 𝑂𝑂(log𝑛𝑛)
at each recursive call we divide in half the sequence
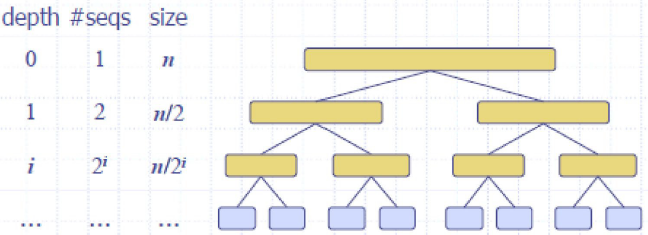
2. The overall amount or work done at the nodes of depth 𝑖𝑖is 𝑂𝑂(𝑛𝑛)
3. Thus, the total running time of merge-sort is 𝑂𝑂 (𝑛𝑛log𝑛𝑛)

快速排序 QuickSort
是基于分而治之范式的随机排序算法:

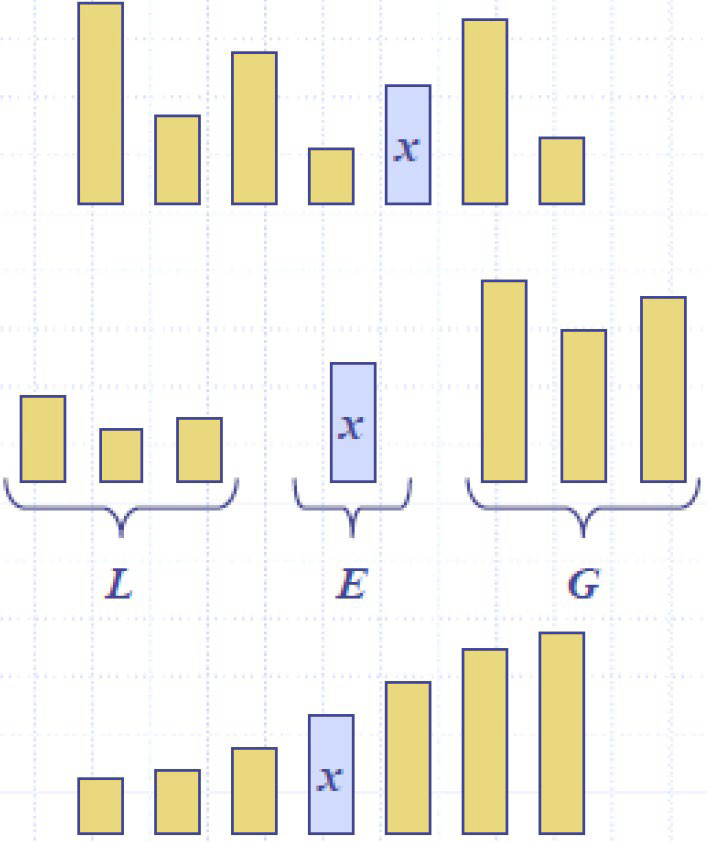
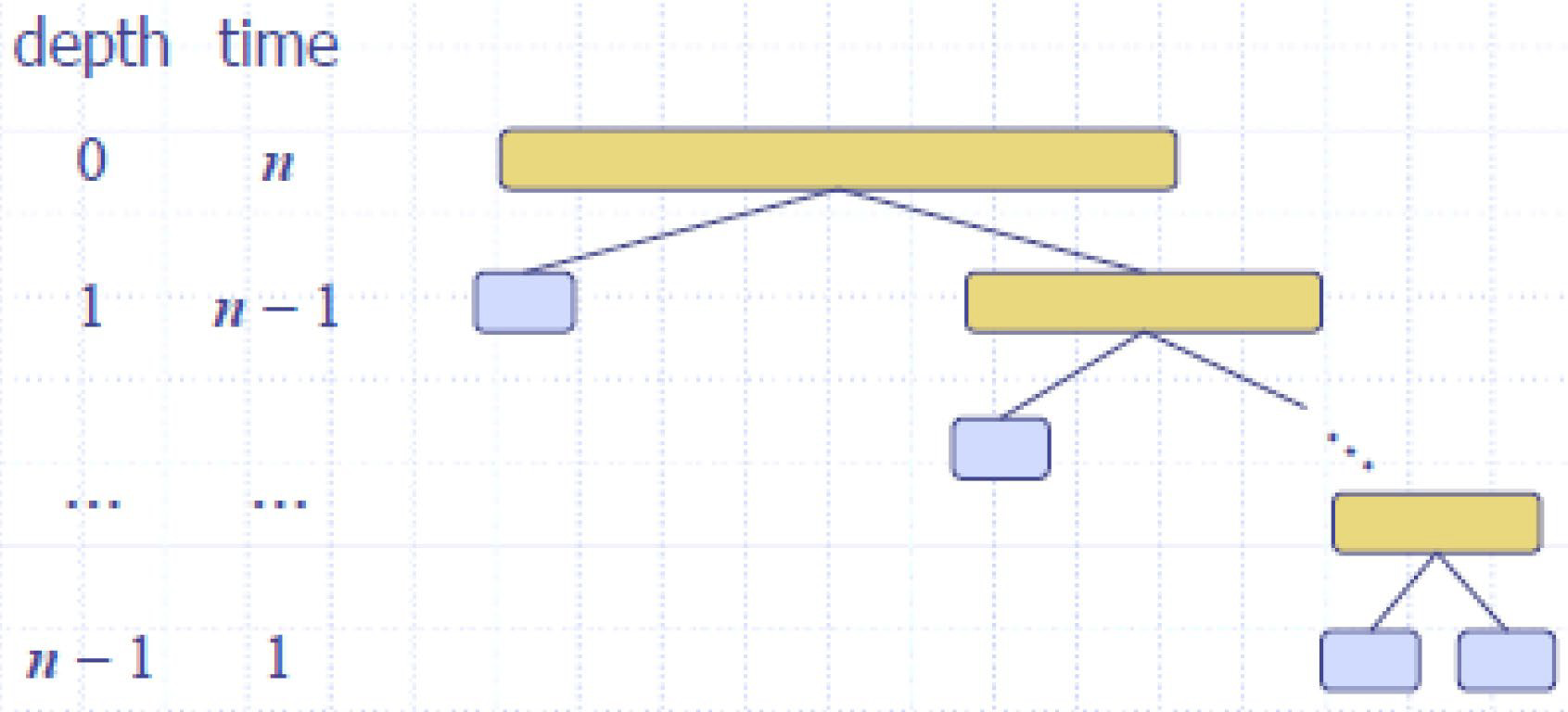
complexity
当枢轴是唯一的最小或最大元素时,会出现快速排序的最坏情况
𝐿和𝐺中一个的大小为𝑛-1,另一个的大小为0
运行时间与总和成比例
𝑛 + (𝑛𝑛 − 1) + … + 2 + 1 = O(𝑛^2)
Lec9 Complexity of Algorithms Optimization Problems
GreedyMethod
Knapsack Problem
0/1背包问题-动态规划 Knapsack_problem Dynamic Programming_哔哩哔哩_bilibili
https://alchemist-al.com/algorithms/knapsack-problem
Fractional Knapsack Problem(FKP)

IntervalScheduling
- Interval Scheduling 是一种优化问题,通常用于处理一系列时间段的安排,以最大化利用资源或满足特定的约束条件。
- 在 Interval Scheduling 中,你通常有一组区间,每个区间都有一个开始时间和一个结束时间,并且你必须选择一个最大数量的区间,使得它们之间不会相互重叠。
- 典型的例子是会议安排或资源分配问题,其中你必须选择尽可能多的会议或任务,但不能同时参加重叠的会议或同时执行重叠的任务

Task Scheduling
- Task Scheduling 通常涉及安排执行特定任务的时间表,以最大化效率或满足特定的约束条件。
- 这类问题可能更加广泛,可以涉及到各种类型的任务,例如作业调度、进程调度等。
- 在 Task Scheduling 中,任务可能有各种不同的属性,如优先级、执行时间、截止日期等。你需要设计一种算法来决定何时执行每个任务,以最大化某种指标,如完成任务的数量、满足截止日期的数量等。

Dynamic Programming
动态规划主要用于优化问题。它通常应用于暴力搜索最优值是不可行的地方。
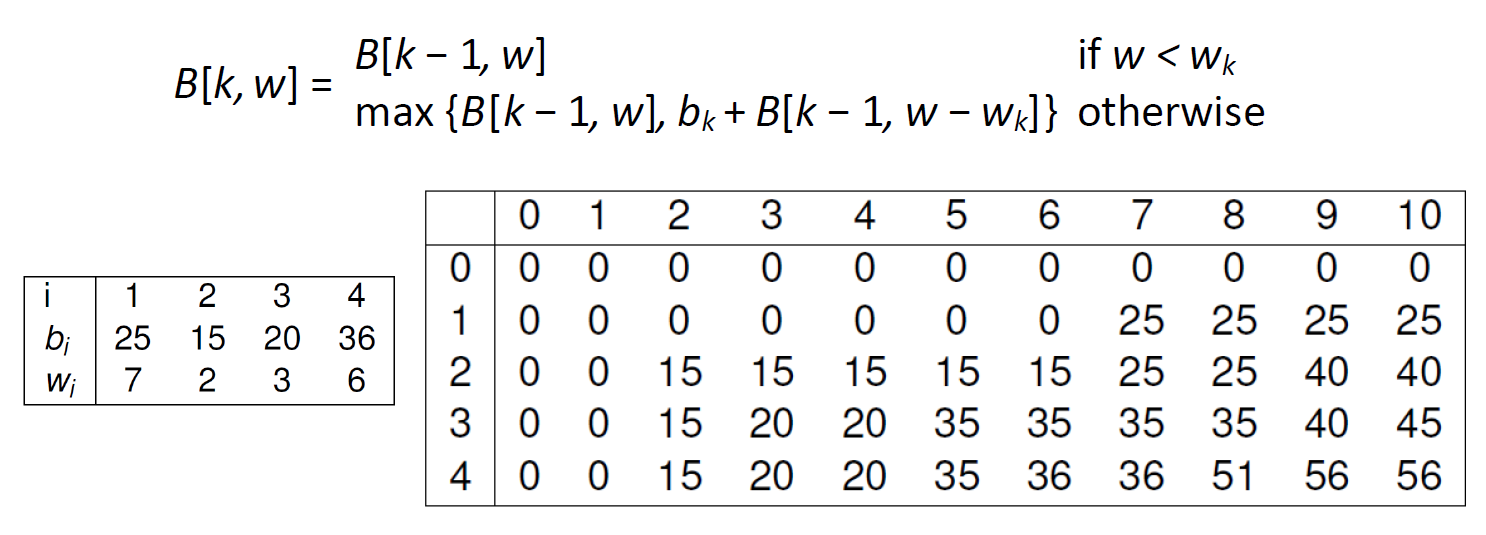
The {0 –1}KnapsackProblem
禁止携带一部分物体

Lec10 Graphs 图
A graph𝐺=𝑉,𝐸consists of a set of vertices (nodes) V and a set of edges E, where each 𝑒∈𝐸 is specified by a pair of vertices 𝑢,𝑣∈𝑉
一些术语
End vertices:一条边的顶点
Edges incident:一个顶点相邻的边
Adjacent vertices:相邻的顶点
Degree:是指一个顶点连接的边的数量
Path:交替的顶点和边的序列,从顶点开始,以顶点结尾,每条边的前面和后面都有它的sendpoints
Simple Path:所有顶点和边都不相同的路径
subgraph:子图
acyclic graph: 没有 cycle的图。树是相互连接的acyclic graph
Directed acyclic graphs 有向无环图称为dag。不可能通过遍历这些边回到同一个节点。
遍历
DFS 深度优先遍历
基本思想是我们从某个顶点开始,从这个起始顶点开始移动。在我们不得不“后退”之前,我们“尽可能走得远”,因为我们到达了一个点,在这个点上,我们遇到了之前已经找到的所有顶点。
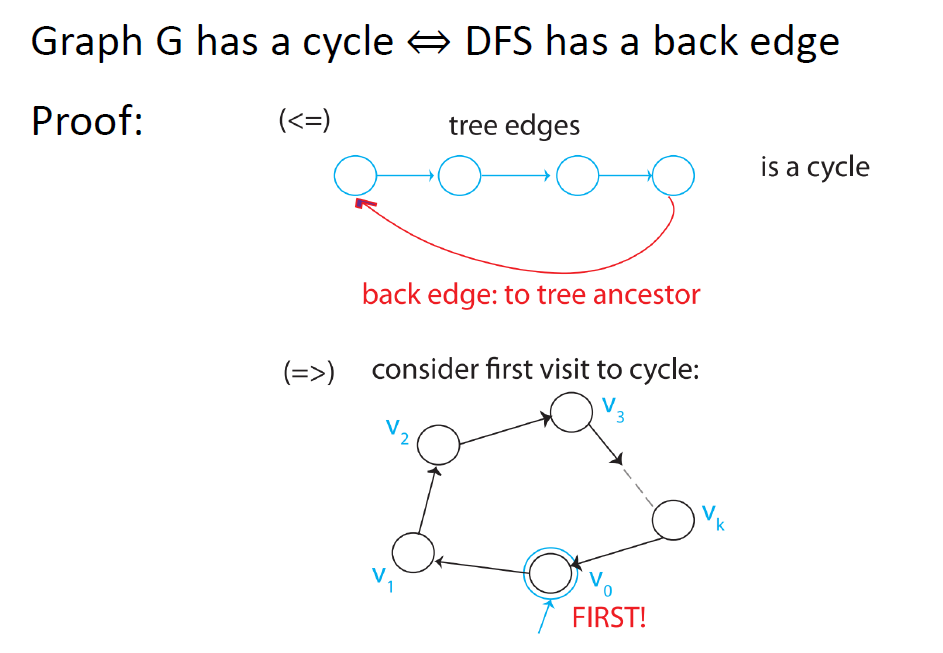
DFS:生成一棵生成树,使得所有非树边都是后边。后边:是一条(u, v)边,使得v是节点u的祖先,但不属于DFS树。这可以用于检测周期。(?)
Cycle环 检测
DFS finds topological order 找拓扑次序(?)
力扣例题
102. Binary Tree Level Order Traversal
103 Binary Tree Zigzag Level Order Traversal
1857 Largest Color Value in a Directed Graph
时间复杂度:O(V+E)
对DAG(有环无向图)中的节点进行排序,这样就没有从后面节点到前面节点的路径。

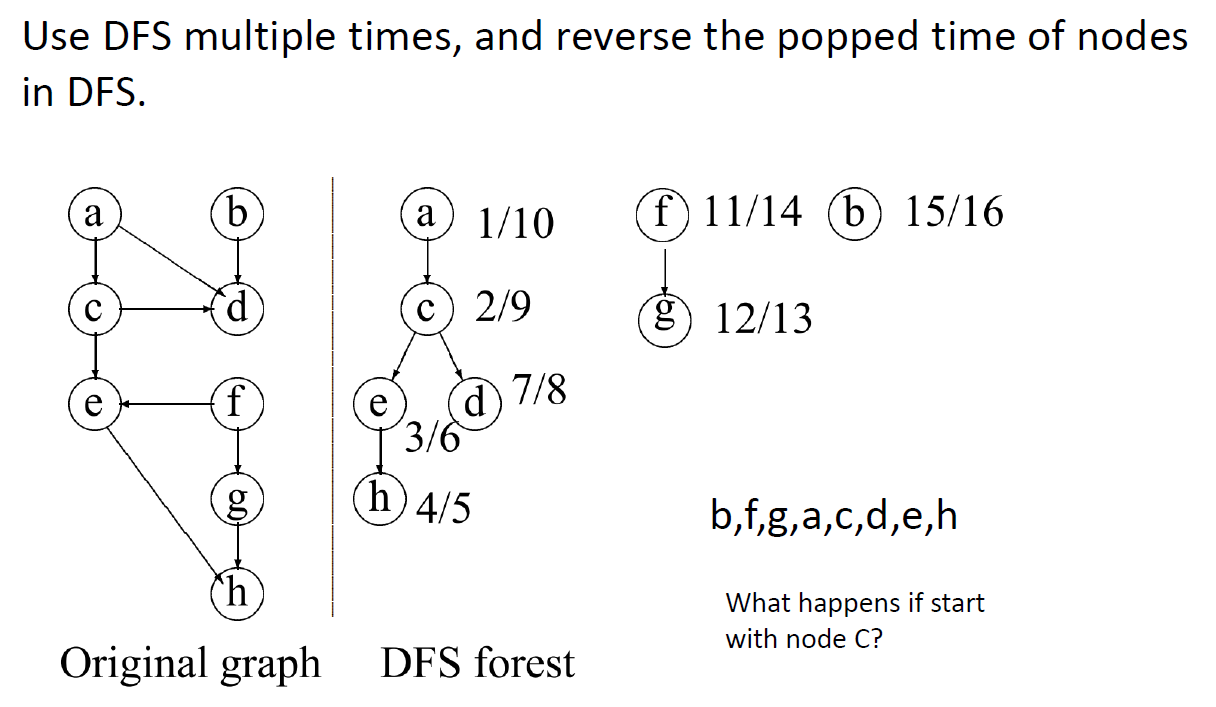
BFS 广度优先遍历
广度优先搜索算法跟踪正在探索的节点边界,然后扩展。
BFS遍历:找最短路径
Weighted Graph
加权图是一个与每条边𝑒相关联的数字标签𝑤(𝑒)的图,称为𝑒的权重。
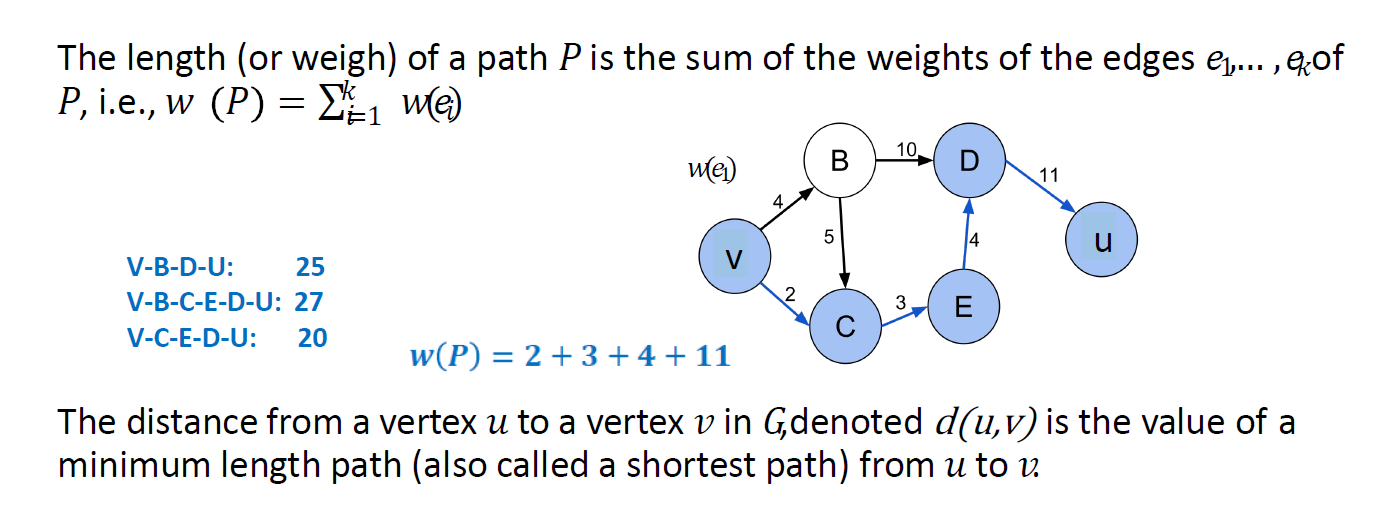
single source shortest path 单源最短路径
对于某个固定顶点𝑣,从𝑣找到所有其他顶点𝑢≠𝑣在𝐺的最短路径(将边的权值视为距离)
Greedy Approach
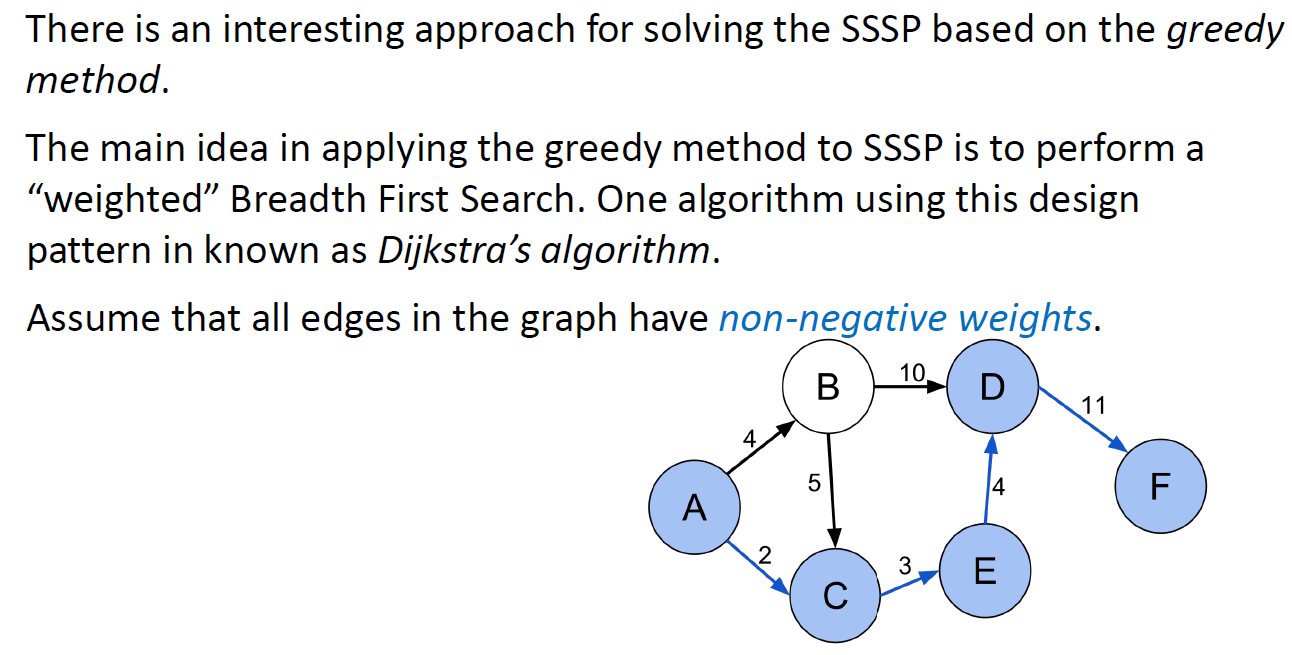
Dijkstra


定理 Lemma
1.

2.
![]()
时间复杂度 O(VlgV +ElgV)

Bellman-Ford O(VE)
Dijkstra 无法处理负权边的问题,但是Bellman-Ford可以解决
 Minimum Spanning Tree (MST) 最小生成树
Minimum Spanning Tree (MST) 最小生成树
设G是一个无向图。我们也经常感兴趣的是找到一个生成树T,即G的一个无环生成子图,它使T的边权之和最小。这样的树就是最小生成树,简称MST。
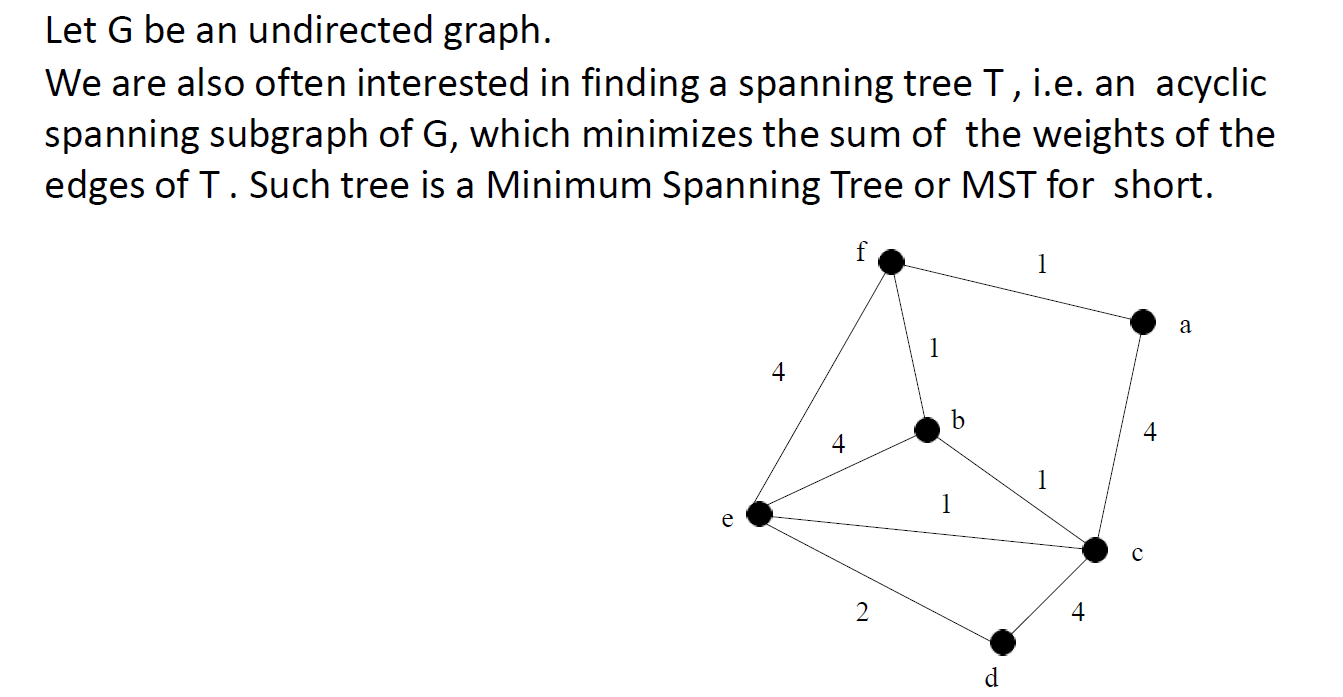
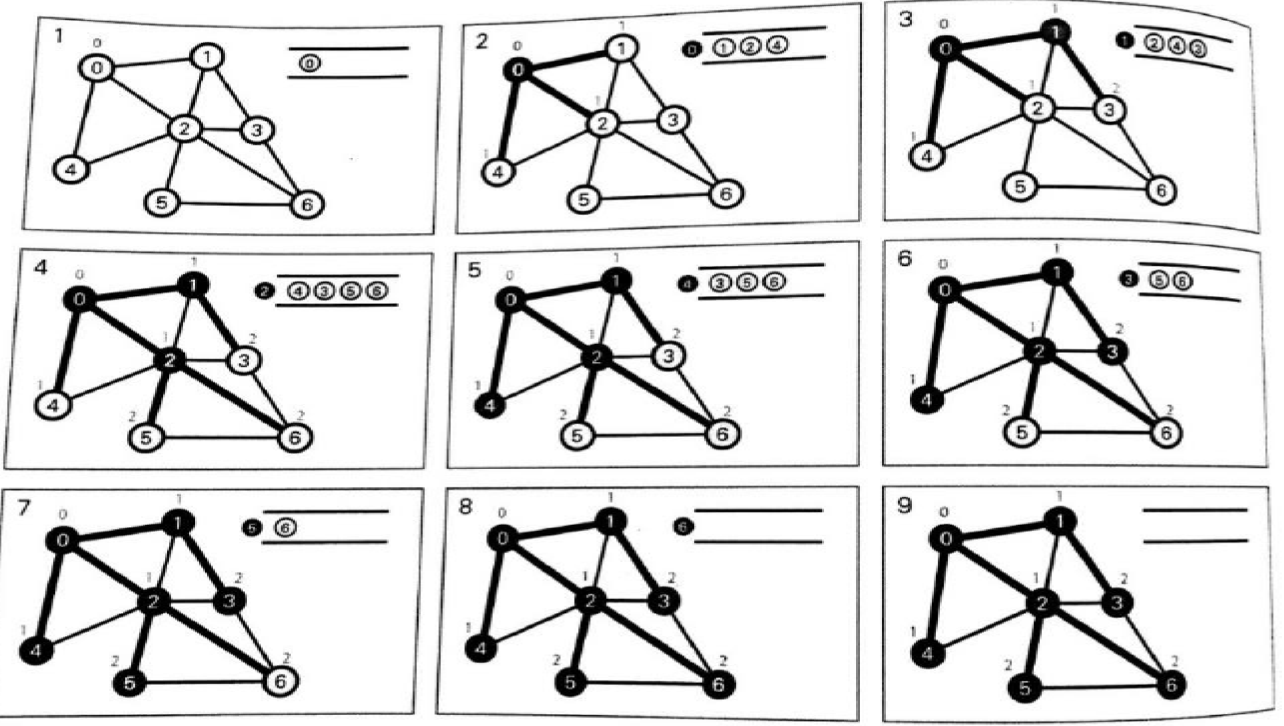
Prim’s algorithm
finds MST by greedy expansion of the tree

Kruskal’s Algorithm
finds MST by greedy selection of cheap edges globally
787. Cheapest Flights Within K Stops
. - 力扣(LeetCode)
1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

Union-Find
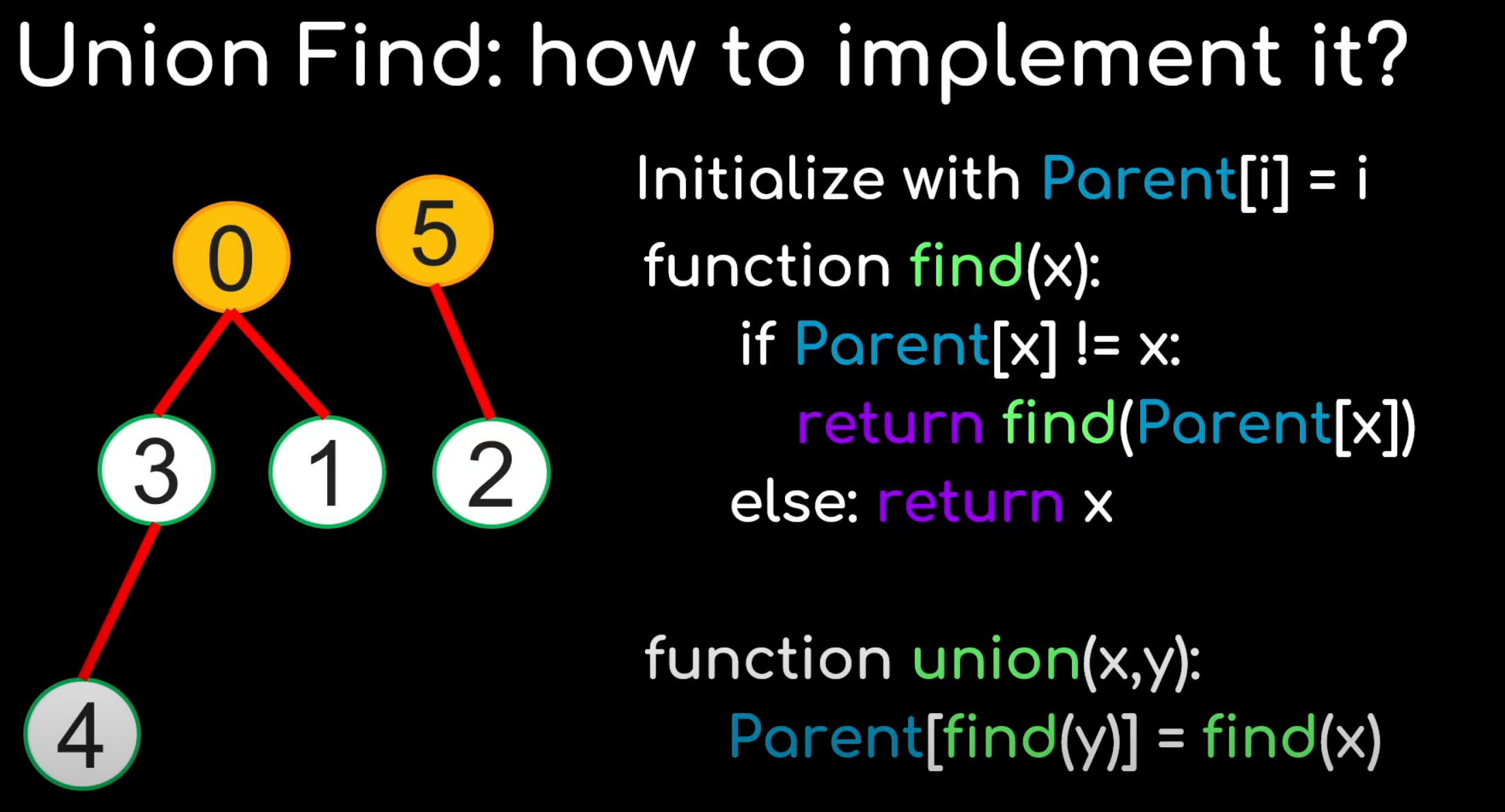
L11 Flow
这节可以直接参考视频13-1: 网络流问题基础 Network Flow Problems_哔哩哔哩_bilibili
Flow 流量
流量是从源节点流向汇节点的量,必须满足容量限制和流量守恒原则(即每个中间节点的流入流量等于流出流量)。
- 容量限制:每条边上的流量不能超过该边的容量。
- 流量守恒:除源节点和汇节点外,每个节点的流入流量必须等于流出流量。
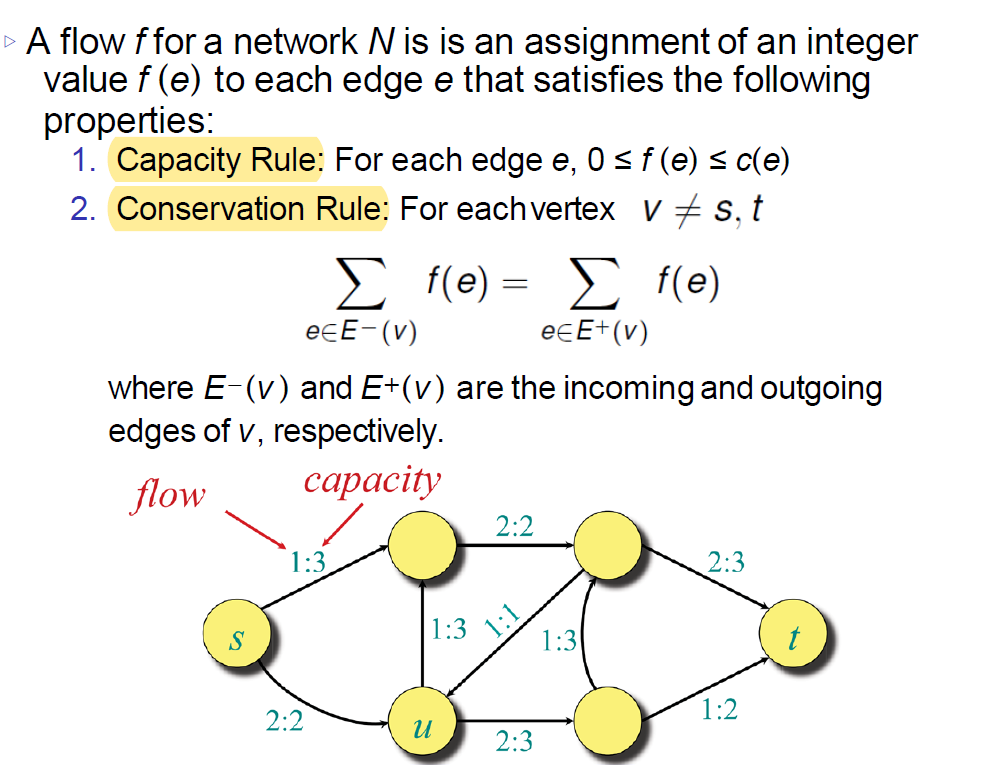

Flow Network
网络流问题 是图论中的一个经典问题,涉及在一个有向图中从源节点(source)到汇节点(sink)的流动。以下是一些关键概念
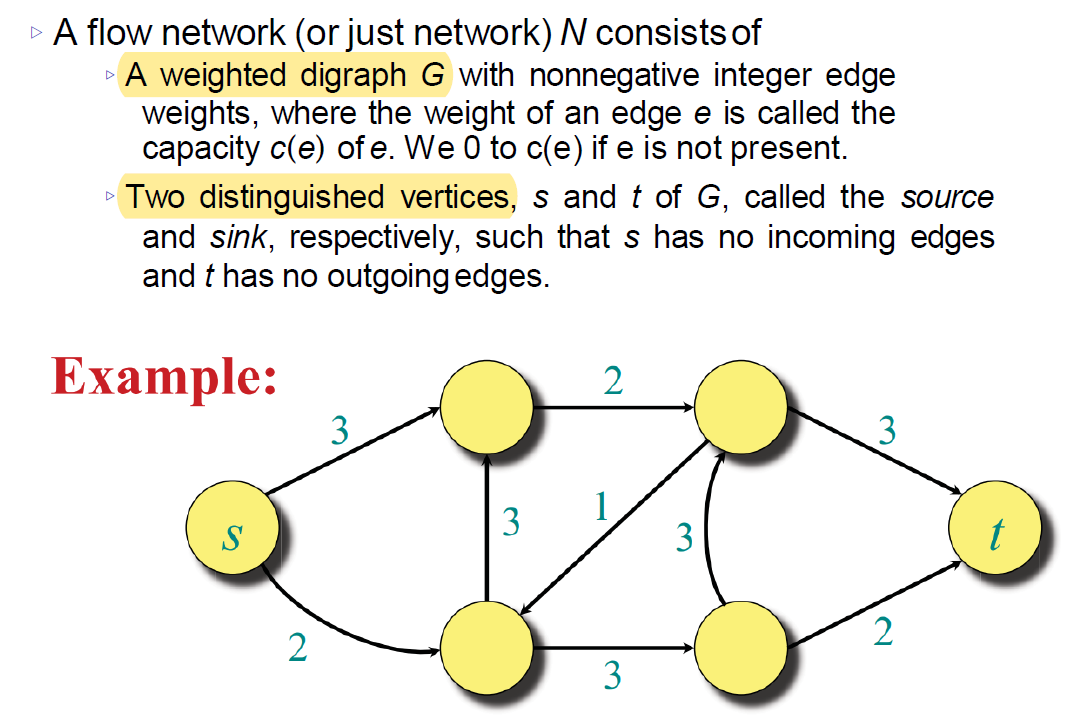
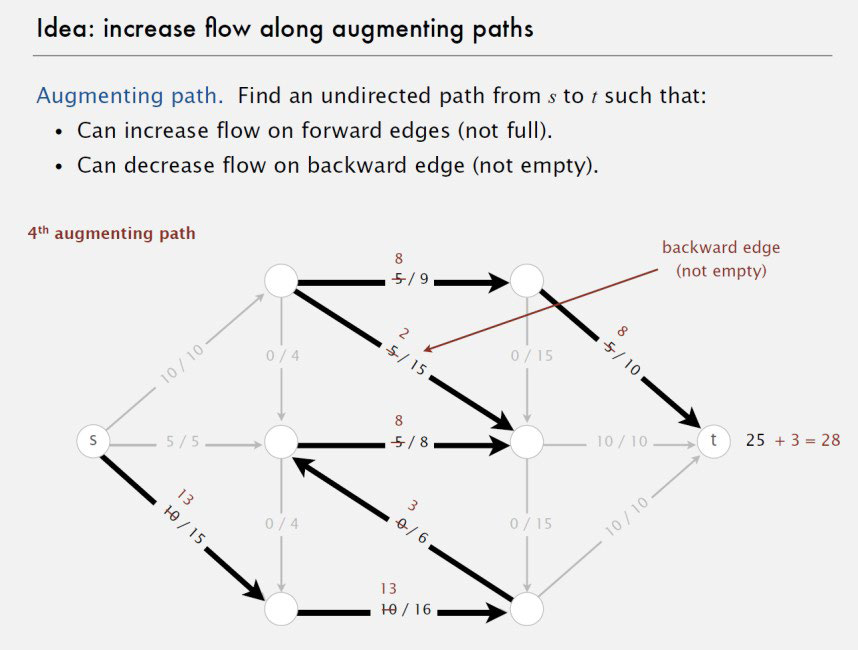
Augmenting Path and Residual Network
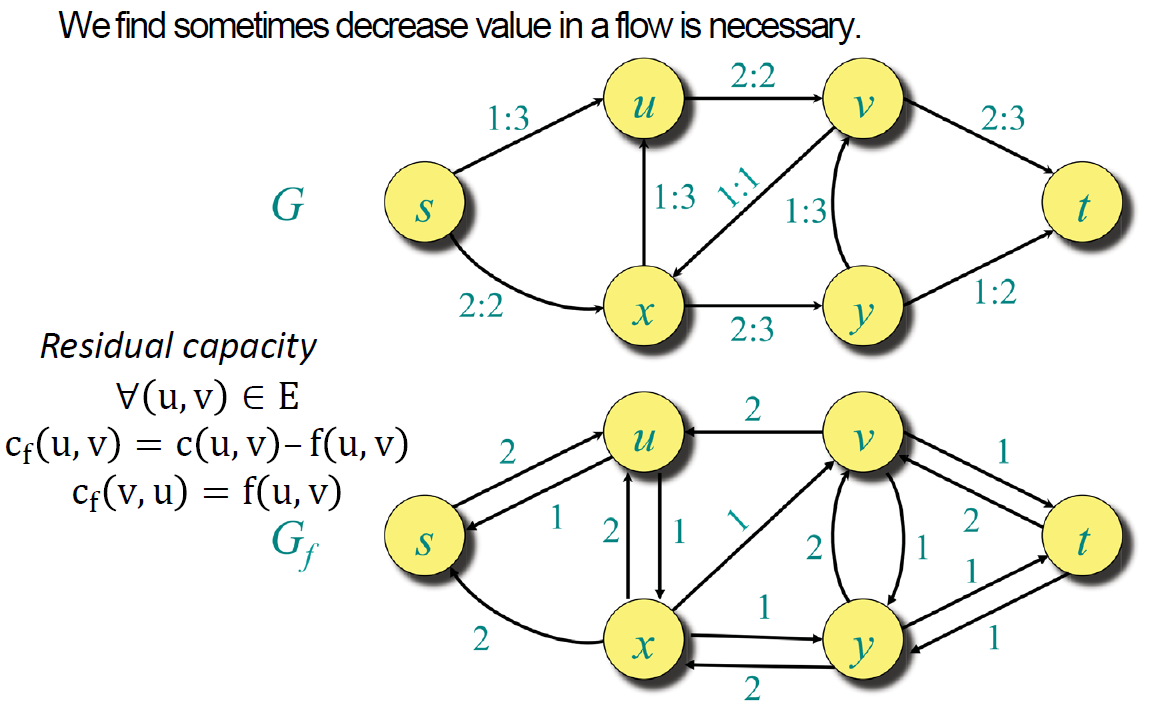
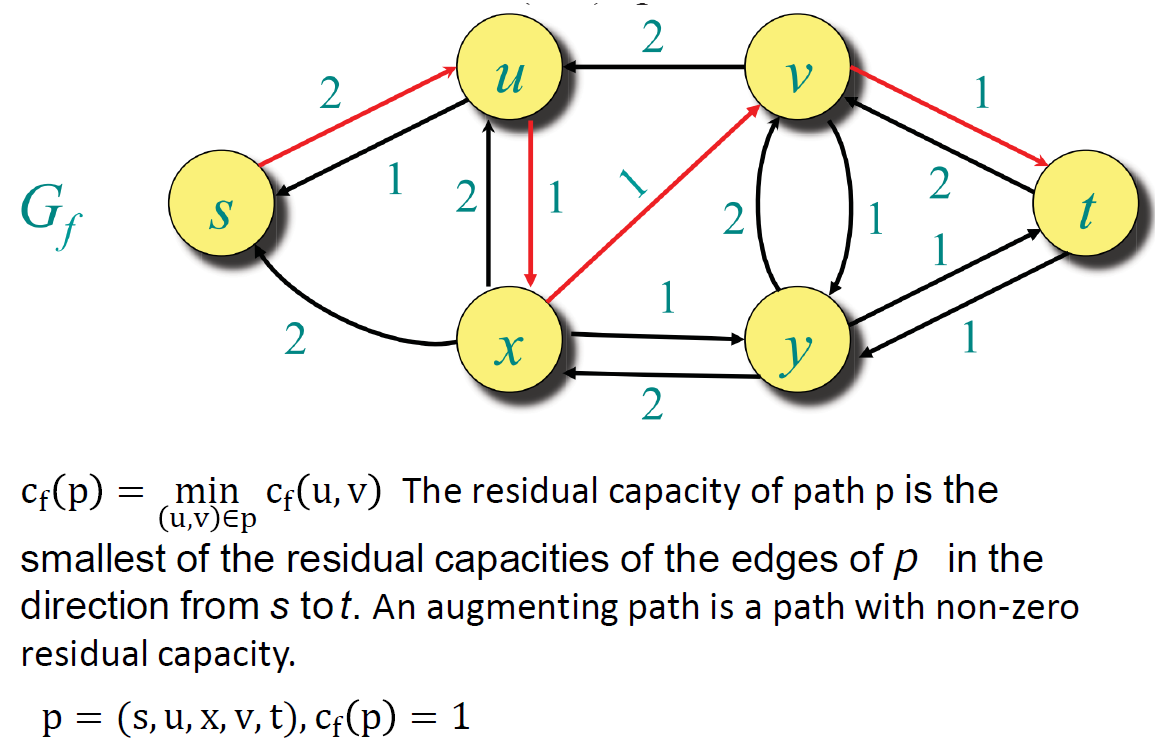
Maximum Flow 最大流
最大流问题可以理解为一个水管每秒最多能输送多少立方米的水到终点


简单解法(不能保证最优性)
先找augmenting path(起点s到终点t的简单路径(最短),不能有回路),然后算残余量,饱和了的边就去掉,完成一轮循环

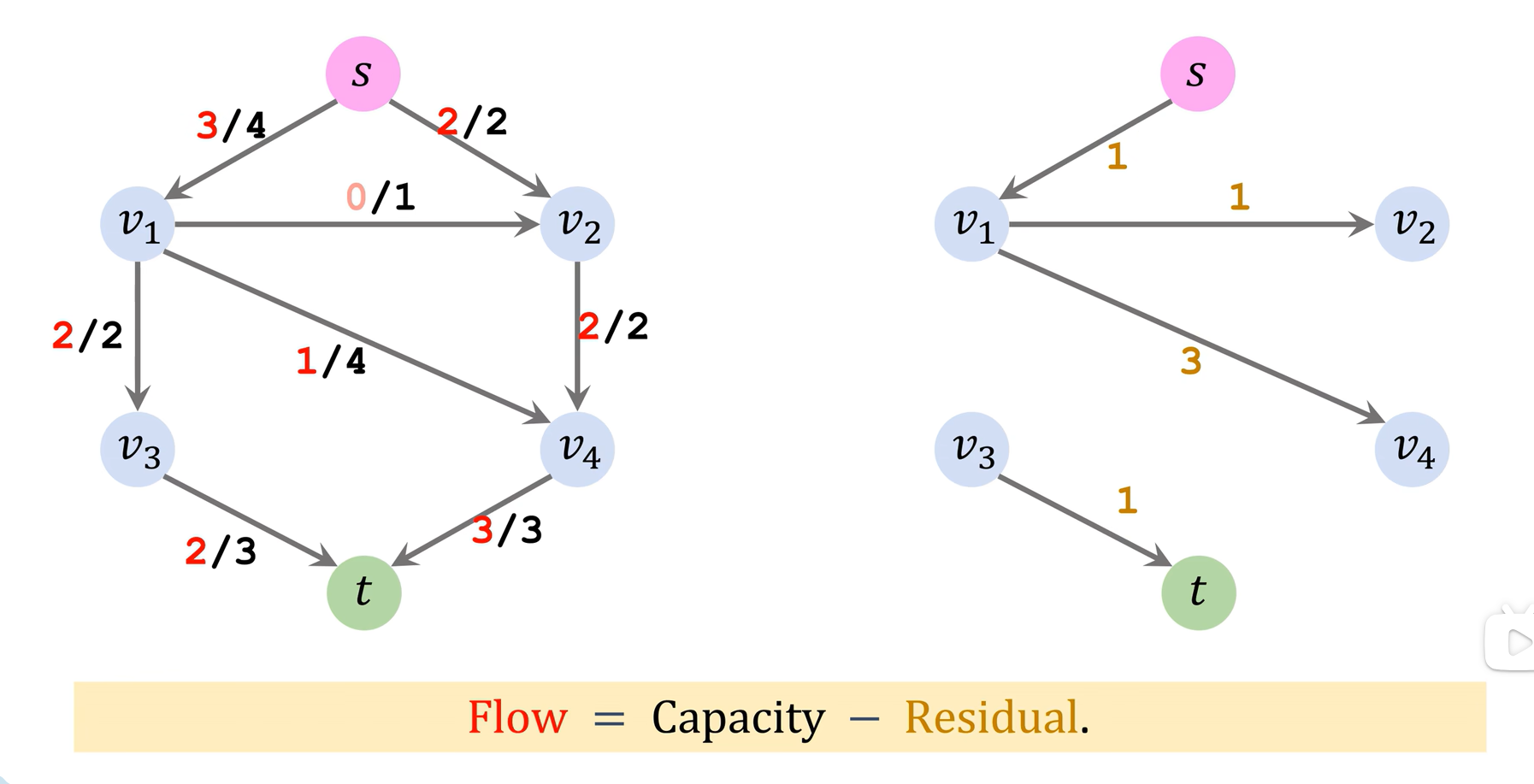
这种方法只能找到阻塞流,不一定是最大流。算法不会反悔,不能纠正错误
Ford-Fulkerson Algorithm
1.先找到augmenting path
2. 添加backward path


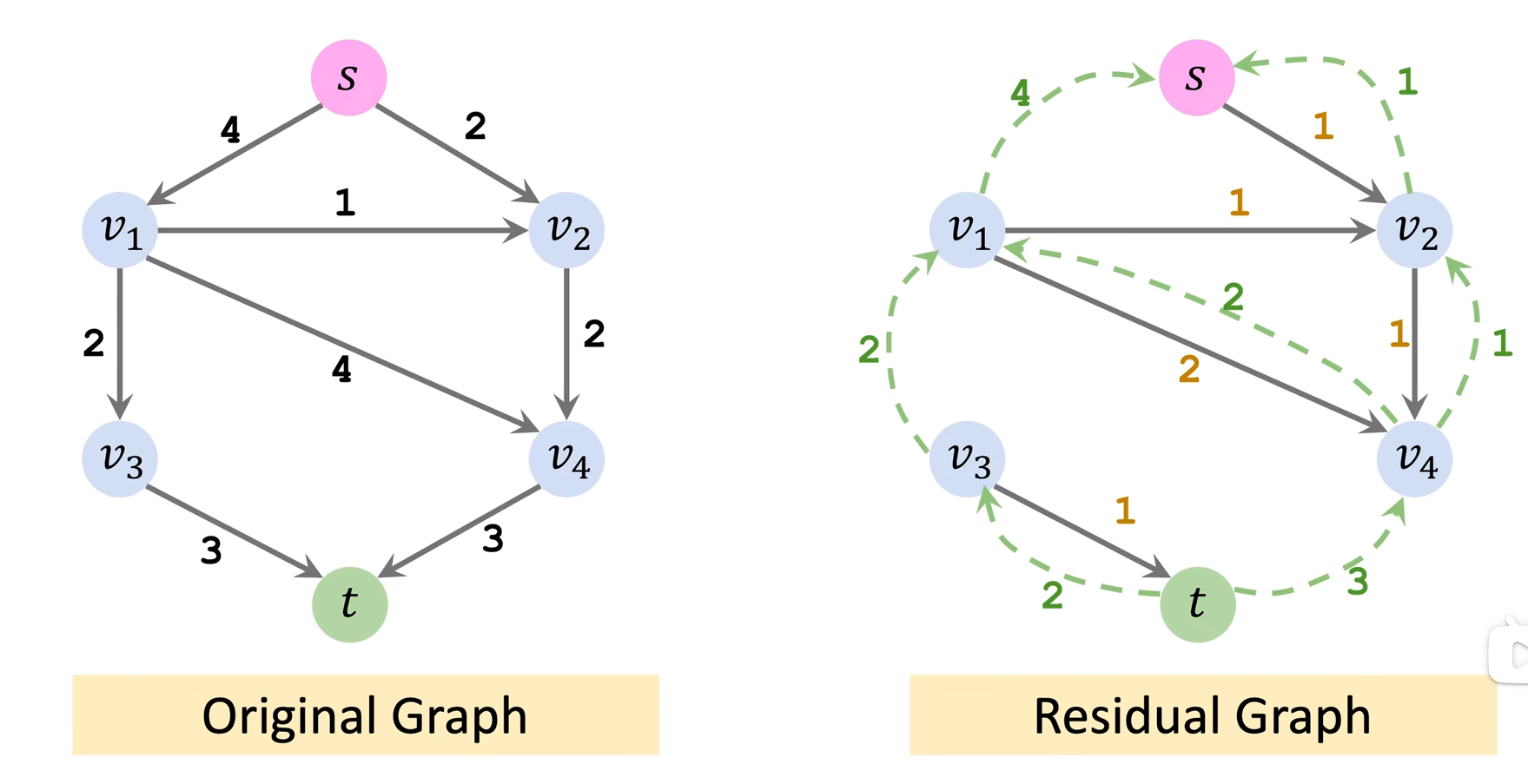
缺点:是很慢的算法

优化:Edmonds-Karp:把图当成无权图


Min-Cut 最小割
Cut
割是将一个图分成两部分的操作,具体来说,是将所有从源节点到汇节点的路径断开。一个割可以用两个节点集合表示:
- 集合 S:包含源节点。
- 集合 T:包含汇节点。
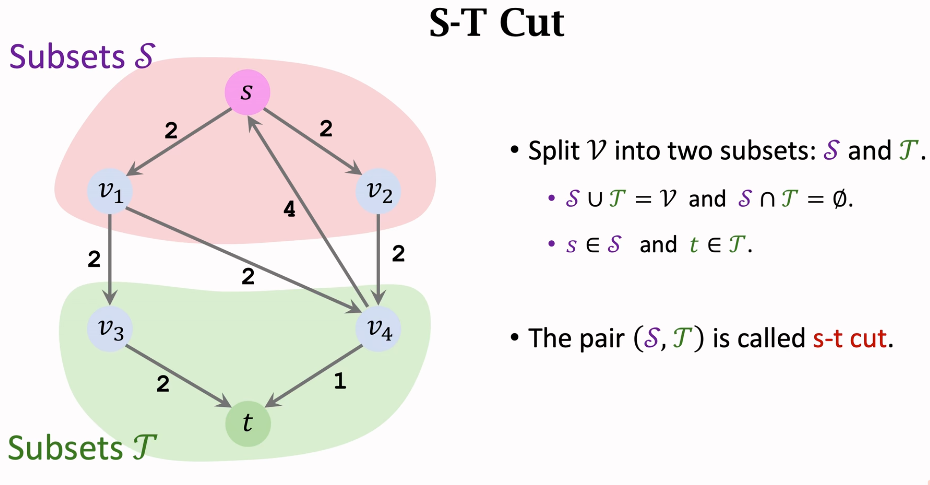
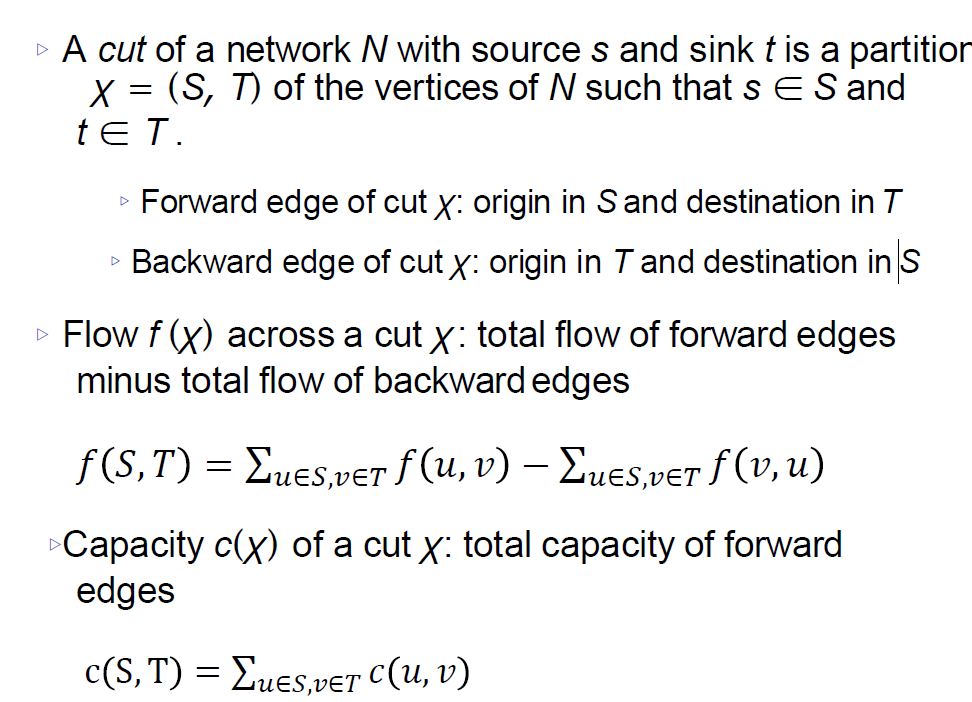
割的容量是从集合 S 到集合 T 的所有边的容量之和,即这些边的容量总和表示如果把这些边完全切断,最多可以阻止多少流量。
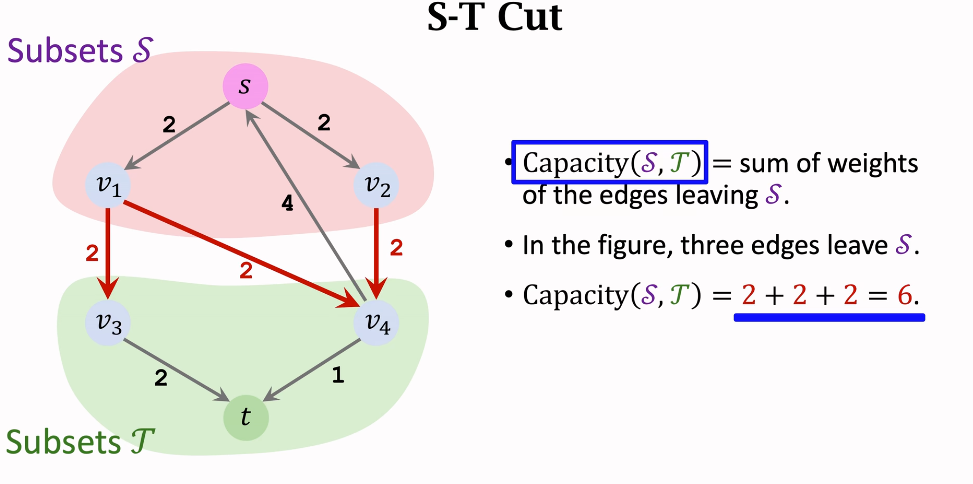
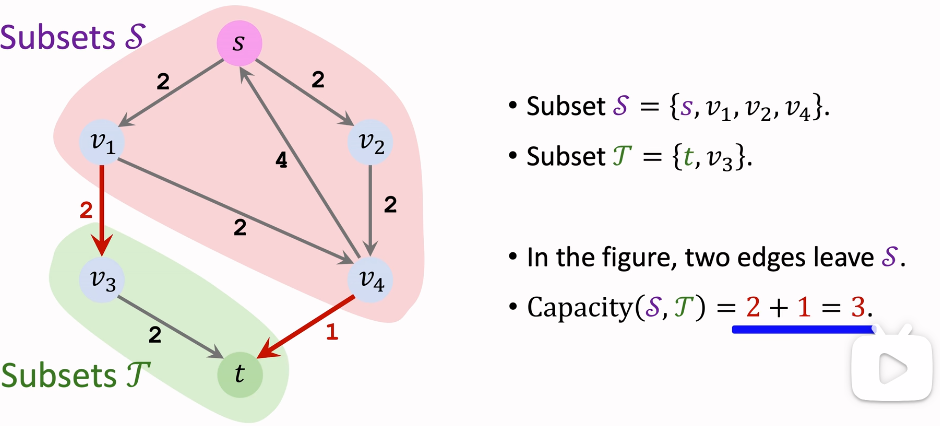
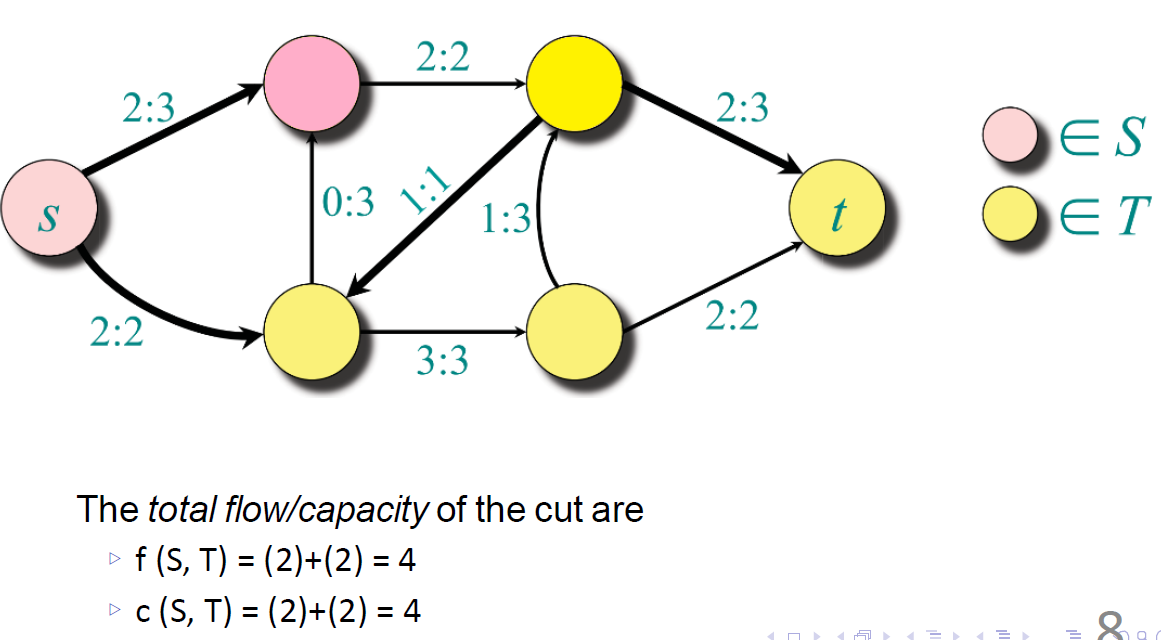
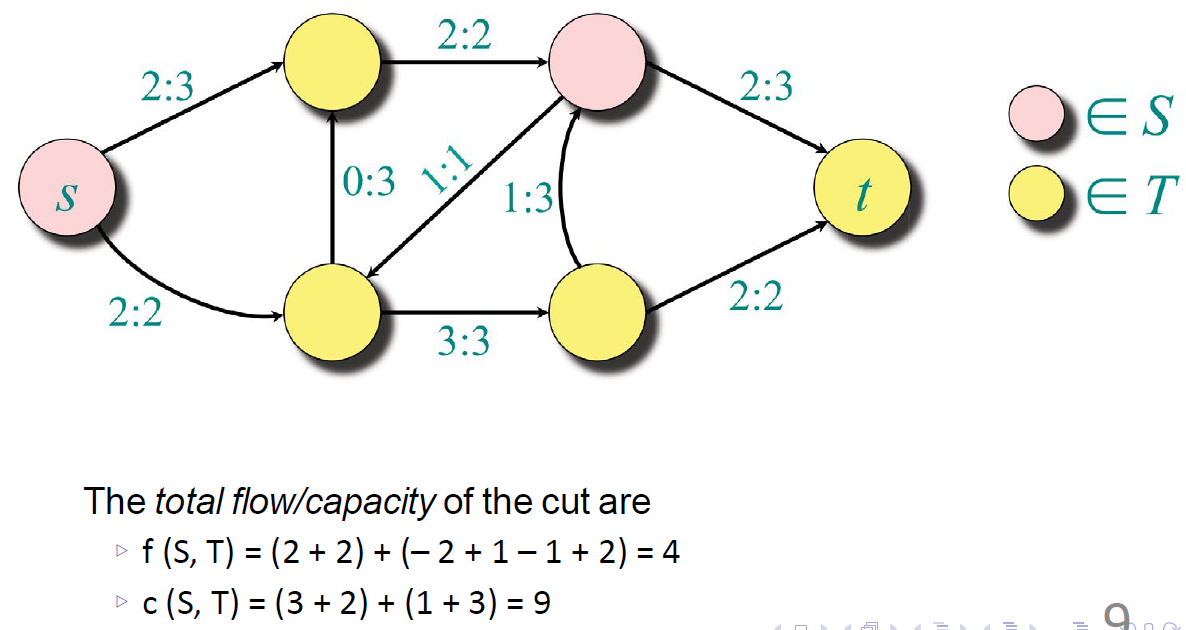

Flow & Cut

定理1

定理2

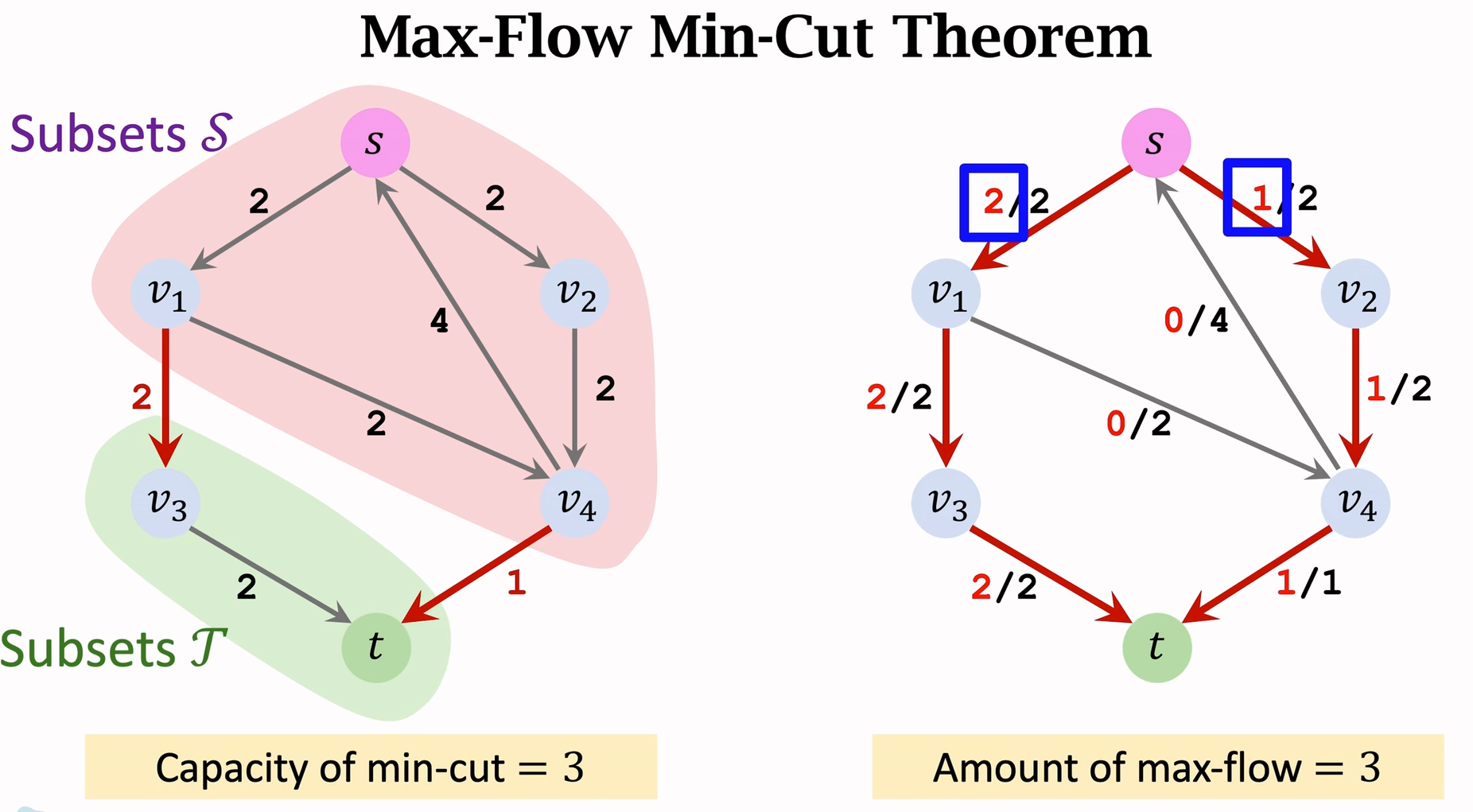
Max-flow, min-cut theorem
Leetcode1349. Maximum Students Taking Exam
最大流的流量等于最小割的容量

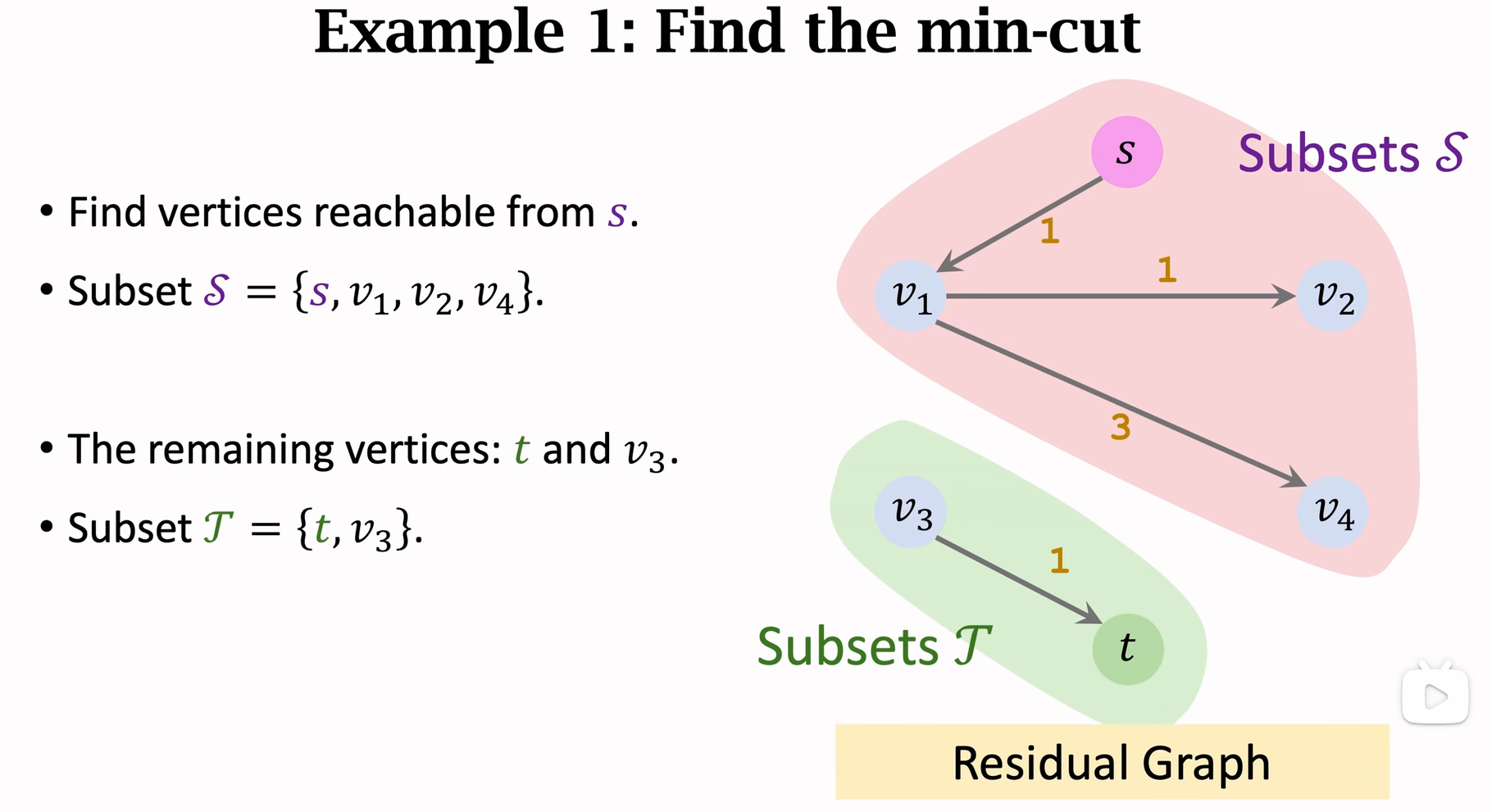
那如何找最小割呢


Match
参考视频14-1: 二部图及其判定算法 Bipartite Graphs_哔哩哔哩_bilibili
这条命全是这个up给的
Leetcode
Leetcode 2410. Maximum Matching of Players With Trainers
Leetcode 1349. Maximum Students Taking Exam
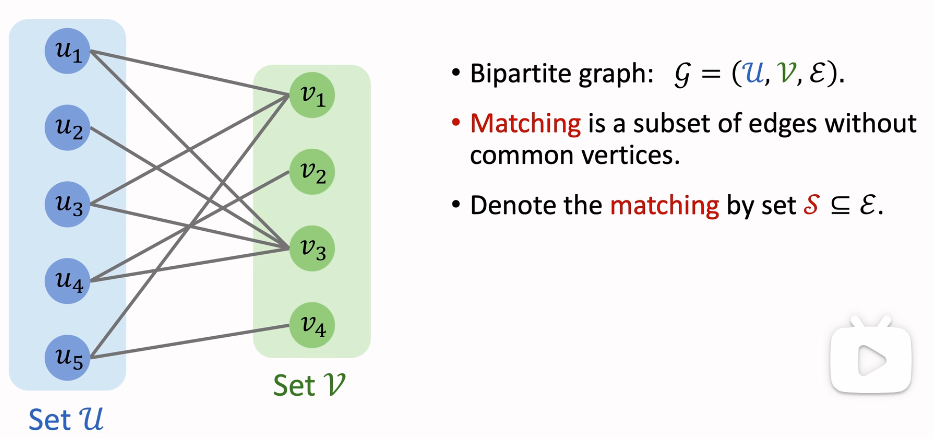
bipartite Graph 二部图

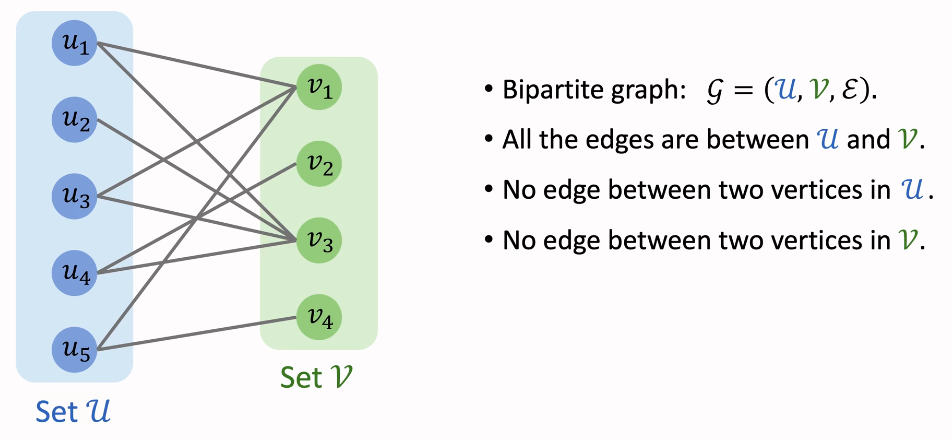
匹配
e.g 匹配程序员岗位,相亲等

二部性判断



e.g1 符合

e.g2 不符合
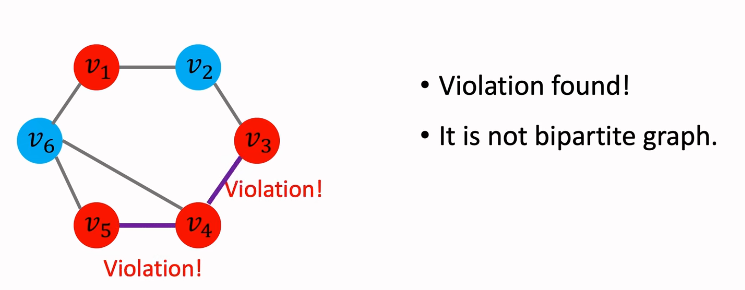
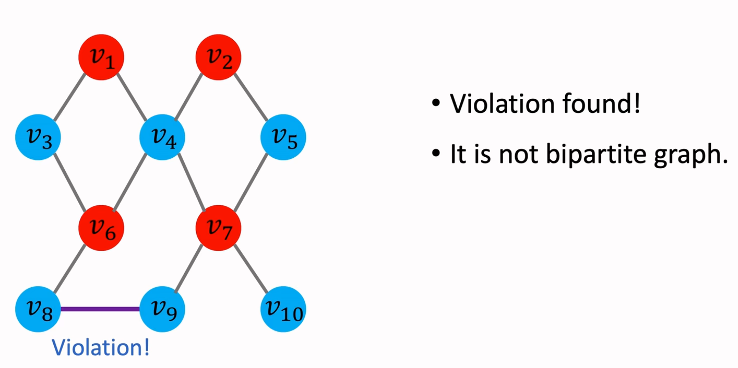
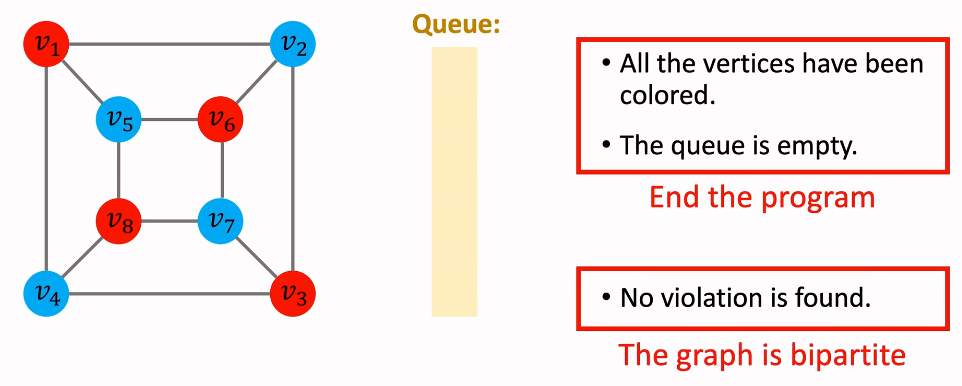
Maximum Bipartite Matching 最大匹配
所有匹配中边最大的


如果没有暴露顶点,则匹配是完美的。匹配不一定是唯一的。
解法
贪心算法并不能好好解决这个问题,所以最好把最大匹配问题转化成最大流问题
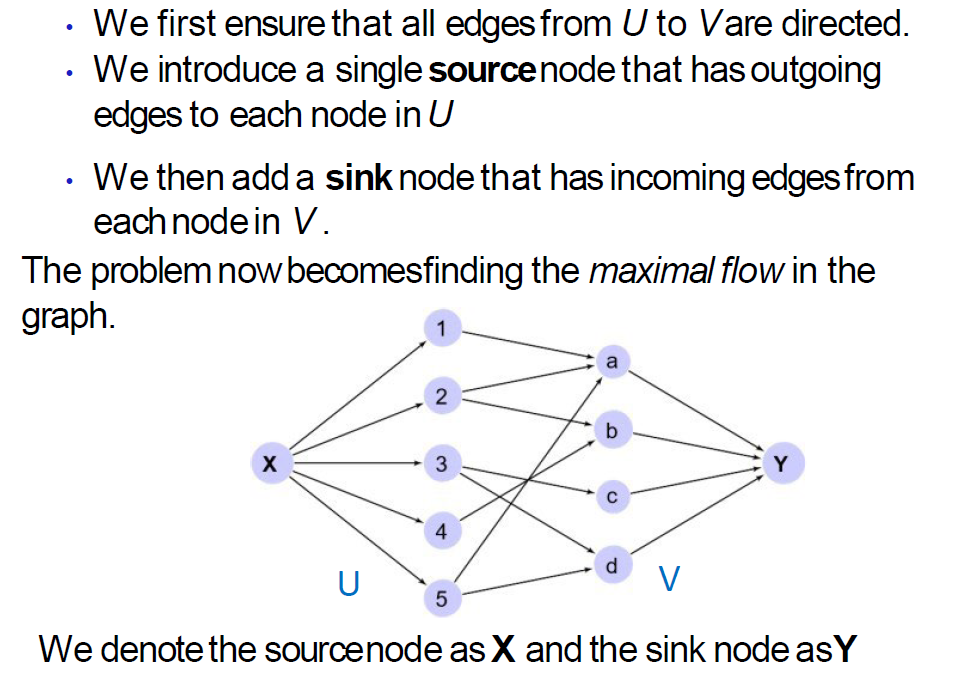

无权



用网络流问题解决匹配问题
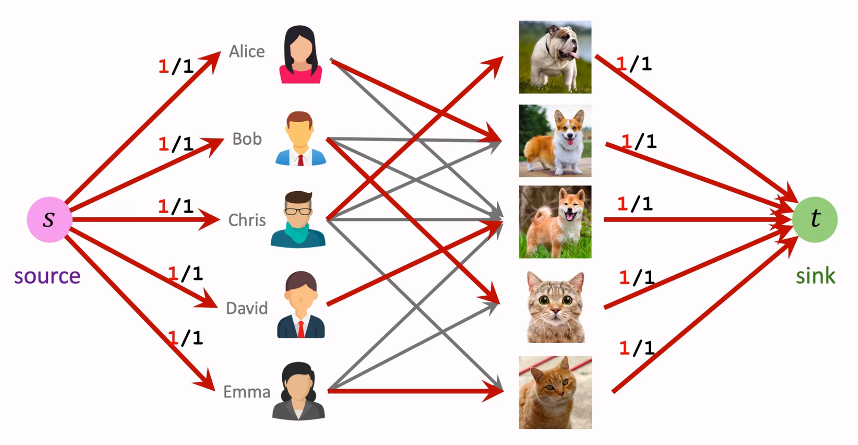
L13 Modular Arithmetic
Symmetric Cryptography 对称加密
e.g Alice &Bob

One-time pad
一次性密码本(One-Time Pad,简称OTP)是一种理论上无法破解的加密方法。它的安全性基于一个关键前提:加密和解密使用的密钥必须完全随机、至少与消息一样长,并且只能使用一次。
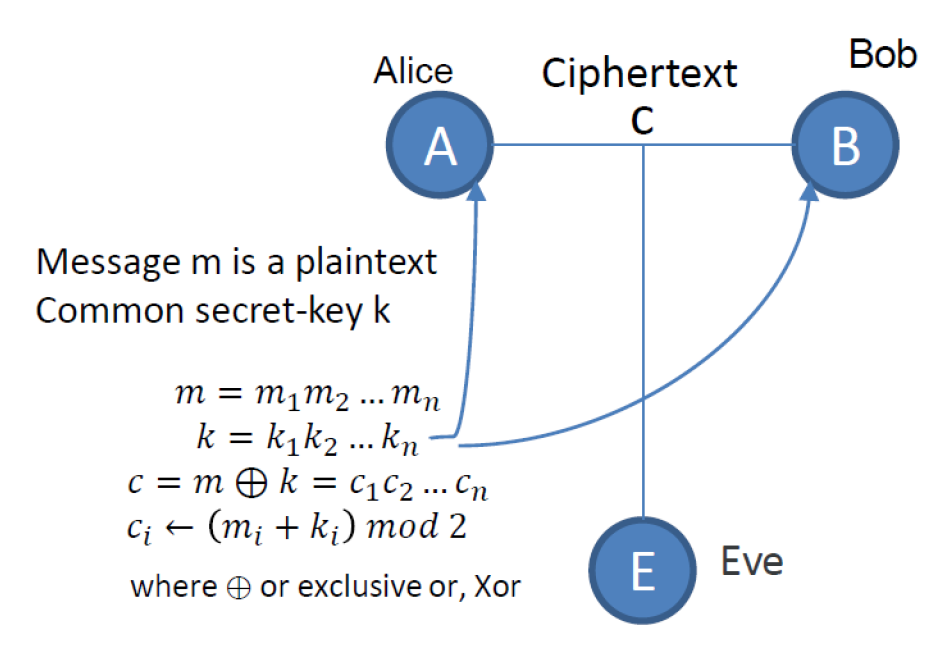
优缺点

Public Key
cryptosystem


Modular Arithmetic
Multiplication and Inverse

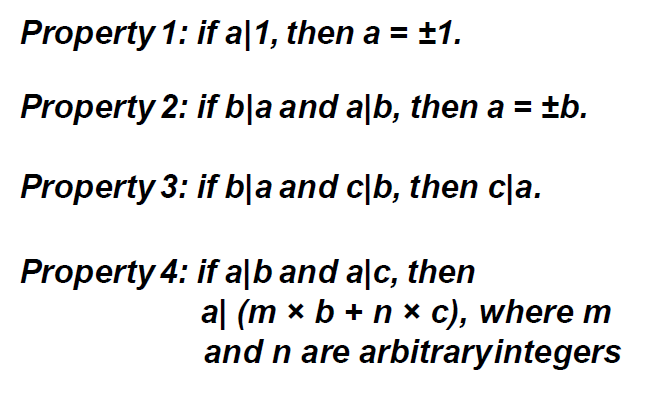

Extended Euclidean algorithm
basic
欧几里得算法(Euclidean Algorithm)是一个用于计算两个非负整数的最大公约数(GCD,Greatest Common Divisor)的高效方法。最大公约数是能整除这两个整数的最大整数。欧几里得算法基于以下重要的数学性质:两个整数的最大公约数等于其中较小的整数与两数相除余数的最大公约数。

当gcd (a, b) = 1时,我们说a和b是相对素数
用图像解释就是
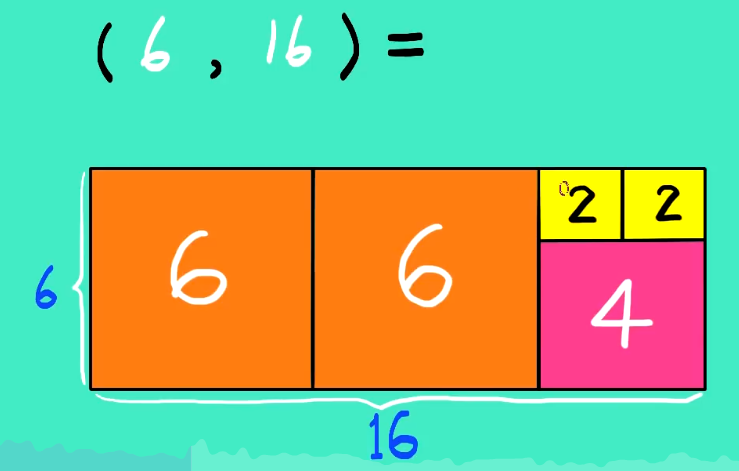
原理
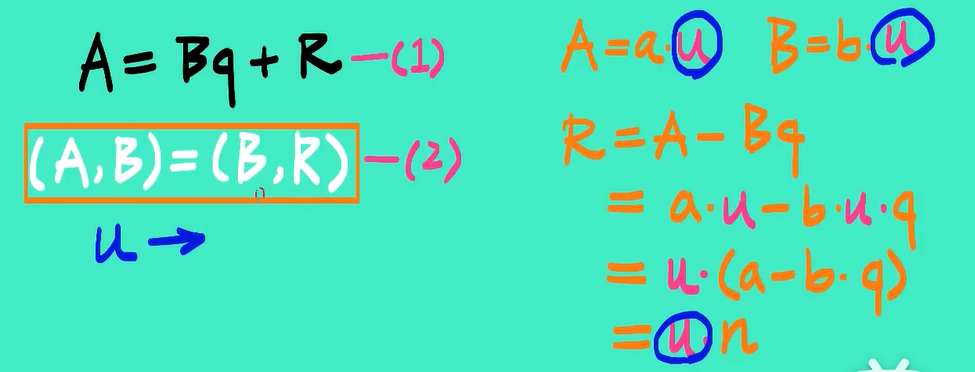
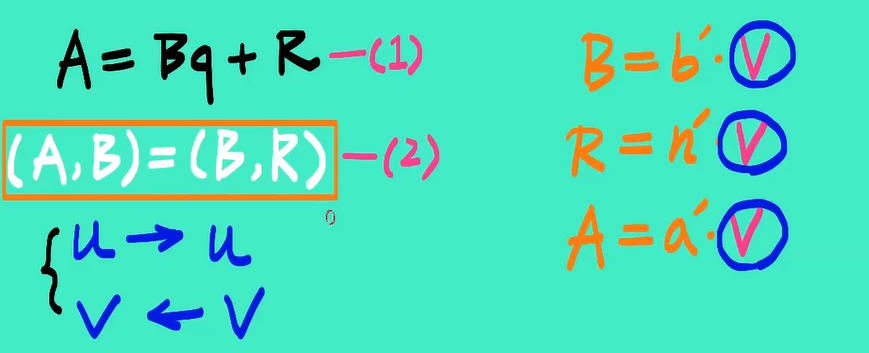
e.g
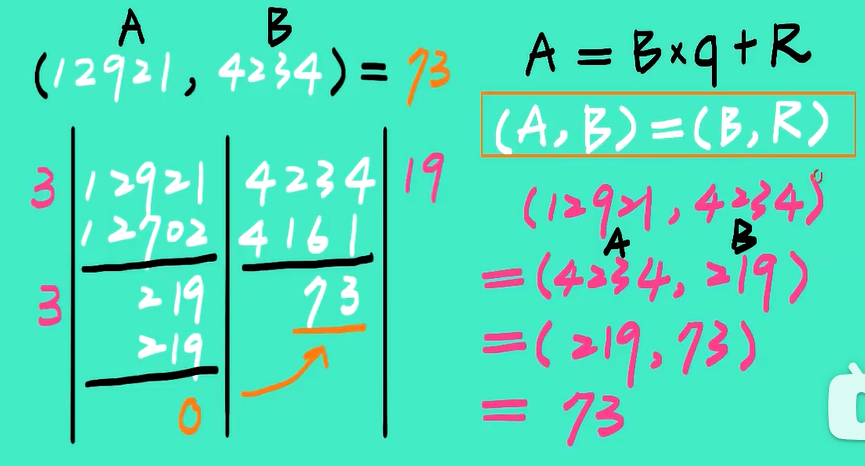
e.g3

Extended

e.g1

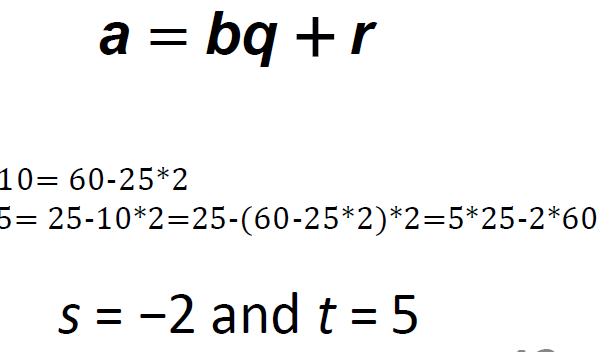
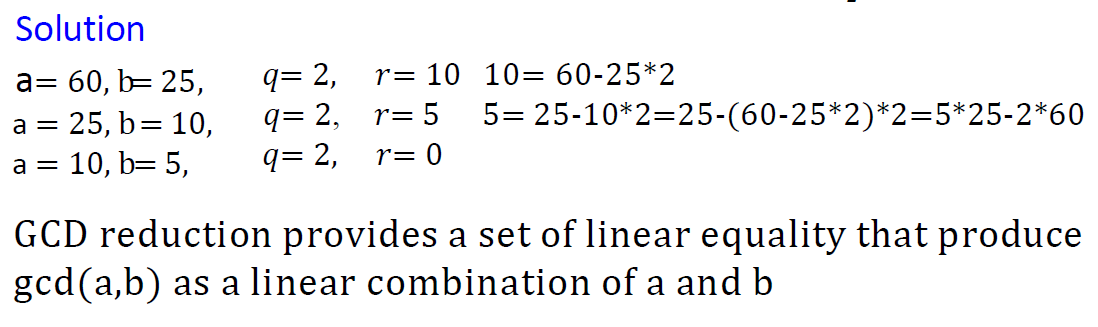
e.g2
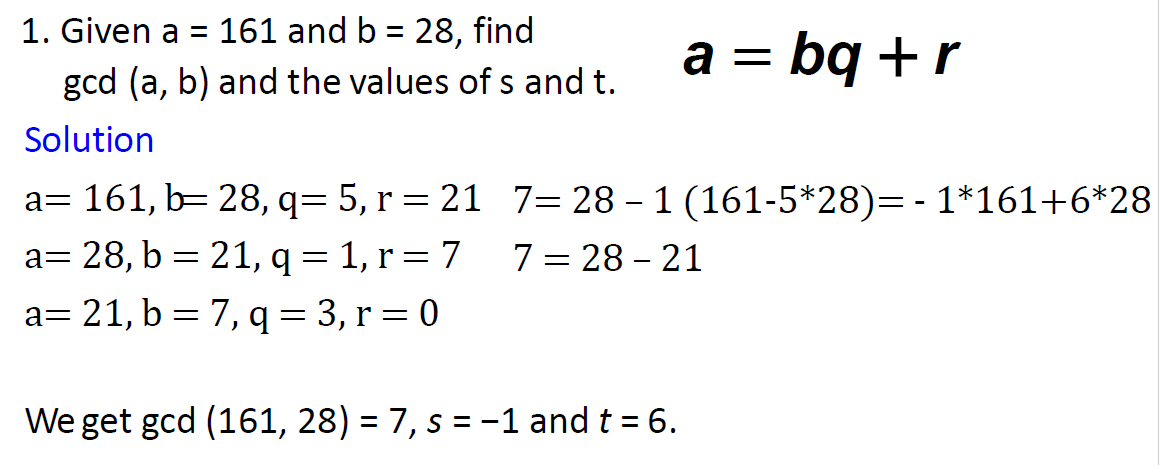
e.g3

Fast Modular Exponential
学的最痛苦的一节,还好下学期选课没选密码学
Modulo Operator 朴实无华模运算

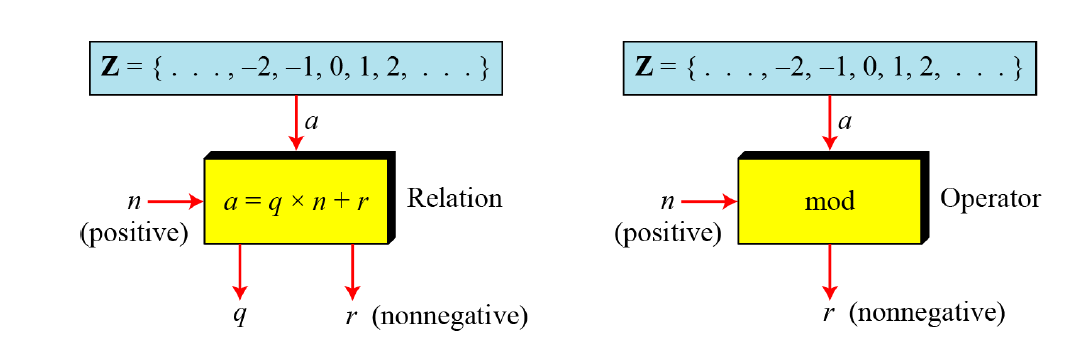
Set of Residues

congruence 同余

注意!

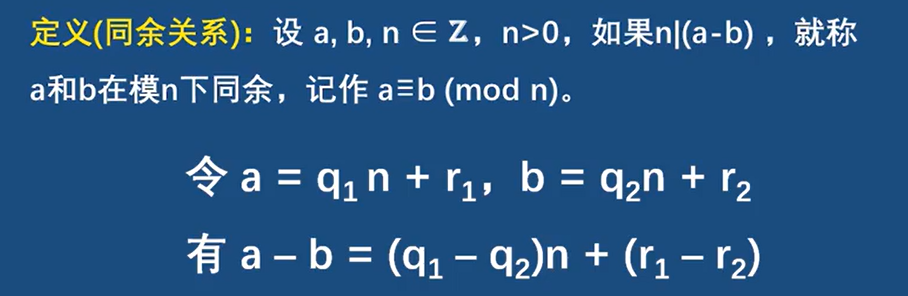
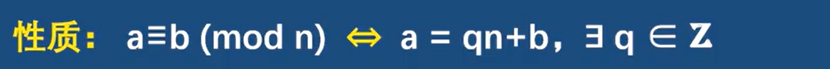
*同余是一个的等价关系,具有自反性,对称性和传递性
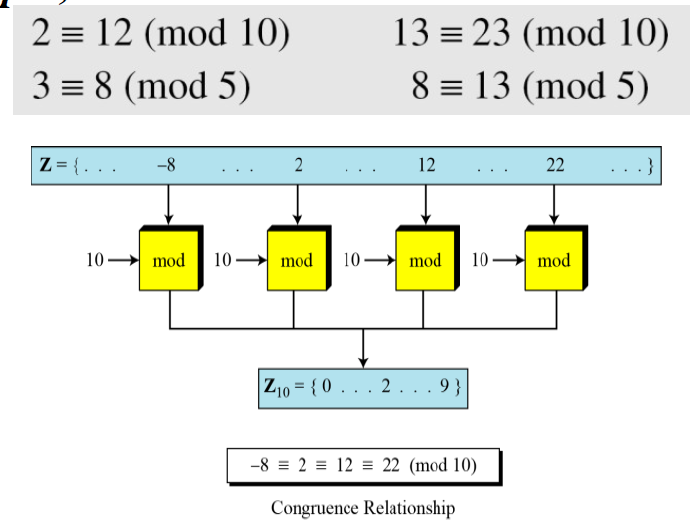
residual class 剩余类



Operation in Zn
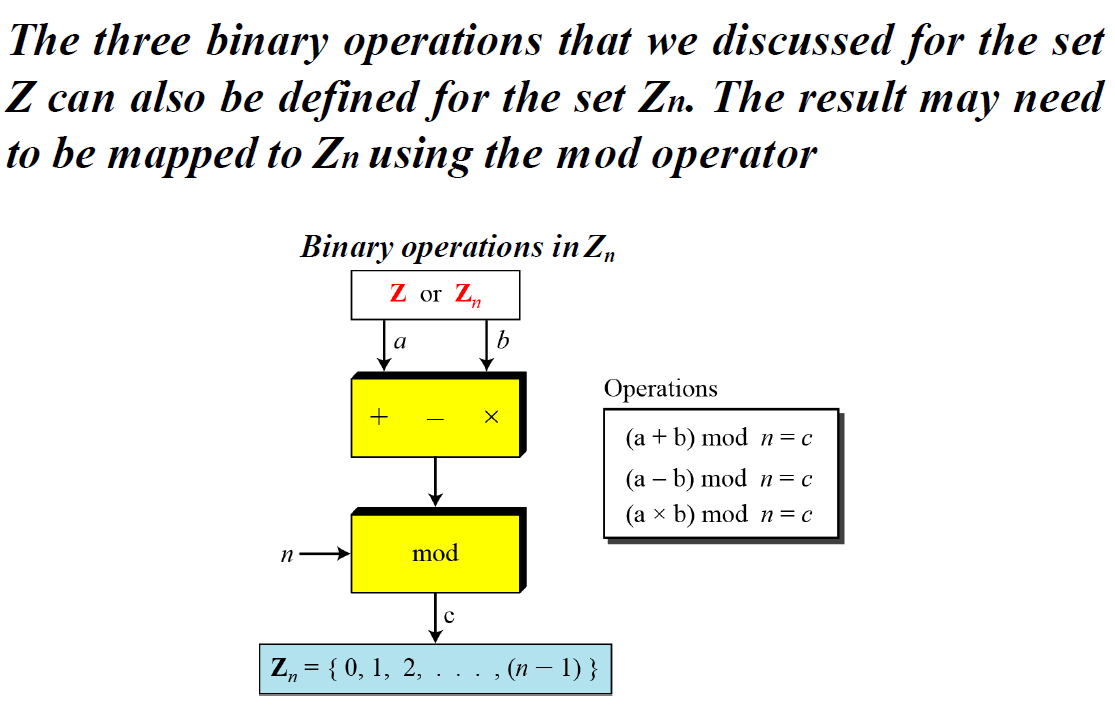
模运算的性质


e.g1
性质1
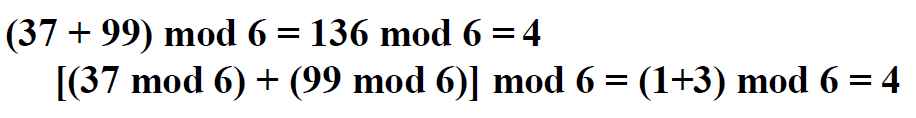
e.g2
性质4
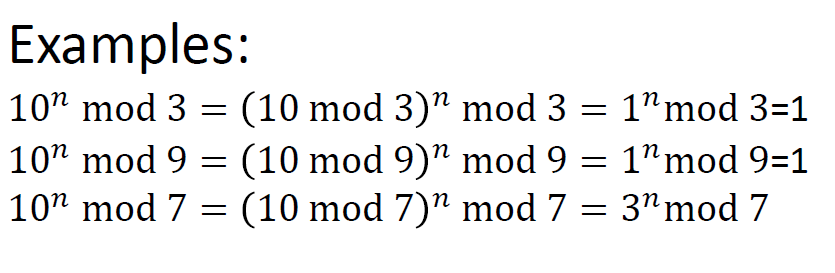
Inverse 逆元
Additive Inverse 加法逆元

Multiplicative Inverse 乘法逆元
注意



求法


e.g1

Different Sets


Multiplicative order 乘法阶



Fast Modular Exponentiation



Fermat's little theorem 费马小定理
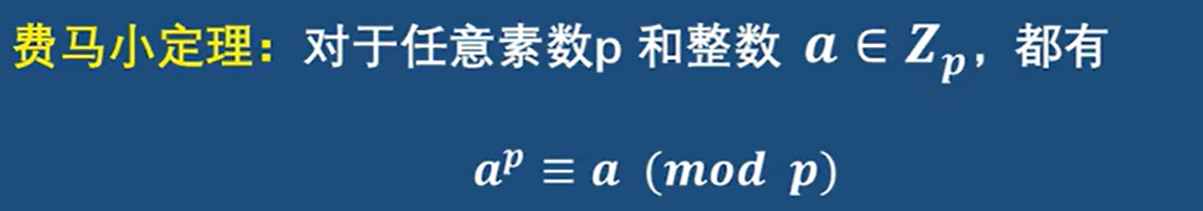





Euler’s Theorem
欧拉函数
它的定义是,对于一个正整数 n,φ(n) 是小于等于 n 的正整数中与 n 互质的数的个数。我们一般只关心个数而不关心到底都是谁

运算性质
 第三条:因为p是素数,所以任何小于p的正整数都与p互素,而小于p的正整数有1,2,3....P-1
第三条:因为p是素数,所以任何小于p的正整数都与p互素,而小于p的正整数有1,2,3....P-1
e.g

欧拉定理


L14 RSA
Leetcode372. Super Pow
感觉这节ppt讲的我云里雾里的
Public-key cryptosystems

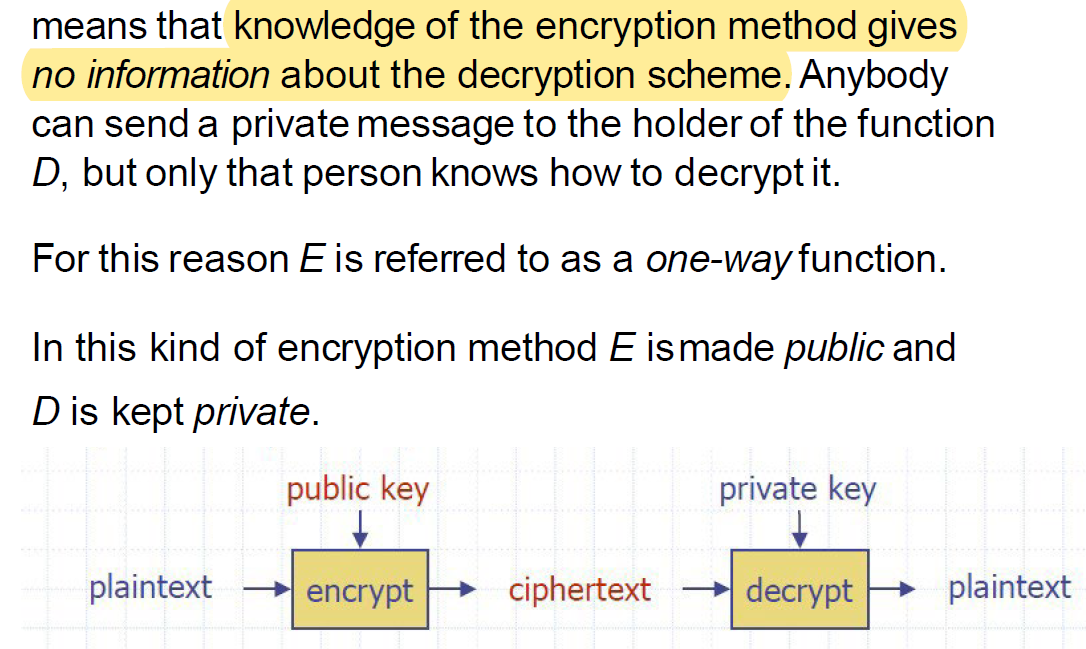
Turing's Code

Desiderata of RSA
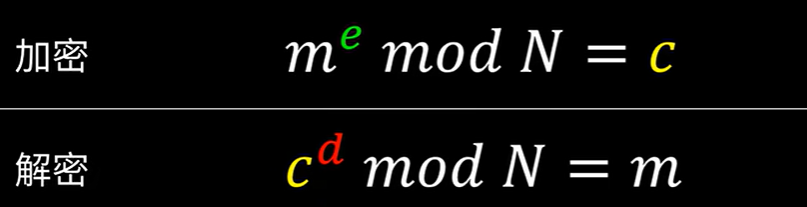

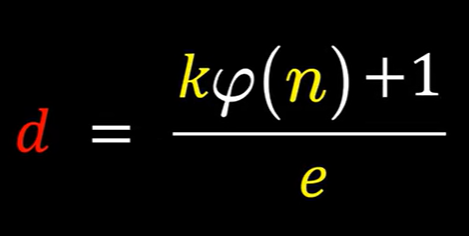
在大数上,Φ(n)的求解是不可行的

Euler's Theorem

Deriving RSA


RSA encryption

RSA Cryptosystem


Digital signature

Breaking RSA


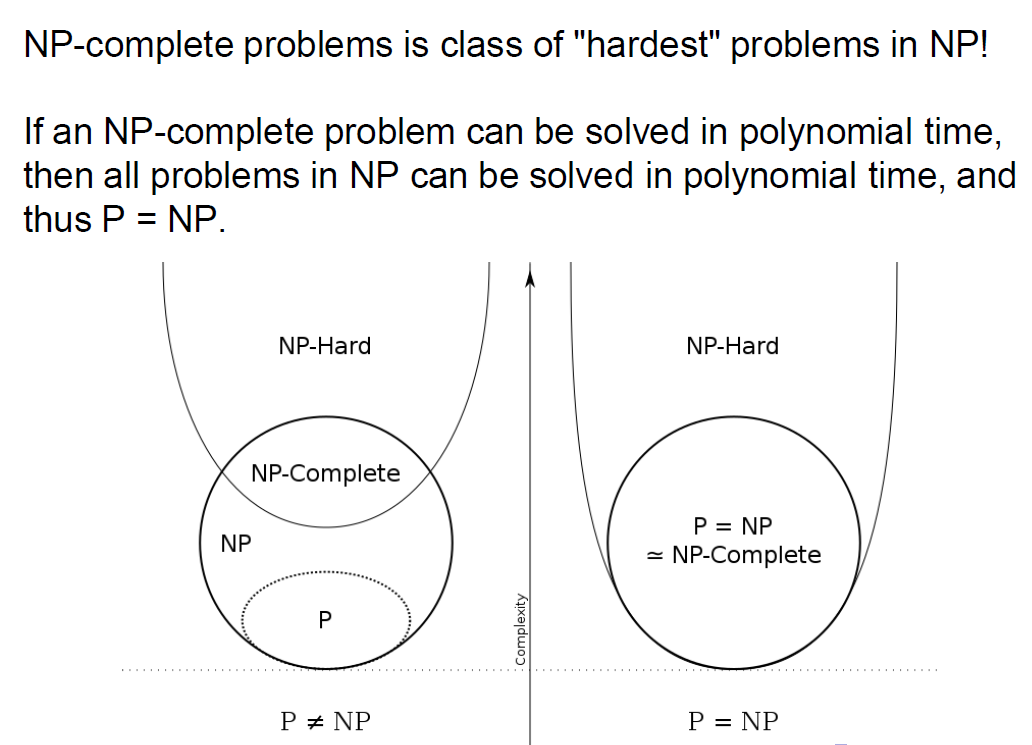
L15 P vs NP
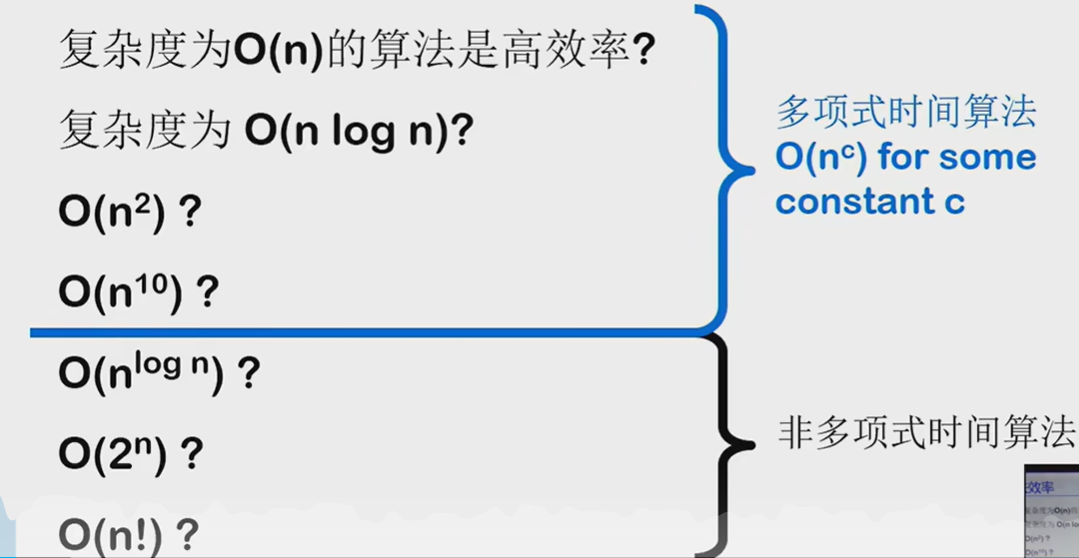
P: P类问题是指可以在多项式时间内(即时间复杂度为多项式函数的时间内)解决的问题。
NP:NP类问题是指能够在多项式时间内验证其解的问题。即使找到一个解可能很难,但一旦有了一个解,验证其正确性可以在多项式时间内完成。因为P类问题能在多项式时间内验证,所以P问题是NP问题,但是NP问题不一定是P问题
最优化问题(Optimization)转化成判定性问题
NP-complete: NP中最难的问题,所有NP都可以规约(reducibility,实例对应,输出一致,传递)到NPC问题,是NP-hard的子集
NP-hard: 多项式时间内不一定能验证
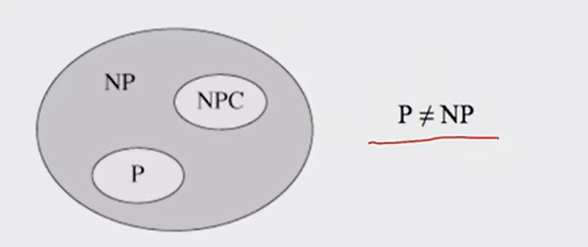

![]()
Decision/Optimization problems
(0,1)背包问题
Decision 决策问题: 给定一输入,判断是否
Optimization 优化问题: 得到最大化/最小化某值
优化问题可以转化为决策问题:给定一输入k,判断是否有解大于/小于k
如果能高效地回答决策问题,则我们能高效地解决优化问题
e.g
最优化问题:设G是一个边权为整数的连通图。求最小生成树inG的权值。
决策问题:设G是一个边权为整数的连通图,设k为整数。G有一个权重最大为k的生成树吗?
Complexity Class P

Efficient certification
对于决策问题X,一个有效的证明是一个算法B,它接受两个输入字符串s和t。字符串s是决策问题的输入。

Complexity Class N P

Deterministic
确定性算法:给定一个输入,只有一种最终结果,如计算数组总和
非确定性算法:给定一个输入,过程中会有多种分支,如求解数独
Non-deterministic Algorithm
(0,1)Knapsack

Polynomial-timereducibility
NP-hardness

NP-complete

SAT Boolean Satisfiability Problem 布尔可满足性问题
布尔可满足性问题(SAT): 给定一个由布尔变量组成的逻辑表达式,判断是否存在一种变量的赋值方式,使得该逻辑表达式的值为真(即“满足”该表达式)。
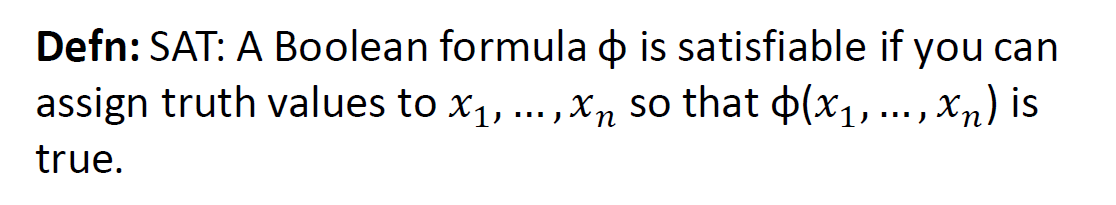
左侧有若干输入,中间若干逻辑门,右侧一个输出

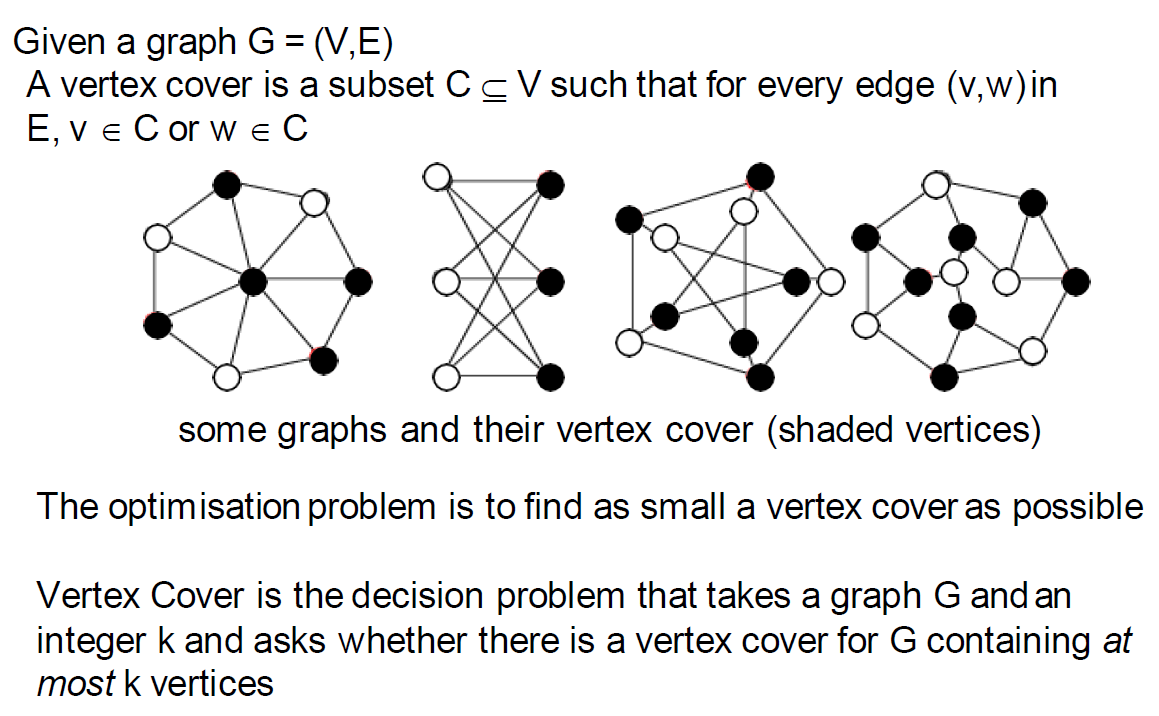
Vertex Cover(VC)



Turing Machine
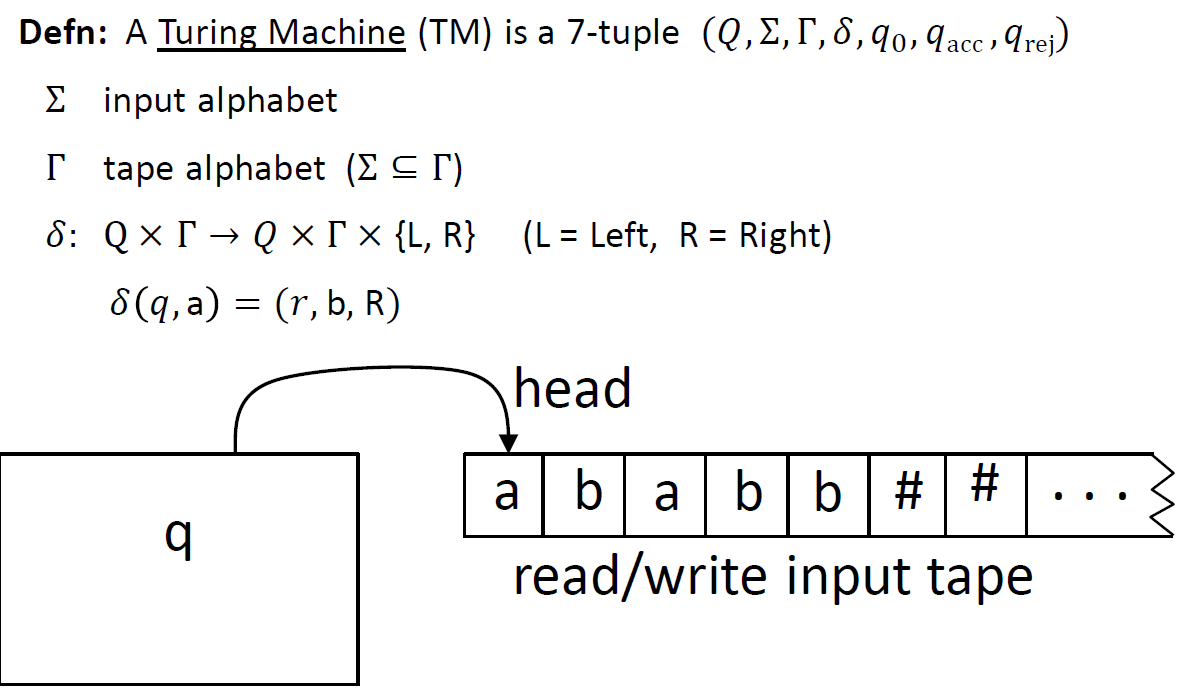
Simulate Turing Machine

Nondeterministic Turing Machine
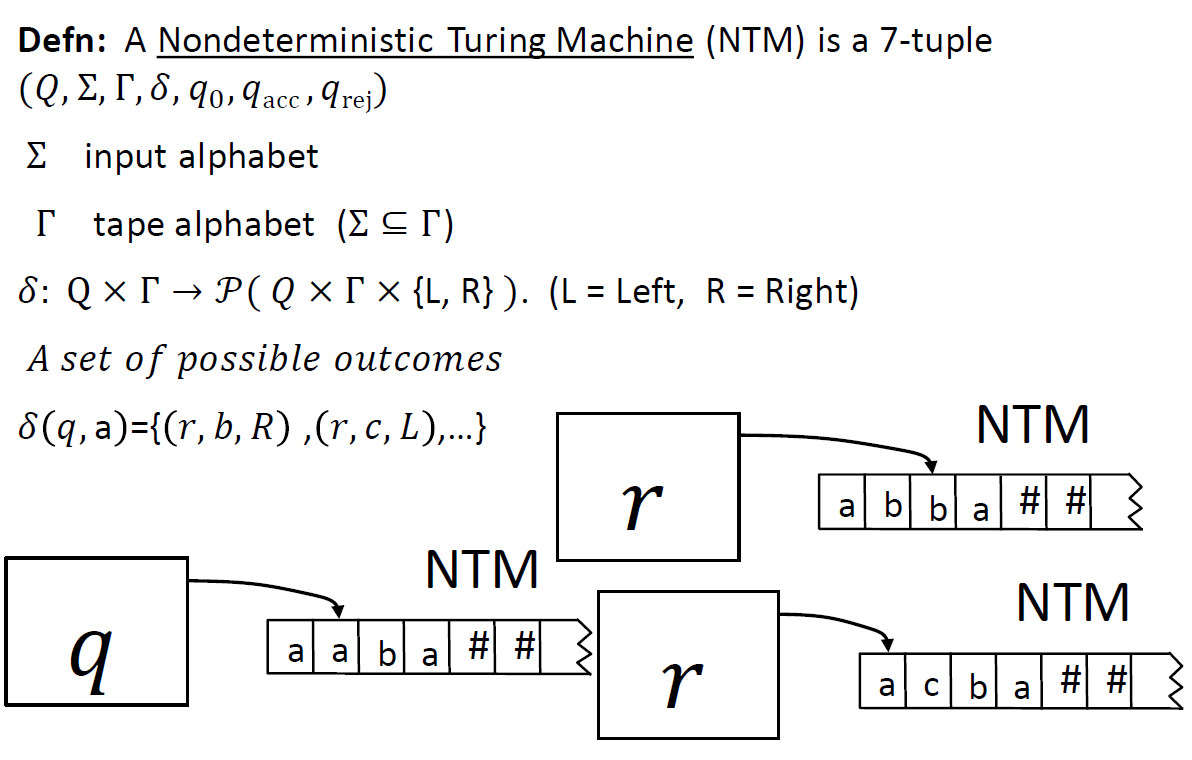
Cook-Levin
用来证明SAT问题是NP-complete的,证明任何算法都可以用Boolean Formula进行编码

CNF-SAT

3-SAT

具体来说,3-SAT 问题是指判断一个由布尔变量组成的逻辑公式是否存在一种变量赋值,使得整个公式为真。3-SAT 问题的公式由多个子句(clauses)组成,每个子句包含三个字面量(literals),字面量是布尔变量或它们的否定形式。

3-SAT 问题的NP-完全性: 3-SAT 问题是第一个被证明为NP-完全的问题,这意味着它具有以下特点:
- 它在NP类中:给定一个布尔变量的赋值,可以在多项式时间内验证公式是否为真。
- 它是NP-完全的:任何NP问题都可以在多项式时间内归约为3-SAT问题。因此,解决3-SAT问题的一个多项式时间算法可以解决所有NP问题。
因为3-SAT 是NP-完全的,这也意味着我们目前还不知道是否存在一种在多项式时间内解决所有3-SAT问题的算法。































 7501
7501

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








