LeetCode 354. 俄罗斯套娃信封问题

最新推荐文章于 2024-12-27 21:36:47 发布

Sasakihaise_

最新推荐文章于 2024-12-27 21:36:47 发布

阅读量146

点赞数

分类专栏： LeetCode LIS 文章标签： DP 二分贪心排序 LIS

本文链接：https://blog.youkuaiyun.com/Sasakihaise_/article/details/129750240

版权

LeetCode 同时被 2 个专栏收录

440 篇文章

订阅专栏

LIS

8 篇文章

订阅专栏

文章介绍了如何使用动态规划结合二分查找解决俄罗斯套娃信封问题。首先对信封按第一维度升序、第二维度降序排序，然后应用LIS问题的优化二分方法进行DP计算。在处理过程中，当新信封的高度大于当前DP数组的最大值时，更新DP数组。否则，通过二分查找找到合适位置插入新值，以保持数组递增。最终返回DP数组长度加1作为最大递增子序列的长度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

354. 俄罗斯套娃信封问题

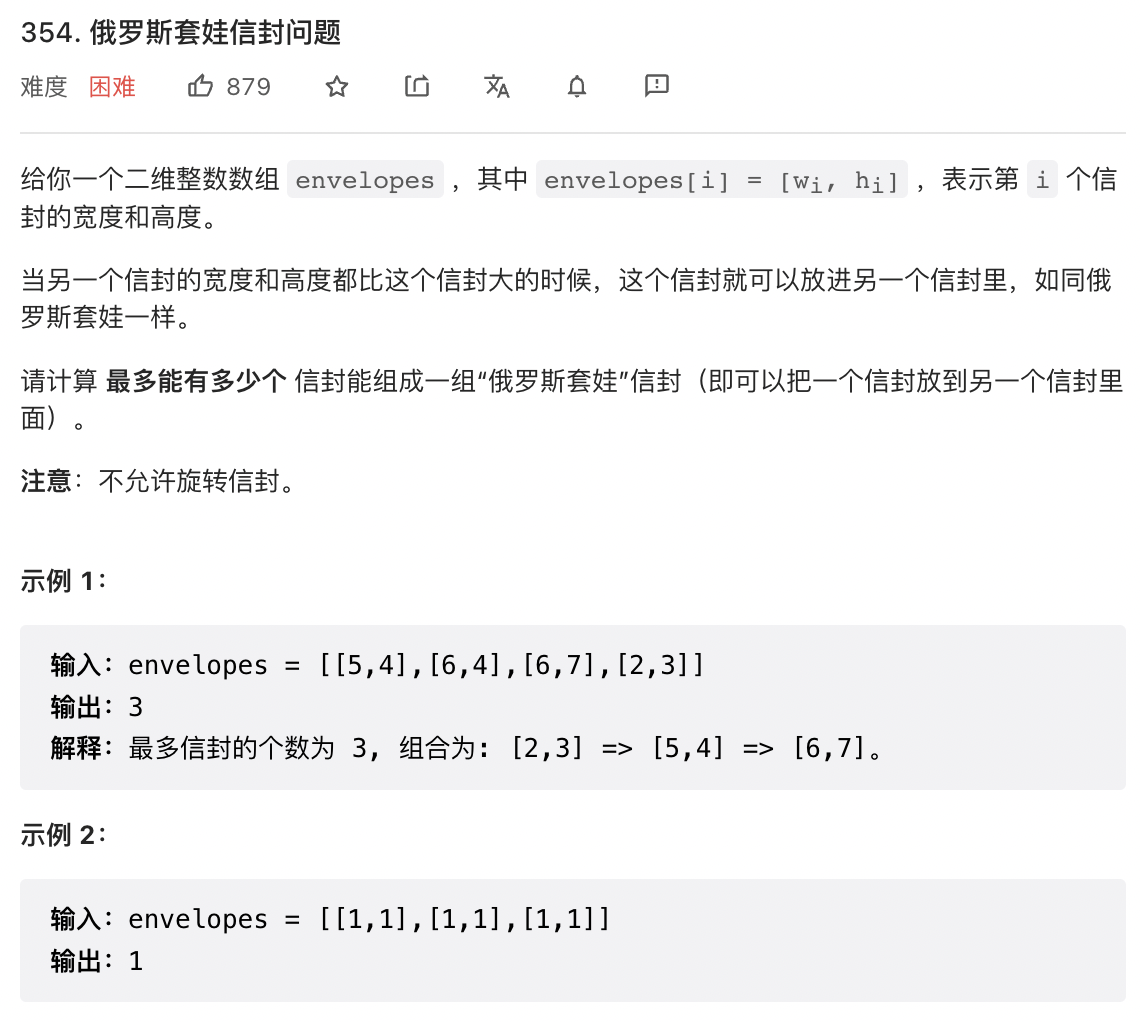
【DP + 二分】这是300. 最长递增子序列的扩展，把原来的一维扩展为二维了。首先我们先按照第一个维度从小到大排序，确保一个拓扑序的稳定，接下来第二个维度按照从大大小的顺序排序。为什么从大到小等下再解释。然后按照LIS问题的二分优化方法进行dp，由于第一个维度已经有序，所以这里dp的时候只需要看第二个维度。当env[i][1] > dp[l - 1]的时候把他放进去，这是可能就会有个问题是第一个维度相等。所以之前第二个维度是按照从大到小进行排序的，假如存在[2, 4] [2, 3]这种的，那么后面[2, 3]会触发二分插入的操作来把之前的[2, 4]更新掉。

class Solution {
    public int maxEnvelopes(int[][] env) {
        Arrays.sort(env, (a, b) -> a[0] != b[0]? a[0] - b[0]: b[1] - a[1]);
        int n = env.length, ans = 0;
        int[] dp = new int[n];
        dp[0] = env[0][1];
        for (int i = 1; i < n; i++) {
            if (env[i][1] > dp[ans]) dp[++ans] = env[i][1];
            else {
                int l = 0, r = ans;
                while (l <= r) {
                    int m = (l + r) >> 1;
                    if (dp[m] < env[i][1]) {
                        l = m + 1;
                    } else {
                        r = m - 1;
                    }
                }
                dp[l] = env[i][1];
            }
        }
        return ans + 1;
    }
}