floyd最短路径解法

         之前在解题过程中讲过的最短路算法Dijkstra和SPFA,但是,它们都是用来求单源最短路径的,比如说有一道题,先建一个图,然后要进行k次询问,问两个点的最短距离,那怎么办?用dijkstra或spfa跑k遍?显然不合理,如果k是10000,就已经受不了了,所以,就得用一种新的算法来解决。

好，下面有请我们今天的主角，floyd上场！

floyd的缺点是时间复杂度，跑一遍就是O(N^3)，特别难受，在数据范围小的时候可以用，但稍微大一点，比如N=1e5，就直接爆掉了。但它的优点是只跑一遍就能求导全源最短路径，任意两个点之间都有了。但是你会发现，求全源最短路径，就是用dijkstra跑N遍，也就是O(NlogN)的时间复杂度跑n遍。就是O(N^2logN),哎,还是比floyd快。

呃，虽然floyd很垃圾，但是我还是要讲，因为它思路简单，代码实现也简单

floyd的大体思想是先找一个中间点，再找起点和终点，如果起点直接到终点的距离比经过中间点再到终点的距离大，就进行更新

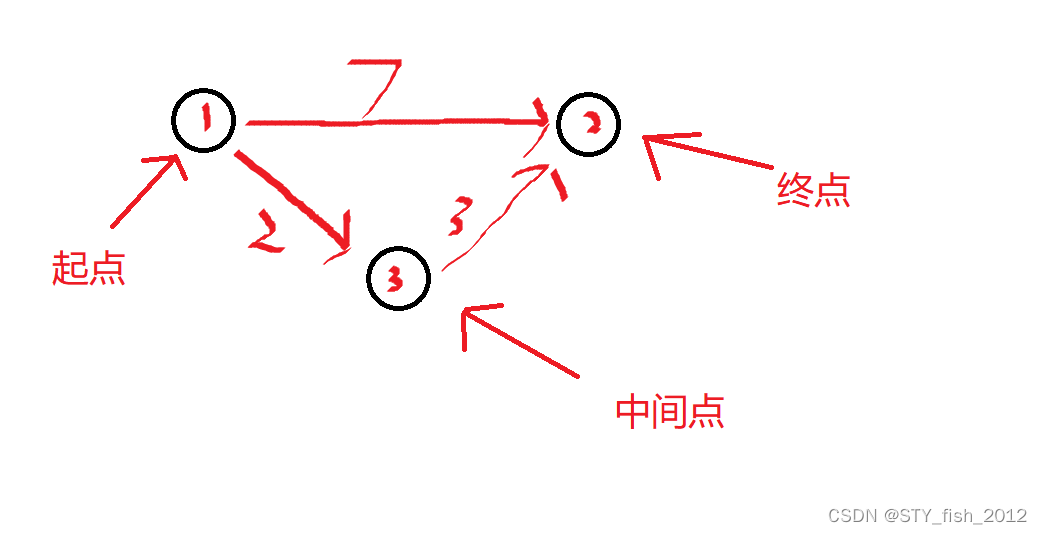
拿上图举例，1->2的距离是7，1到3再到2明显要小,明显更优,肯定是先经过中间点更短,这时我们就更新。 

讲完了大体思路,就先提一下初始化,首先肯定是先把所有的点都初始化为正无穷大,这里就设0x3f3f3f3f了,因为是求最小值,然后就是把a[i][i]都设为1,因为自己到自己不需要走。

所有的都弄完了，就是问什么答什么了，如果a[x][y]的值大于1e9,就走不过去，注意,不是等于0x3f3f3f3f,因为中间可能会在找的途中出现微小的差异,但不是很大

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e2 + 5;
int a[N][N];
int n, m;
signed main() {
	scanf("%lld%lld", &n, &m);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
			if (i == j) a[i][j] = 0;
			else a[i][j] = 0x3f3f3f3f;
	int u, v, w;
	for (int i = 1; i <= m; i++) {
		scanf("%lld%lld%lld", &u, &v, &w);
		a[u][v] = w;
	}
	for (int k = 1; k <= n; k++)
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= n; j++)
				a[i][j] = min(a[i][j], a[i][k] + a[k][j]);
	int k;
	scanf("%lld", &k);
	int x, y;
	while (k--) {
		scanf("%lld%lld", &x, &y);
		if (a[x][y] >1e9)printf("impossible\n");//走不过去
		else printf("%lld\n", a[x][y]);
	}
}