最短网络kruskal算法

题目描述

农民约翰被选为他们镇的镇长！他其中一个竞选承诺就是在镇上建立起互联网，并连接到所有的农场。当然，他需要你的帮助。约翰已经给他的农场安排了一条高速的网络线路，他想把这条线路共享给其他农场。为了用最小的消费，他想铺设最短的光纤去连接所有的农场。你将得到一份各农场之间连接费用的列表，你必须找出能连接所有农场并所用光纤最短的方案。每两个农场间的距离不会超过 100000。

输入描述

第一行：农场的个数，N。
第二行…结尾:后来的行包含了一个 N×N 的矩阵,表示每个农场之间的距离。理论上，他们是 N 行，每行由 N 个用空格分隔的数组成，实际上，他们限制在 80 个字符，因此，某些行会紧接着另一些行。当然，对角线将会是 0，因为不会有线路从第 i 个农场到它本身。

输出描述

只有一个输出，其中包含连接到每个农场的光纤的最小长度。

样例输入

4
0  4  9  21
4  0  8  17
9  8  0  16
21 17 16  0

样例输出

28

这差不多就是一道最小生成树的模版题

解决这道题先得了解最小生成树

最小生成树,顾名思义,它是一棵树

树与图最大的区别是什么?树是分层次的,并且,一棵树不能有环。

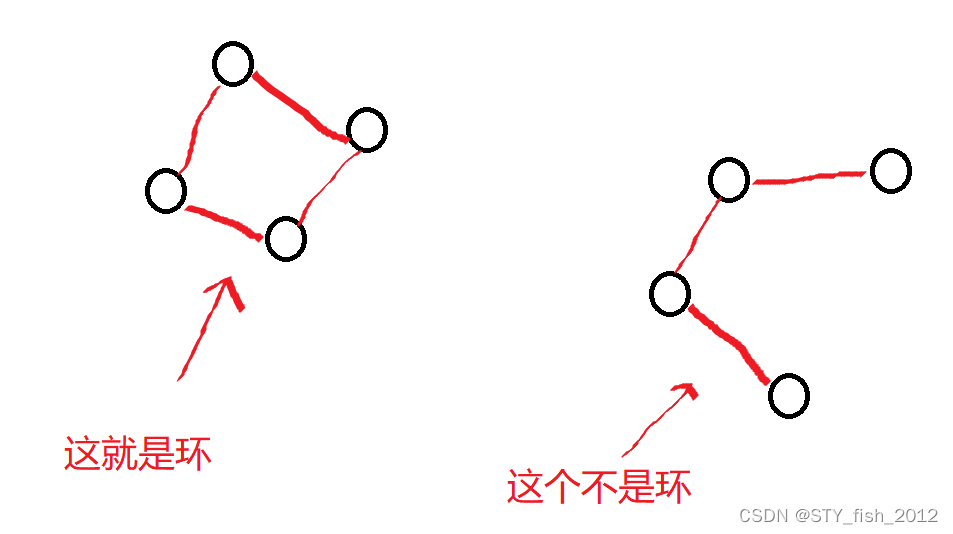
没有环有什么好处？这样可以保证所有的点联通，并且不会有多余的没用的边

把一个图变成一棵树，就需要去掉一些多余的边，使之没有环。然后，用剩下的边的边权相加，求出权值之和，删掉边之后形成树，权值之和最小的一棵，就是最小生成树

这道题求解的就是最小生成树

然后在这里，我们用kruskal来解决

kruskal算法的思路很简单，先建边，把边存进有3个值的结构体里面，三个元素u,v,w分别代表起点,终点,路径长度

然后我们按路径长度排个序,小的在前,大的在后,依次反填回图中,如果边x填进去时出现了环,就直接不要这条边了。把所有点都找一遍之后,就返回最终记录的权值和,得到答案

接着我们讲一下,怎么判断有没有环

这里我们需要一个数组f,f[i]的值就代表i的"老祖",老祖的概念就是与它连接的最深的点,如果两个点的老祖相同,那这两个点肯定就有环了

找老祖函数

int find(int x){
	if(f[x]!=x)f[x]=find(f[x]);
	return f[x];
}

没有环就直接加

#include<bits/stdc++.h>
using namespace std;
const int N=2e5;
int cnt;
struct node{
	int u,v,w;
}a[N];
int f[N];
int n;
int find(int x){
	if(f[x]!=x)f[x]=find(f[x]);
	return f[x];
}
bool cmp(node a,node b){
	return a.w<b.w;
}
int kru(){
	sort(a+1,a+1+cnt,cmp);
	for(int i=1;i<=cnt;i++)f[i]=i;
	int sum=0;
	for(int i=1;i<=cnt;i++){
		int u=a[i].u;
		int v=a[i].v;
		int w=a[i].w;
		if(find(u)==find(v))continue;
		else{
			f[find(u)]=find(v);
			sum+=w;
		}
	}
	return sum;
}
signed main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			int x;
			scanf("%d",&x);
			a[++cnt]=node{i,j,x};
		}
	}
	printf("%d",kru());
}