A Simple Problem with Integers 线段树（POJ 3468 区间查询 区间值更改 ）

A Simple Problem with Integers（点击转到）

Time Limit: 5000MS		Memory Limit: 131072K
Total Submissions: 140821		Accepted: 43675
Case Time Limit: 2000MS

Description

You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.

Input

The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of Aa, Aa+1, ... , Ab.

Output

You need to answer all Q commands in order. One answer in a line.

Sample Input

10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

Sample Output

4
55
9
15

Hint

The sums may exceed the range of 32-bit integers.

Source

POJ Monthly--2007.11.25, Yang Yi

1.题目含义：

    给定Q (1 ≤ Q ≤ 100,000)个数A1,A2 … AQ,， 以及可能多次进行的两个操作:
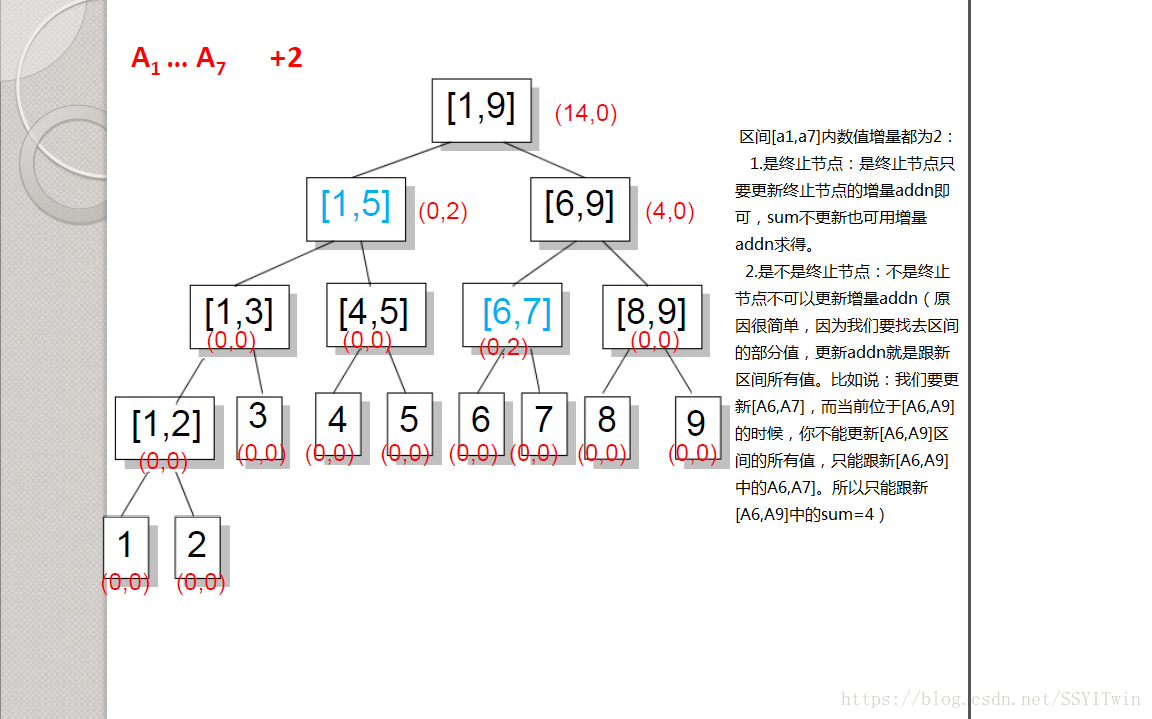
       1.1 对某个区间Ai … Aj的每个数都加n(n可变）

       1.2求某个区间Ai … Aj的数的和。

2.思路：

   2.1在增加时（Add()函数），如果要加的区间正好覆盖一个节点，则增加其节点的addn值，不再往下走，否则要更新sum(加上本次增量),再将增量往下传。这样更新的复杂度就是O(log(n))

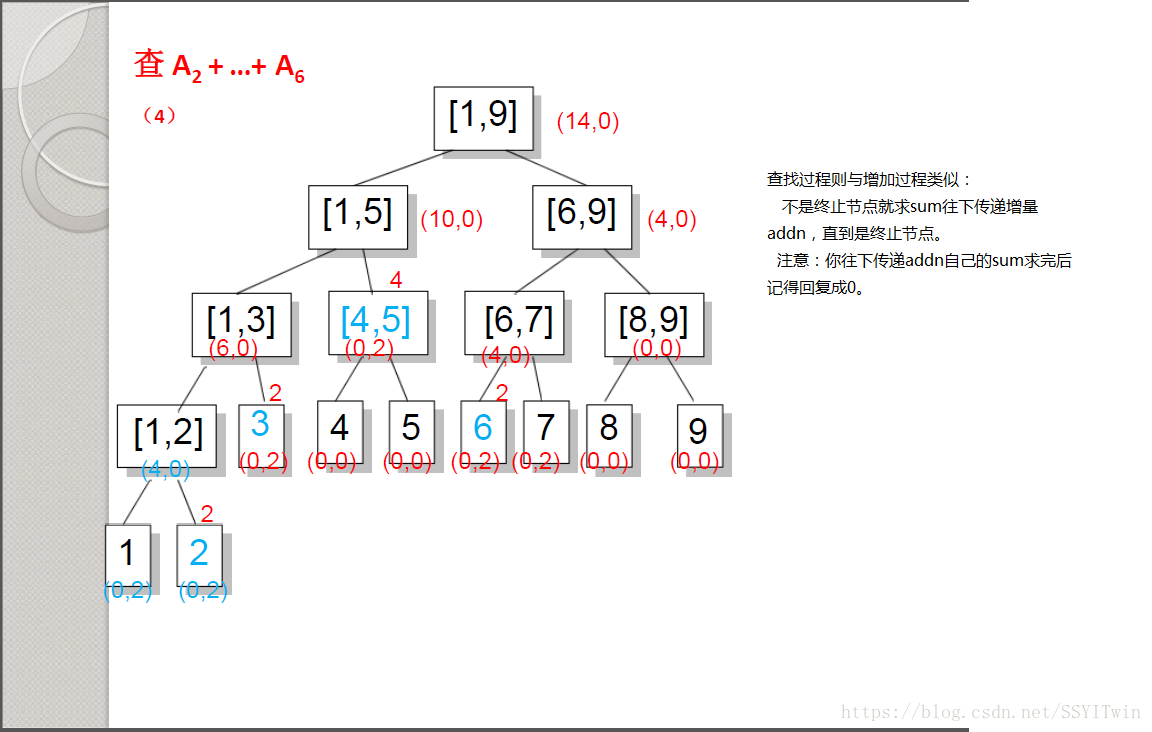
   2.2在查询时(Query()函数)，如果待查区间不是正好覆盖一个节点，就将节点的addn往下带，然后将addn代表的所有增量累加到sum上后将addn清0，接下来再往下查询。 一边查询，一边Inc往下带的过程也是区间分解的过程，复杂度也是O(log(n))

 

3.线段树：

   3.1线段树适用于和区间统计有关的问题，当题目中有 “区间”，‘’任意“，多次”等词汇的时候，便要考虑用线段树分区间进行求解。

   3.2线段树的过程就分为：建线段树——插入数据——查询更新（题目要求）的一个过程。

4.注意读入整数后，将后面的回车符用getchar()读走后，再读字符。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,q;
struct node
{
	int l;
	int r;
	long long  sum;
	long long  addn;
}tree[400010];
void BuildTree(int root,int l,int r)
{
	tree[root].l=l;
	tree[root].r=r;
	tree[root].sum=0;
	tree[root].addn=0;
	int mid=(l+r)/2;
	if(l!=r)
	{
		BuildTree(root*2+1,l,mid);
	    BuildTree(root*2+2,mid+1,r);
	}
} 
void Insert(int root,int i,int v)
{
	if(tree[root].l==i&&tree[root].r==i)
	{
		tree[root].sum=v;
		return ;
	}
	tree[root].sum=tree[root].sum+v;//边插入边保存sum的值 
	int mid=(tree[root].l+tree[root].r)/2;
	if(i<=mid)
	   Insert(2*root+1,i,v);
	else
	  Insert(2*root+2,i,v); 
}
void Add(int root,int s,int e,long long addn)
{
	if(tree[root].l==s&&tree[root].r==e)
	{
		tree[root].addn=tree[root].addn+addn;
		return ;
	}
	tree[root].sum=tree[root].sum+(e-s+1)*addn;
	int mid=(tree[root].l+tree[root].r)/2;
	if(e<=mid)
	{
		Add(2*root+1,s,e,addn);
	}
	else if(s>=mid+1)
	{
		Add(2*root+2,s,e,addn);
	}
	else
	{
		Add(2*root+1,s,mid,addn);
		Add(2*root+2,mid+1,e,addn);
	}
}
long long Query(int root,int l,int r)
{
	if(tree[root].l==l&&tree[root].r==r)
	{
		return tree[root].sum+(tree[root].r-tree[root].l+1)*tree[root].addn;
	}
	tree[root].sum=tree[root].sum+(tree[root].r-tree[root].l+1)*tree[root].addn;
	int mid=(tree[root].l+tree[root].r)/2;
	Add(2*root+1,tree[root].l,mid,tree[root].addn);
	Add(2*root+2,mid+1,tree[root].r,tree[root].addn);
	tree[root].addn=0;//增量往下传递，自身的改为0 
	if(r<=mid)
	{
		return Query(2*root+1,l,r);
	}
	else if(l>=mid+1)
	{
		return Query(2*root+2,l,r);
	}
	else
	{
		return Query(2*root+1,l,mid)+Query(2*root+2,mid+1,r);
	}
} 
int main()
{
	scanf("%d%d",&n,&q);
	BuildTree(0,1,n);
	for(int i=1;i<=n;i++)
	{
		int num;
		scanf("%d",&num);
		Insert(0,i,num);
	}	
	char ss;
	int a,b,c;
	for(int i=0;i<q;i++)
	{
		getchar();
		scanf("%c",&ss);
		if(ss=='Q')
		{
			scanf("%d%d",&a,&b);
			printf("%lld\n",Query(0,a,b));
		}
		else
		{
			scanf("%d%d%d",&a,&b,&c);
			Add(0,a,b,c);
		}
	}
	return 0;
}