微积分引子

微积分

---

只是想写一写加深印象而已，作者是个蒟蒻。（借鉴了很多其他题解的解释）

看了一些大佬们关于微积分的讲解，逐步摸清了微积分的轮廓。
对于微积分最关键也是源头来源于不规则几何形状的求解。

譬如举个例子：

这个一次函数和二次函数之间围成的矩形怎么求解？（思考一下）

在这里我们就需要用到极限思想去想方设法去用规则的图形逼近这个不规则的曲面的面积，我们可以用三角形。

请注意并不是可以将三角形随便乱摆，我们要尽可能要用三角形覆盖掉尽可能多的面积，也就是初中所学的关于此类问题三角形的最大值，其实作者做的这个图不太完美，大家可以仔细观察可以得到，中间的三角形的面积等于左右两旁三角形面积和的4倍（误差是由精度造成的）。然后就像这样再以各两旁三角形为基础往各自两个曲面尽可能的放进一个三角形。

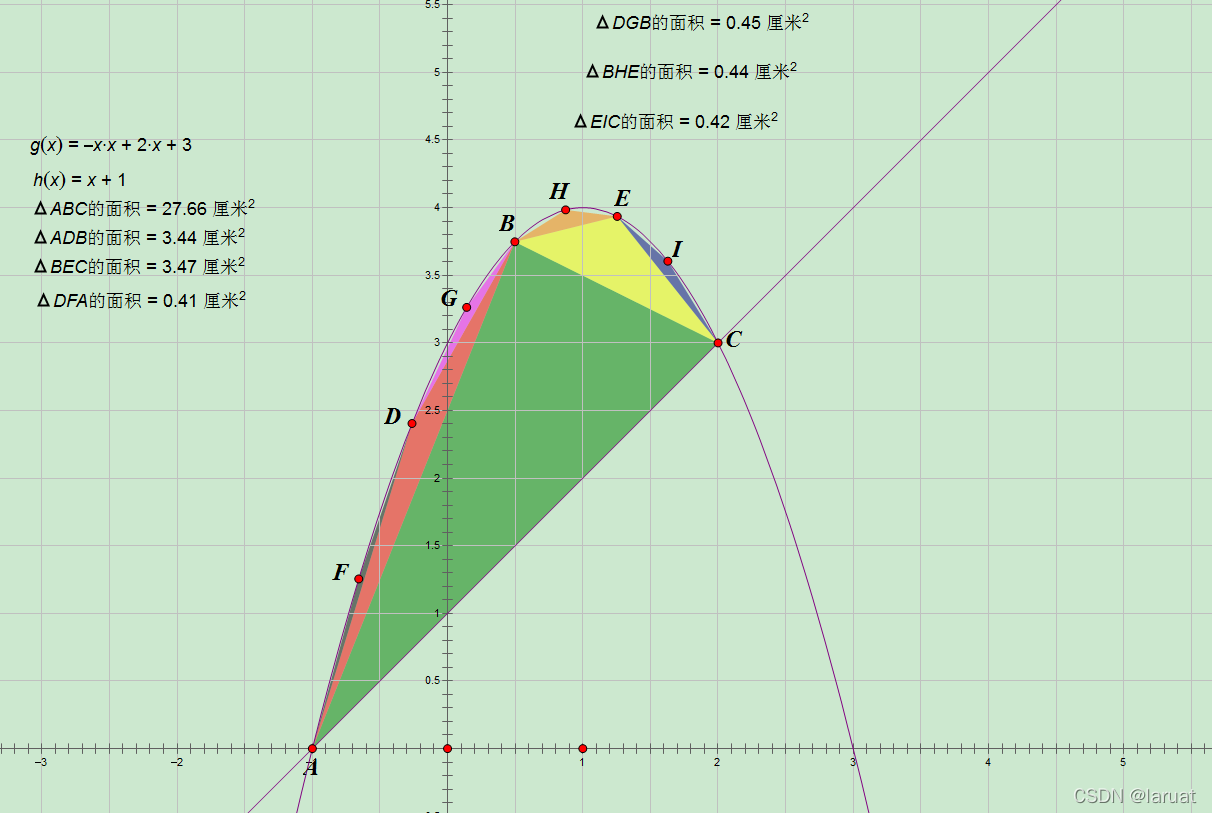
可以发现这新加入的四个三角形又是前两个三角形的面积和的1/4倍。

那么我们可以一直放三角形一直放到无限接近于此曲面的面积。假设我放了n轮三角形，（已经无限接近曲面面积）。三角形ABC面积为x。
则有

$Sn=x+\frac{1}{4}x+(\frac{1}{4}{)}^{2}x+...+(\frac{1}{4}{)}^n$

很明显这是一个等比数列求和，套进去。

等比数列：

$Su{m}_n=\frac{a1(1-q^n)}{1-q}x$

$Sn=\frac{4-<}{3}$