树B

Description

已知无向连通图G由N个点，N-1条边组成。每条边的边权给定。现要求通过删除一些边，将节点1与另M个指定节点分开，希望删除的边的权值和尽量小，求此最小代价。

Input
每个输入文件中仅包含一个测试数据。

第一行包含两个整数N,M。

第二行至第N行每行包含3个整数,A、B、C，表示节点A与节点B有一条边相连，边权为C。

第N+1行至第N+M行每行包含一个整数X，表示要求与节点1分开的节点。

Output

输出文件仅包含一个整数，表示最小代价。

Sample Input
3 2
1 2 3
1 3 5
2
3

Sample Output
8

Data Constraint

Hint

对于20%的数据，2<=N<=10
对于100%的数据，2<=N<=10^6

.
.
.
.
.
分析
树形DP

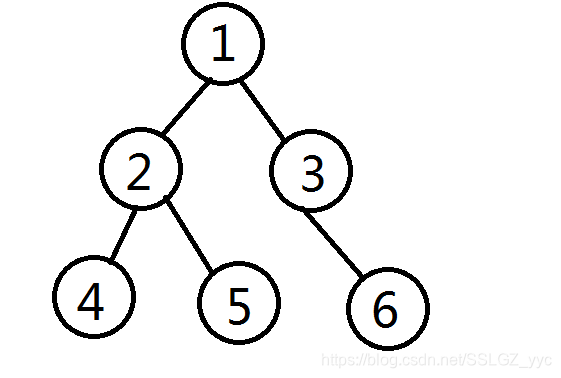
如上图，假设我们要把点3、4、5与点1分开，可以选择将它们单独分开，也可以通过删除它们的公共祖先（不一定是LCA）与它们的连边把它们分开。例如，如果要把点4、5与点1分开，那么我们可以删除边（2，4）和边（2，5），单独分开点4和点5，也可以删除边（1，2），把以点2为根的子树与点1分开。这样，设 表示以点i为根的子树删去的边的权值和的最小值，那么 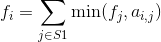，其中S1为 的孩子的集合， 表示点i到点j的边的权值。最终的答案就是 。注意，如果用DFS实现，那么到一个需要与点1分开的点（设为点k）时，将 设为1即可，不需要向下递归（毕竟这样没用）。

.
.
.
.
.
.
程序：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

bool bz[1000001];
int f[1000001],cnt=0,head[1000001];

struct edge
{
	int to,from,w;
}e[4000001];

void add(int x,int y,int z) 
{ 
	e[++cnt].to=y;e[cnt].from=head[x];head[x]=cnt;e[cnt].w=z;
	e[++cnt].to=x;e[cnt].from=head[y];head[y]=cnt;e[cnt].w=z;
}

void work(int x,int father)
{
	int sum=0,r;
	for (int i=head[x];i;i=e[i].from)
		if (e[i].to==father) r=e[i].w; else
		{
			work(e[i].to,x);
			sum+=f[e[i].to];
		}
	if (x==1) f[x]=sum; else
	if (bz[x]) f[x]=r; else f[x]=min(sum,r);
}

int main()
{
	int n,m;
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n-1;i++)
	{
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
	}
	memset(bz,false,sizeof(bz));
	for (int i=1;i<=m;i++)
	{
		int x;
		scanf("%d",&x);
		bz[x]=true;
	}
	work(1,0);
	printf("%d",f[1]);
	return 0;
}