异或

SarvaTathagata是个神仙，一天他在研究数论时，书上有这么一个问题：求不超过n两两的数的gcd。
SarvaTathagata这么神仙的人当然觉得这个是sb题啦。学习之余，他还发现gcd的某一个特别好的性质：如果有两个数i,j满足gcd(i,j)=i^j(这里的为c++中的异或)的话，那么这两个数组成的数对(i,j)就是一个nb的数对(这里认为(i,j)和(j,i)为相同的，并不需要计算2次)。
当然，SarvaTathagata并不会只满足于判断一个数对是否nb，他还想知道满足两个数都是不超过n并且nb的数对有多少个。
由于SarvaTathagata实在是太神仙了，他认为这种题实在是太简单了。于是他找到了你，看看你是否能解决这个问题。

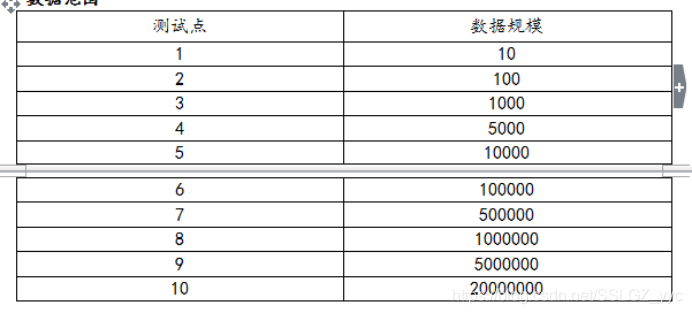
输入

共一行一个整数n，含义如题所述。
输出

一行一个整数，表示nb的数对的个数。
输入样例

样例输入1
12
样例输入2
123456
输出样例

样例输出1
8
样例输出2
214394
说明

提示
样例1中共有八对，分别是： {2,3},{4,5},{4,6},{6,7},{8,9},{8,10},{8,12},{10,11}

.
.
.
.
.
分析
通过暴力找规律得
gcd(a,b)=a-b=a^b
则求有几个a,b满足a-b=a^b即可
.
.
.
.
.
.
暴力：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int n,tj=0;

int gcd(int a,int b)
{
	if (b==0) return a; else return gcd(b,a%b);
}

int main()
{
	scanf("%d",&n);
	for (int i=2;i<=n-1;i++)
		for (int j=i+1;j<=n;j++)
		{
			int bz=i^j;
			if (bz==gcd(i,j))
			{
				tj++;
			}
		}
	cout<<tj;
	return 0;
}

.
.
.
.
.
.
正解：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int n,x,b,r,tj;

int main()
{
    scanf("%d",&n);
    for (int i=1;i<=n/2;i++)
    {
    	int j=2;
        while (i*j<=n)
        {
        	x=i^(j*i);
            b=i*j-i;
            if (x==b) tj++;
            j++;
        }
    }
    printf("%d",tj);
    return 0;
}