非线性回归与曲线回归的区别

在SPSSAU(在线SPSS)数据分析平台中，非线性回归和曲线回归是两种处理非线性关系的分析方法，但它们存在本质区别。以下是两者的详细对比：

1. 基本概念差异

曲线回归

• 本质：属于"本质线性模型"
• 原理：通过数学转换将非线性关系转换为线性关系进行分析
• SPSSAU实现路径：【进阶方法】→【曲线回归】

非线性回归

• 本质：属于"本质非线性模型"
• 原理：采用数值迭代方法直接拟合非线性关系
• SPSSAU实现路径：【进阶方法】→【非线性回归】

2. 核心区别对比表

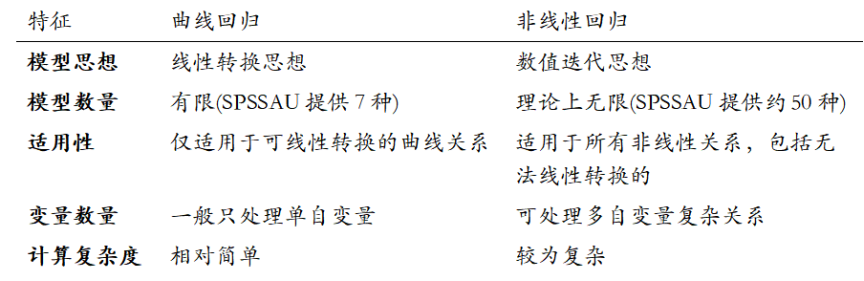
3. 具体差异详解

(1) 模型拟合方法不同

• 曲线回归：先将变量进行数据转换(如对数转换、平方转换等)，然后使用线性回归方法分析转换后的数据
• 非线性回归：直接使用迭代算法(如Levenberg-Marquardt算法)寻找最优参数，无需数据转换

(2) 适用场景不同

• 曲线回归适用于：
  • 常见简单曲线关系(如二次曲线、指数曲线等)
  • 可通过简单转换变为线性关系的情况
  • 单自变量分析
• 非线性回归适用于：
  • 复杂曲线关系(如S型曲线、生长曲线等)
  • 无法通过简单转换变为线性关系的情况
  • 多自变量复杂关系分析

(3) SPSSAU平台提供的模型

• 曲线回归模型：7种常见模型
  • 二次曲线(Quadratic)
  • 三次曲线(Cubic)
  • 对数曲线(Logarithmic)
  • 指数曲线(Exponential)
  • 复合曲线(Compound)
  • 增长曲线(Growth)
  • S曲线(S)
• 非线性回归模型：约50种模型，涵盖各类复杂非线性关系

4. 实际应用建议

1. 先做散点图：观察变量间关系形态，判断是否为非线性关系
2. 简单关系优先尝试曲线回归：对于常见简单曲线关系，曲线回归更简便
3. 复杂关系使用非线性回归：当曲线回归无法满足或拟合效果不佳时，转向非线性回归
4. 模型评估：无论使用哪种方法，都需要评估模型拟合优度(R²等指标)和残差分析

在SPSSAU(网页SPSS)平台中，两种方法都有清晰的模块划分和操作指引，用户可根据实际数据特征选择最适合的分析方法。