模糊层次分析法原理与案例软件操作分析

模糊层次分析法是在传统层次分析法（AHP）的基础上，结合模糊理论发展而来的一种决策方法。它能够有效处理决策问题中的不确定性和模糊性，广泛应用于学术研究和实际决策中。本文将详细介绍FAHP的原理，并通过SPSSAU(在线SPSS)平台演示其操作步骤。

一、模糊层次分析法原理

1.1 模糊互补矩阵的建立

在传统AHP中，我们使用判断矩阵来比较各指标的相对重要性。而在FAHP中，我们使用模糊互补矩阵。模糊互补矩阵的特点如下： 

- 对角线上的元素均为0.5，表示自己与自己是同等重要的。 

- 对称位置的两个元素相加等于1。

例如，若指标二对指标一的重要性为0.4，则指标一对指标二的重要性为0.6。

1.2 模糊权重的计算

模糊权重的计算公式如下：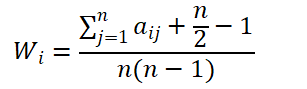

其中，aij是模糊互补矩阵中的元素，n是指标的数量。

1.3 模糊一致性检验