探索性因子分析完全解读：理论与SPSSAU实践指南-优快云博客

探索性因子分析作为多元统计分析的核心方法，在心理学、教育学、市场研究等领域有着广泛应用。它能够帮助研究者理解变量间的内在结构，将多个观测变量浓缩为少数几个潜在因子，从而简化数据结构和揭示变量间的潜在关系。本文将系统介绍探索性因子分析的理论框架、核心指标及其在SPSSAU平台上的实现过程。

一、探索性因子分析的基本原理

1、什么是探索性因子分析？

探索性因子分析是一种数据降维和结构探索的统计方法，其核心目的是从一组观测变量中提取出少数几个潜在因子，这些因子能够解释原始变量的大部分变异。

上图展示了探索性因子分析的三个主要目的，包括数据降维、结构探索和变量筛选，帮助研究者从大量变量中提取核心信息。

2、因子分析的理论基础

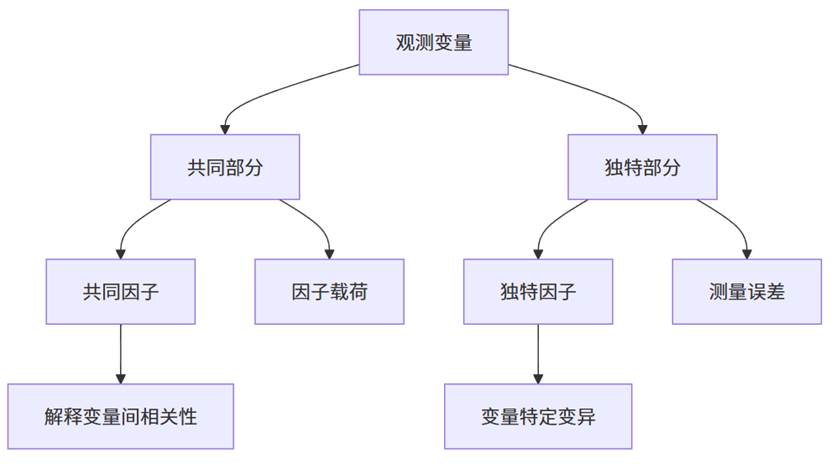
因子分析基于"共同因子模型"，认为每个观测变量都可以表示为共同因子和独特因子的线性组合。因子分析的理论模型示意图如下图，展示观测变量如何被分解为共同部分和独特部分，共同部分由潜在因子解释。

二、探索性因子分析完整流程

在SPSSAU中进行探索性因子分析遵循清晰的逻辑流程：

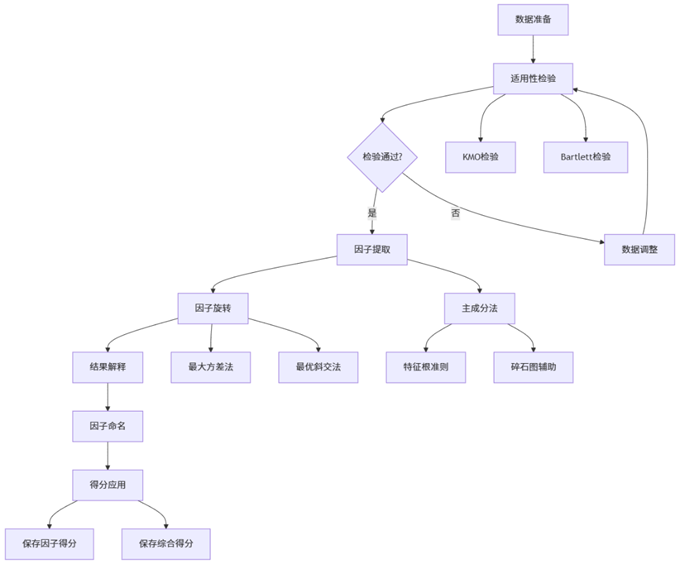
上图展示了SPSSAU中探索性因子分析的完整工作流程，从数据准备到结果应用的六个关键步骤，确保分析的系统和规范。

这一完整流程确保了因子分析的系统性和结果的可解释性。SPSSAU平台将这一复杂过程自动化，用户只需拖拽变量并设置相应参数即可获得专业级的因子分析结果。

三、探索性因子分析核心指标解析

探索性因子分析涉及多类统计指标，它们共同构成了完整的因子分析评估体系。

1) 适配性检验类（决定是否能做 EFA）

相关系数矩阵（Correlation matrix）
含义：展示变量之间的双变量线性相关程度。EFA 的前提是变量之间存在一定程度的相关性（既不能完全独立，也不能高度冗余）。
理论意义：若多数变量互相关很低，EFA 无法“浓缩信息”；若高度相关（接近 1），说明冗余，需要合并或删项。
KMO（Kaiser-Meyer-Olkin）测度
含义：衡量样本对于因子分析的适合度，从变量与变量之间相关的平方和与偏相关的平方和计算得来（总体或逐项均可）。
理论意义：KMO 越高，说明每个变量与其他变量的共同信息越多、偏相关越少，因子分析越可靠。常用阈值（理论指引）：>0.8 非常适合，0.7–0.8 比较适合，0.6–0.7 可勉强使用，<0.6 需谨慎。
Bartlett 球形度检验（Bartlett’s test）
含义：检验相关矩阵是否与单位矩阵显著不同（零假设：变量间不相关）。
理论意义：当 p 值显著（小于显著性水平）时，拒绝零假设，说明相关矩阵适合用于 EFA。
MSA（Measure of Sampling Adequacy）逐项指标
含义：KMO 的逐项版本，用于判断单个变量与其他变量的共性贡献。
理论意义：低 MSA 表明某个变量与其他变量信息共享较少，可能成为删除候选；过高则提示与其他变量重叠严重（亦需审视）。

2) 提取因子相关指标（信息量与选择依据）

特征根（Eigenvalues）与 Kaiser 准则
含义：每个主成分/因子解释的方差量，特征根 > 1 常被视为保留的一个简单准则（Kaiser 准则）。
理论意义：特征根反映该因子对原始变量总方差的贡献。单凭特征根可能过于机械，需结合碎石图与专业知识。
方差解释率（Variance Explained）与累积方差
含义：因子分别解释的方差占总方差的比例；累积方差表明若干因子合并后解释的总信息百分比。
理论意义：此指标用于衡量因子集合对原始信息的保留程度。不同领域对“充分解释”的阈值不同（心理测量可能要求较高，应用研究可适当放宽）。
碎石图（Scree Plot）
含义：按特征根大的顺序绘制，辅助判别“陡降点”后的拐点位置，拐点之前的因子通常被保留。
理论意义：直观工具，强调由陡降到平稳的转折处对应合理的因子数，但主观判断成分仍需领域知识配合。

3) 因子载荷与共同度（决定变量归属与解释）

因子载荷系数（Factor Loadings）
含义：变量在某因子上的线性相关系数（或相关度的表征），绝对值越大，说明该变量与该因子的关联越强。
理论意义：载荷用于判断变量归属某一因子（常用阈值绝对值 >0.4/0.5 做为归属参考），并为因子命名提供直接依据。
共同度（Communality）
含义：某个变量被提取因子解释的方差比例，数学上是该变量在提取模型下的方差保留量。
理论意义：共同度高说明变量的大部分方差被因子结构解释；共同度低（例如 <0.4）说明该变量可能不适合当前因子模型。
载荷图 / 载荷热力提示
含义：可视化每个变量在各因子上的载荷及显著性（软件常用颜色标注不同阈值）。
理论意义：帮助识别交叉载荷（一个变量在多个因子上载荷明显），提示需要用专业判断进行归属或删除。

4) 旋转与解释（提高可解释性）

正交旋转（Orthogonal rotation，例：Varimax 最大方差法）
含义：保持因子间正交（互不相关），通过变换使载荷矩阵更“稀疏”，即每个变量在少数因子上高载荷。
理论意义：便于解释与命名，适用于假设潜因子相互独立的情形。
斜交旋转（Oblique rotation，例：Promax/Oblimin 最优斜交法）
含义：允许因子之间相关，适合潜在因子之间具有现实相关性的场景（很多社会科学变量间并非互斥）。
理论意义：若理论上因子可能相关，斜交旋转能更真实地反映变量结构，但解释上需区分因子载荷与因子间的相关矩阵。

5) 得分与权重（从因子到复合指标）

成分/因子得分系数矩阵（Component Score Coefficients）
含义：把标准化后的原始变量线性组合为因子得分的系数矩阵。
理论意义：给出如何计算单个样本在每个因子上的得分（可用于个案排序、后续回归或聚类分析）。
线性组合系数、综合得分系数与权重计算
含义：将因子得分系数按因子方差贡献加权合成综合得分，并归一化以得到指标权重。
理论意义：提供一种以因子分析为基础的客观权重计算方法，便于将多指标汇总为单一评分，但要注意归一化步骤与解释局限（基于标准化数据、线性假设）。

四、SPSSAU各分析表格的作用与解读

1. KMO和Bartlett检验表

这个表格是因子分析的"入场券"，用于判断数据是否适合进行因子分析。如果KMO值过低或Bartlett检验不显著，说明数据不适合做因子分析，需要重新考虑变量选择或数据预处理。

2. 方差解释率表格

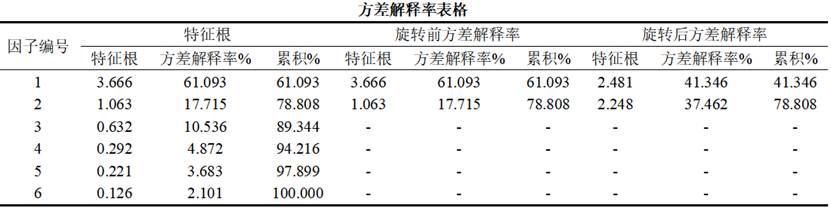
此表格展示了因子分析的信息浓缩效果，告诉我们提取的因子能够保留原始变量多少信息。累积方差解释率越高，说明因子对原始信息的保留越充分。

3. 旋转后因子载荷系数表格

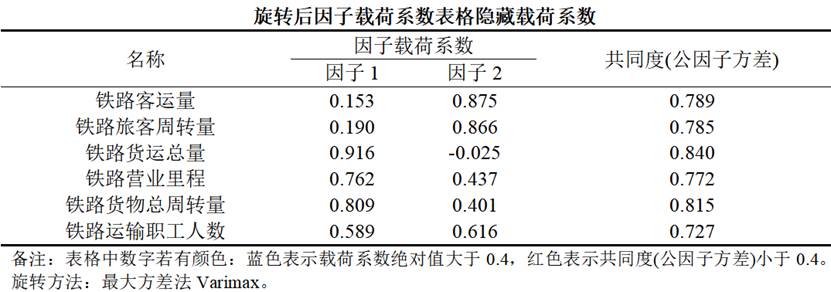
这是因子分析的核心结果表格，显示了每个变量在各个因子上的负荷情况。通过这个表格，我们可以了解变量的归类情况，为因子命名提供依据。

4. 成分得分系数矩阵

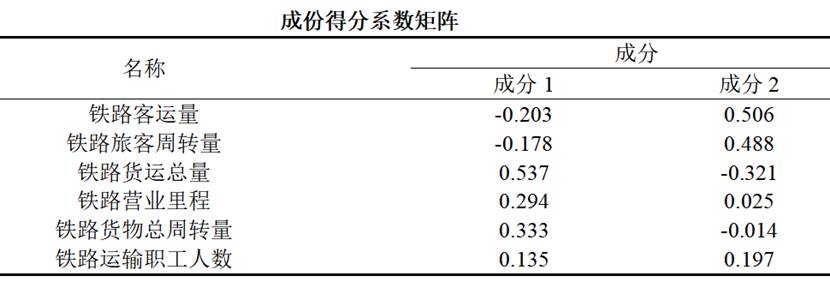
该表格提供了计算因子得分的系数，当我们希望得到每个样本的因子得分用于后续分析时，这个表格就变得非常重要。

5.碎石图

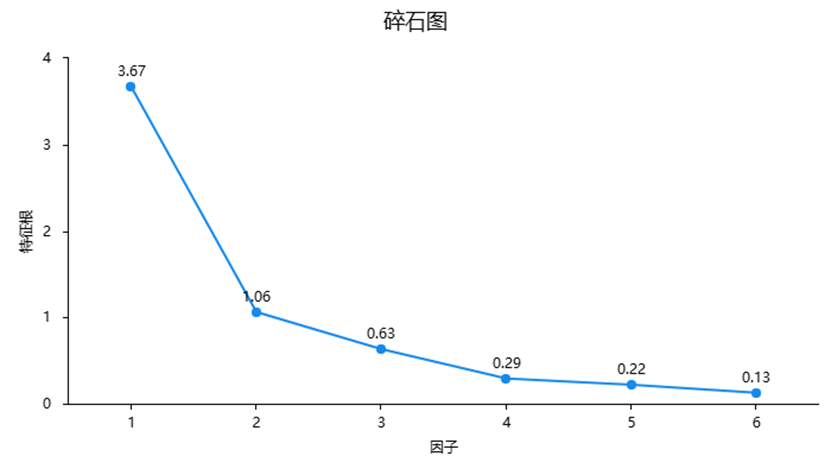
碎石图用于辅助判断因子提取个数，当拆线由陡峭突然变得平稳时，陡峭到平稳对应的因子个数即为参考提取因子个数。碎石图仅辅助决策因子个数，实际研究中更多以专业知识，结合因子与研究项对应关系情况，综合权衡判断得出因子个数。

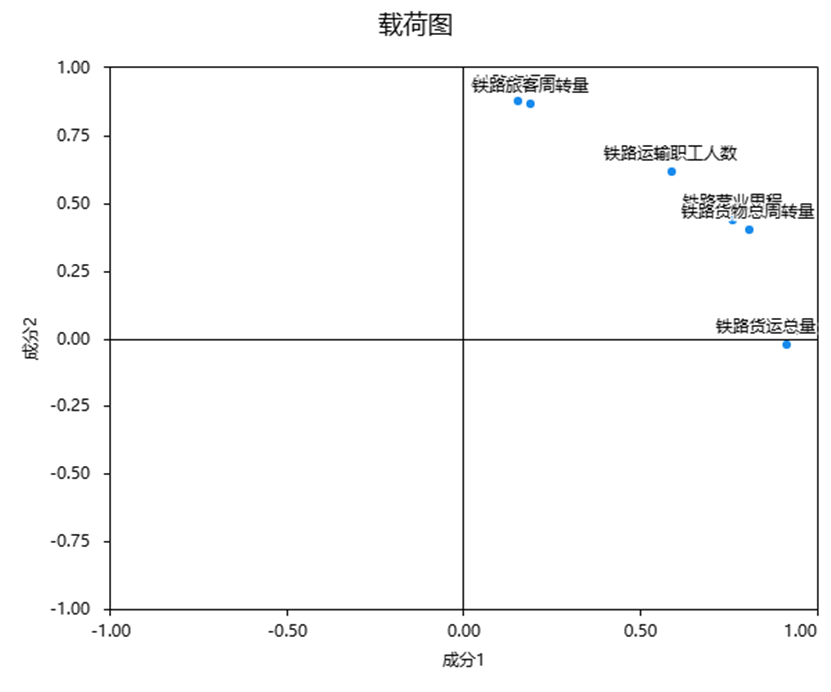
6.载荷图

载荷图用于展示各因子与载荷值关系情况，建议结合实际情况使用即可。

7. 线性组合系数及权重结果表

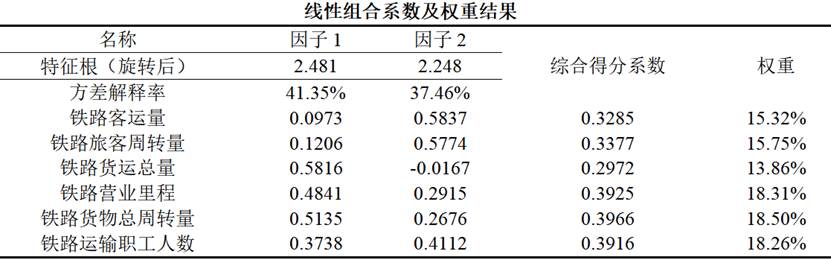
这个表格展示了各变量在综合得分中的权重分配，当我们需要计算综合得分或进行权重分析时，此表格提供必要的计算系数。

五、从“变量-因子”到“综合评分”：如何用输出做决策

确认研究目标：若目的是信息浓缩并解释潜在结构，优先关注载荷与共同度；若目的是构建复合指标或权重体系，则要重视成分得分系数与权重归一化步骤。
变量筛选原则：低共同度或低 MSA 的变量是删除候选；高交叉载荷需结合领域知识决定归属或删除；与其他变量高度冗余（相关 >0.8）则考虑合并或删减。
旋转策略选择：若理论认为潜因子独立，用 Varimax（最大方差法）；若因子可能相关，用斜交（Promax/Oblimin 等）以保留因子间相关信息。
权重与得分的解释限制：因子导出的权重基于线性组合与标准化数据，具有方法学合理性，但不是“真理”——应与理论、外部效度检验结果（例如回归或结构方程验证）一起解释。

六、探索性因子分析的方法学考量

1. 样本量的要求

探索性因子分析对样本量有明确要求，一般来说，样本量与变量数的比例至少应为5:1，即每个变量至少对应5个样本。理想情况下，总样本量应该达到300以上，这样才能保证因子分析结果的稳定性。

2. 因子数确定的策略