主成分分析结果中的“方差解释率”如何解读？

在主成分分析（PCA）中，“方差解释率”是一个非常重要的指标，它帮助我们理解每个主成分对原始数据变异性的解释能力。以下是关于“方差解释率”的详细解读：

1. 什么是方差解释率？

方差解释率表示每个主成分所解释的原始变量方差的百分比。它反映了主成分对原始数据变异性的贡献程度。通常，第一个主成分的方差解释率最高，后续主成分的方差解释率逐渐降低。

2. 如何计算方差解释率？

方差解释率是通过主成分的特征值来计算的。具体公式为：

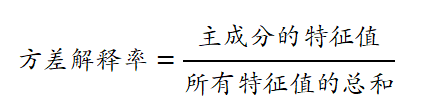
3. 如何解读方差解释率？

• 单个主成分的方差解释率：表示该主成分对原始数据变异性的解释能力。例如，如果第一个主成分的方差解释率为40%，则表示该主成分能够解释原始数据40%的变异性。
• 累计方差解释率：表示前几个主成分对原始数据变异性的累计解释能力。例如，如果前三个主成分的累计方差解释率为85%，则表示这三个主成分能够解释原始数据85%的变异性。

4. 如何选择主成分？

在实际应用中，我们通常会选择累计方差解释率达到一定阈值（如80%或85%）的主成分。这样可以确保所选的主成分能够保留原始数据的大部分信息，同时实现降维的目的。

5. SPSSAU中的操作步骤

在SPSSAU(在线SPSS)中进行主成分分析时，可以按照以下步骤操作： 

1. 上传数据：将需要进行主成分分析的数据上传到SPSSAU平台。 

2. 选择分析方法：在“进阶方法”模块中选择“主成分分析”。 

3. 设置参数：根据需求设置主成分的个数，通常选择累计方差解释率达到80%以上的主成分。 

4. 查看结果：分析完成后，查看“方差解释率”和“累计方差解释率”的结果，判断所选主成分的解释能力。

6. 实际应用示例

假设我们进行了一项市场调研，收集了10个指标的数据。通过主成分分析，我们得到了以下结果： 

- 第一个主成分的方差解释率为45% 

- 第二个主成分的方差解释率为30% 

- 第三个主成分的方差解释率为15% 累计方差解释率为90%。这意味着前三个主成分能够解释原始数据90%的变异性，因此我们可以选择这三个主成分进行后续分析。