Leetcode|线性序列|10. 正则表达式匹配（两字符串前均补1个相同字符）

1 动态规划

本题逻辑如下

[1] if 两字符相同(或遇到.通配符)则两索引i,j同步后移1位
[2] if 若两字符不同，且是因为遇到*通配符
——[2.1] *通配符前1位字符p[j-1]与s[i]相同 → (0次 || 多次匹配) eg.s = aaa, p = a*
——[2.2] *通配符前1位字符p[j-1]与s[i]不同 → 0次匹配 eg.s = aa, p = c*aa

大多数本题题解都用的递归实现动态规划，但本题我使用dp数组，其初始化比递归实现简洁不少，但其中细节并不简单，特此做以详细解释

1.1 dp数组含义

【dp数组含义】：s[0:i]和p[0:j]匹配的判断为bool dp[i][j]

1.2 为什么要在两字符串前同补1个相同字符？（判断*匹配需已知前2字符）

s = " " + s;
p = " " + p;

【原因】：判断*是否匹配需已知前2位，对于p = a*极端情况，需在两字符串前同补相同字符p = <空格>a*

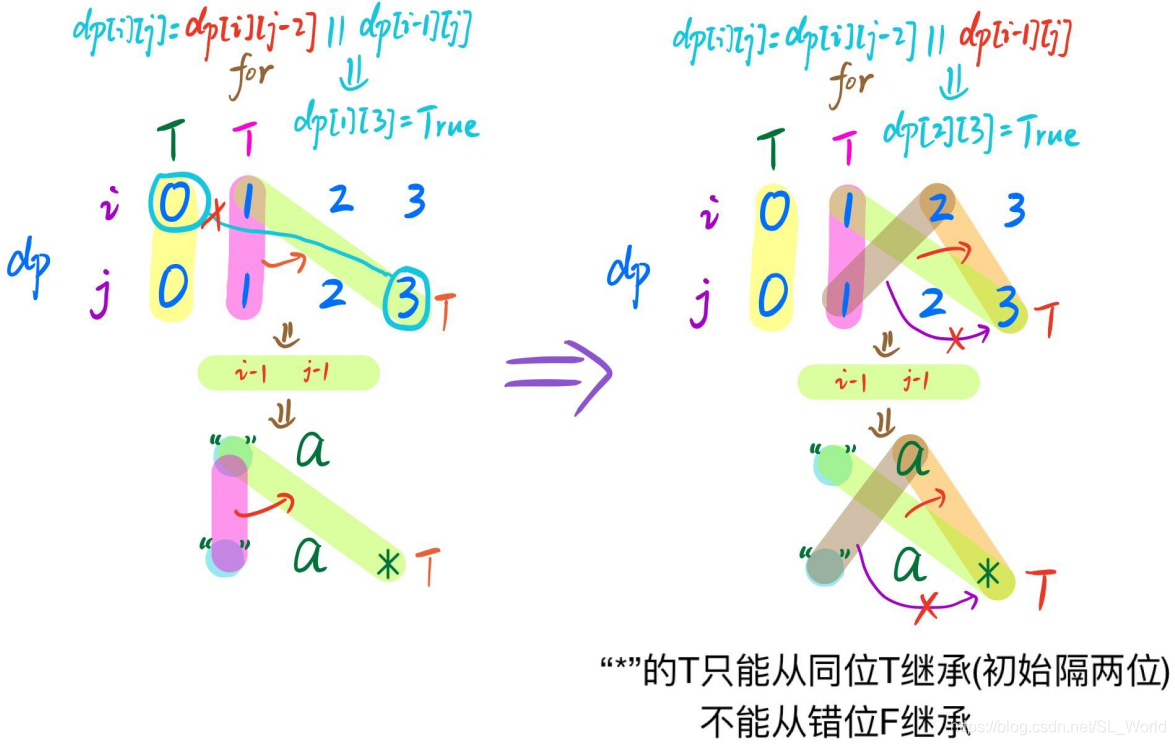
那为什么判断*是否匹配需已知前2位呢？具体见下图（从右往左看），其中上半部分是dp索引，下半部分是对应两字符串

• 0次匹配→dp[i][j - 2]
• 多次匹配→dp[i - 1][j]

【例子】s = a, p = a*

• 先看右图，对于dp[2][3]对应s[1] = a和p[2] = *情况，此时的*应匹配多次，所以dp[2][3]的True应来自匹配多次的dp[i - 1][j]而非匹配0次的dp[i][j - 2]。如果初始化dp[0][1] = dp[1][0] = True，则会误判s = a, p = c*情况为True
• 再看左图，对于dp[1][3]对应s[0] = <空格>和p[2] = *情况，此时的*应匹配0次，所以dp[1][3]的True应来自匹配0次的dp[i][j - 2]而非匹配多次的dp[i - 1][j]

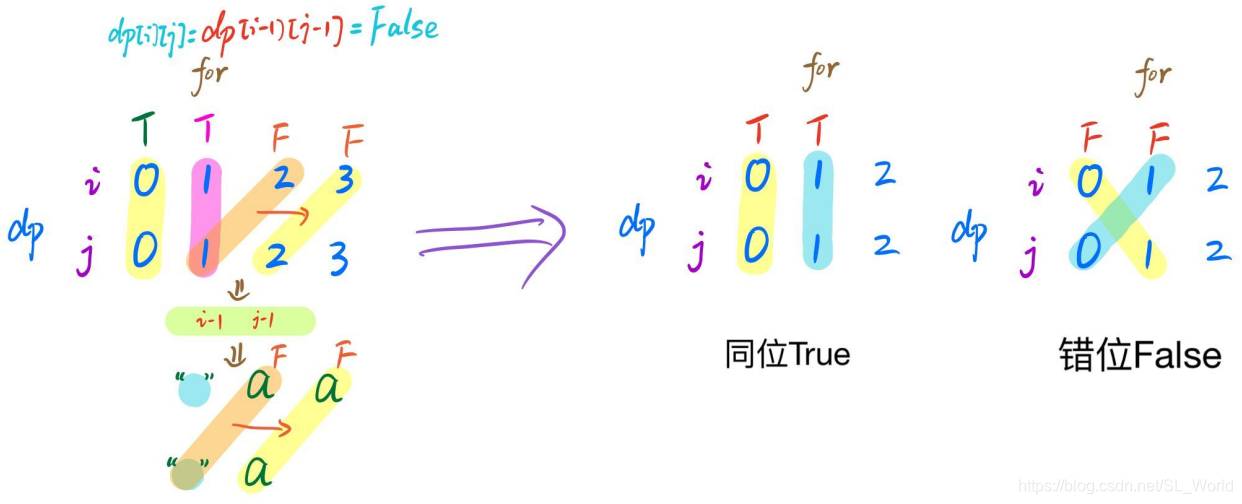
为什么一定要严格按照一开始的逻辑初始化，不能结果导向？如下图，只能同位字符为True，错位必须为False，否则会错误传递

class Solution {
public:
    bool isMatch(string s, string p) {
        // 判断"*"是否匹配需已知前2位，所以在两字符串前同补相同字符
        s = " " + s;
        p = " " + p;
        int asize = s.size();
        int bsize = p.size();
        // 通用初始化
        vector<vector<int>> dp(asize + 1, vector<int>(bsize + 1, false));
        // 边界初始化
        dp[0][0] = true;
        for (int i = 1; i <= asize; i++)
            for (int j = 1; j <= bsize; j++) {
                // 1.若两字符相同(或遇"."通配符)则两索引同步后移1位
                if (s[i - 1] == p[j - 1] || p[j - 1] == '.')
                    dp[i][j] = dp[i - 1][j - 1];
                // 2.若两字符不同是因为遇到"*"通配符
                else if (p[j - 1] == '*') {
                    // 2.1 "*"通配符前1位字符与s字符相同 -> (0次 || 多次匹配)
                    if (s[i - 1] == p[j - 2] || p[j - 2] == '.')
                        dp[i][j] = dp[i][j - 2] || dp[i - 1][j];
                    // 2.2 "*"通配符前1位字符与s字符不同 -> 0次匹配
                    else dp[i][j] = dp[i][j - 2];
                }
            }
        return dp[asize][bsize];
    }
};