Leetcode|651. 4键键盘（压缩成A和CV两键）

原创于 2021-03-26 21:24:02 发布 · 475 阅读

1 ·

CC 4.0 BY-SA版权

Leetcode动态规划专题专栏收录该内容

32 篇文章

订阅专栏

这篇博客探讨了一道关于使用动态规划求解按键优化问题的算法。文章指出，在给定的按键操作中，通过压缩问题到两种基本选择——按A键或使用Ctrl+V粘贴，可以找到最大化屏幕上A字符数量的策略。动态规划的状态转移方程为dp[i]=max(dp[i-1]+1,dp[j-2]*(i-j+1))，其中dp数组表示按键i次后屏幕上显示的A字符数。博客详细解析了状态和选择，并提供了实现代码。

在这里插入图片描述

动态规划

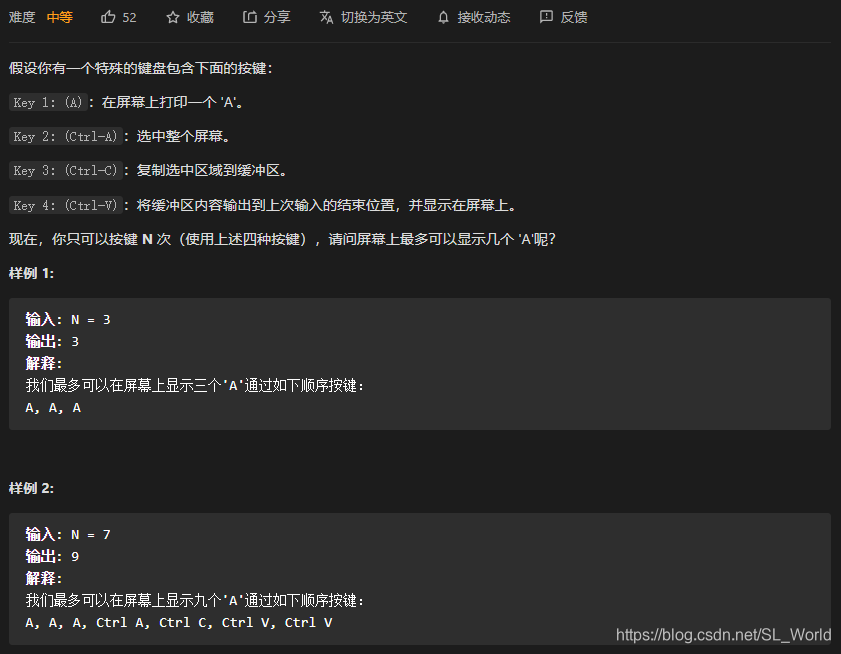
题目中提到的有四个按键，但实际上，我们可以压缩为2个选择，因为对于最优解，Ctrl+V一定在Ctrl+A-Ctrl+C两个按键后

【dp数组含义】：按键i次后屏幕显示dp[i]个A
【状态】：剩余可按键数量N
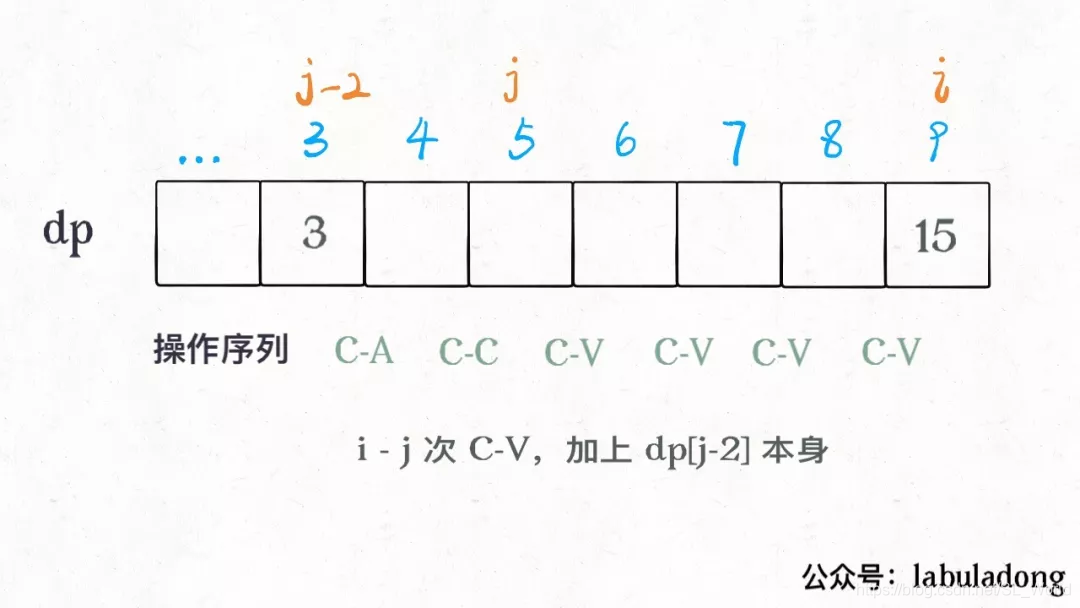
【选择】：①按A; ②按Ctrl+V（需通过额外变量j来确定Ctrl+C的位置，从而确定剪贴板中A的个数dp[j - 2]）
【状态转移方程】：dp[i] = max(dp[i - 1] + 1, dp[j - 2] * (i - j + 1));

在这里插入图片描述

class Solution {
public:
    int maxA(int N) {
        // dp数组含义：按键i次后屏幕显示dp[i]个A
        vector<int> dp(N + 1, 0);
        // 压缩为2个选择 → [1]按A;[2]按Ctrl-V (包含前方必有的Ctrl-A + Ctrl-C)
        for (int i = 1; i <= N; i++) {
            // [1]按A
            dp[i] = dp[i - 1] + 1;
            // [2]按Ctrl-V (包含前方必有的Ctrl-A + Ctrl-C)
            for (int j = 2; j < i; j++) 
                // dp[j - 2]表示剪贴板中A的个数，减去的2即为CA + CC两个组合键
                dp[i] = max(dp[i], dp[j - 2] * (i - j + 1)); // 最多可按(i - j + 1)个Ctrl-V
        }
        return dp[N];
    }
};