概述
只要是做过一点控制类的工程项目,对于时域、频域的相关概念一定不陌生,很可能还被折磨的死去活来。没错,我就是死去活来的那个。本人天资愚钝,信号处理等内容又是半路出家,没有系统的学习过,于是就被时域,频域,傅里叶变换,拉普拉斯变换等内容结结实实的胖揍了多年。举几个实际的工程需求吧,
- 如果使用软件编写一个一阶低通滤波器,如何根据截止频率 f c f_c fc设计不同的滤波系数 α \alpha α实现所需的滤波效果?
- 如何使用传递函数设计对应的控制器?
- …
记得第一次接触相关的内容,是研究生时学习信号与系统,本科时的学习偏重于软件工程相关的内容,对于控制类的内容接触几乎为零,当时的老师也默认每个人都有相关的功底,直接就跳过了基础环节,虽然课程考试通过了,但是不仅不知其然,也不知其所以然。幸好现在网络上有众多的大神们,以深入浅出的语言给出了诸多的介绍。本文即是从我实用的角度触发,汇集整理了一些相关的内容,也方便日后我重新回顾。
傅里叶变换
傅里叶变换的公式定义如下:对于任意一个满足狄里克莱条件的函数,可以通过以下变换将其从时域转到频域
F
(
ω
)
=
∫
−
∞
∞
f
(
t
)
e
−
j
ω
t
d
t
\displaystyle F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-j{\omega}t}dt
F(ω)=∫−∞∞f(t)e−jωtdt
这个公式需进一步说明的点是,
e
−
j
ω
t
e^{-j{\omega}t}
e−jωt和三角函数有什么关系?这里要引入一个新的名词,“虚指数”。
e
−
j
ω
t
e^{-j{\omega}t}
e−jωt就是虚指数,联系虚指数和三角函数的就是大名鼎鼎的欧拉公式
e
j
x
=
cos
(
x
)
+
j
sin
(
x
)
e^{jx}=\cos(x)+j\sin(x)
ejx=cos(x)+jsin(x)
不过在说明虚指数之前,先要了解的背景知识是傅里叶级数
傅里叶级数
傅里叶级数的具体推导过程可以参见此文傅里叶级数的推导。这里直接列出其表达式
f
(
t
)
=
a
0
2
+
∑
n
=
1
∞
[
a
n
cos
(
n
ω
0
t
)
+
b
n
sin
(
n
ω
0
t
)
]
a
0
=
2
T
∫
t
0
t
0
+
T
f
(
t
)
d
t
a
n
=
2
T
∫
t
0
t
0
+
T
f
(
t
)
cos
(
n
ω
0
t
)
d
t
b
n
=
2
T
∫
t
0
t
0
+
T
f
(
t
)
sin
(
n
ω
0
t
)
d
t
\displaystyle \begin{align*} f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}[a_n\cos(n\omega_0 t)+b_n\sin(n\omega_0 t)] \\a_0&=\frac{2}{T}\int_{t_0}^{t_0+T}f(t)dt \\a_n&=\frac{2}{T}\int_{t_0}^{t_0+T}f(t)\cos(n\omega_0 t)dt \\b_n&=\frac{2}{T}\int_{t_0}^{t_0+T}f(t)\sin(n\omega_0 t)dt \end{align*}
f(t)a0anbn=2a0+n=1∑∞[ancos(nω0t)+bnsin(nω0t)]=T2∫t0t0+Tf(t)dt=T2∫t0t0+Tf(t)cos(nω0t)dt=T2∫t0t0+Tf(t)sin(nω0t)dt
注意,在此表达式里,为了统一
a
0
,
a
n
,
b
n
a_0,a_n,b_n
a0,an,bn前面的系数为
2
T
\frac{2}{T}
T2,在傅里叶级数里直流常量的定义是
a
0
2
\frac{a_0}{2}
2a0,有的表达式里,直流常量使用的是
a
0
a_0
a0,此时对应的
a
0
a_0
a0表达式为
a
0
=
1
T
∫
t
0
t
0
+
T
f
(
t
)
d
t
a_0=\frac{1}{T}\int_{t_0}^{t_0+T}f(t)dt
a0=T1∫t0t0+Tf(t)dt。
在傅里叶级数的推导过程里,还用到了几个必要的概念,麦克劳林待定系数法,以及三角函数的正交性,具体可以参见傅里叶级数的推导。
虚指数 e − j ω t e^{-j{\omega}t} e−jωt的引入
使用欧拉公式
e
j
x
=
cos
(
x
)
+
j
sin
(
x
)
e^{jx}=\cos(x)+j\sin(x)
ejx=cos(x)+jsin(x)将三角函数改写成如下
sin
(
n
ω
t
)
=
e
j
n
ω
0
t
−
e
−
j
n
ω
0
t
2
j
cos
(
n
ω
t
)
=
e
j
n
ω
0
t
+
e
−
j
n
ω
0
t
2
\displaystyle \sin(n\omega t)=\frac{e^{jn\omega_0 t}-e^{-jn\omega_0 t}}{2j} \\\cos(n\omega t)=\frac{e^{jn\omega_0 t}+e^{-jn\omega_0 t}}{2}
sin(nωt)=2jejnω0t−e−jnω0tcos(nωt)=2ejnω0t+e−jnω0t
将两式代入傅里叶级数可得
f ( t ) = a 0 2 + ∑ n = 1 ∞ [ a n − j b n 2 e j n ω 0 t + a n + j b n 2 e − j n ω 0 t ] \displaystyle f(t)=\frac{a_0}{2}+\sum_{n=1}^{\infty}[\frac{a_n -jb_n}{2}e^{jn\omega_0 t}+\frac{a_n +jb_n}{2}e^{-jn\omega_0 t}] f(t)=2a0+n=1∑∞[2an−jbnejnω0t+2an+jbne−jnω0t]
从
a
n
a_n
an和
b
b
b_b
bb的定义可以得到
a
−
n
=
2
T
∫
t
0
t
0
+
T
f
(
t
)
cos
(
−
n
ω
0
t
)
d
t
=
a
n
b
−
n
=
2
T
∫
t
0
t
0
+
T
f
(
t
)
sin
(
−
n
ω
0
t
)
d
t
=
−
b
n
\displaystyle a_{-n}=\frac{2}{T}\int_{t_0}^{t_0+T}f(t)\cos(-n\omega_0 t)dt=a_n \\b_{-n}=\frac{2}{T}\int_{t_0}^{t_0+T}f(t)\sin(-n\omega_0 t)dt=-b_n
a−n=T2∫t0t0+Tf(t)cos(−nω0t)dt=anb−n=T2∫t0t0+Tf(t)sin(−nω0t)dt=−bn
于是引入虚指数的傅里叶级数可以进一步转化为
f
(
t
)
=
a
0
2
+
∑
n
=
1
∞
[
a
n
−
j
b
n
2
e
j
n
ω
0
t
+
a
n
+
j
b
n
2
e
−
j
n
ω
0
t
]
=
a
0
2
+
∑
n
=
1
∞
[
a
n
−
j
b
n
2
e
j
n
ω
0
t
]
+
∑
n
=
−
∞
−
1
[
a
−
n
+
j
b
−
n
2
e
j
n
ω
0
t
]
=
a
0
2
+
∑
n
=
1
∞
[
a
n
−
j
b
n
2
e
j
n
ω
0
t
]
+
∑
n
=
−
∞
−
1
[
a
n
−
j
b
n
2
e
j
n
ω
0
t
]
\displaystyle \begin{align*} f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}[\frac{a_n -jb_n}{2}e^{jn\omega_0 t}+\frac{a_n +jb_n}{2}e^{-jn\omega_0 t}] \\&=\frac{a_0}{2}+\sum_{n=1}^{\infty}[\frac{a_n -jb_n}{2}e^{jn\omega_0 t}]+\sum_{n=-\infty}^{-1}[\frac{a_{-n} +jb_{-n}}{2}e^{jn\omega_0 t}] \\&=\frac{a_0}{2}+\sum_{n=1}^{\infty}[\frac{a_n -jb_n}{2}e^{jn\omega_0 t}]+\sum_{n=-\infty}^{-1}[\frac{a_{n} -jb_{n}}{2}e^{jn\omega_0 t}]\end{align*}
f(t)=2a0+n=1∑∞[2an−jbnejnω0t+2an+jbne−jnω0t]=2a0+n=1∑∞[2an−jbnejnω0t]+n=−∞∑−1[2a−n+jb−nejnω0t]=2a0+n=1∑∞[2an−jbnejnω0t]+n=−∞∑−1[2an−jbnejnω0t]
此时
a n − j b n 2 = 1 T [ ∫ t 0 t 0 + T f ( t ) cos ( n ω 0 t ) d t − j ∗ ∫ t 0 t 0 + T f ( t ) sin ( n ω 0 t ) d t ] = 1 T ∫ t 0 t 0 + T f ( t ) [ cos ( n ω 0 t ) − j ∗ sin ( n ω 0 t ) ] d t = 1 T ∫ t 0 t 0 + T f ( t ) [ e j n ω 0 t + e − j n ω 0 t 2 − j ∗ e j n ω 0 t − e − j n ω 0 t 2 j ] d t = 1 T ∫ t 0 t 0 + T f ( t ) e − j n ω 0 t d t \displaystyle \begin{align*} \frac{a_n -jb_n}{2}&=\frac{1}{T}[\int_{t_0}^{t_0+T}f(t)\cos(n\omega_0 t)dt-j*\int_{t_0}^{t_0+T}f(t)\sin(n\omega_0 t)dt] \\&=\frac{1}{T}\int_{t_0}^{t_0+T}f(t)[\cos(n\omega_0 t)-j*\sin(n\omega_0 t)]dt \\&=\frac{1}{T}\int_{t_0}^{t_0+T}f(t)[\frac{e^{jn\omega_0 t}+e^{-jn\omega_0 t}}{2}-j*\frac{e^{jn\omega_0 t}-e^{-jn\omega_0 t}}{2j}]dt \\&=\frac{1}{T}\int_{t_0}^{t_0+T}f(t)e^{-jn\omega_0 t}dt\end{align*} 2an−jbn=T1[∫t0t0+Tf(t)cos(nω0t)dt−j∗∫t0t0+Tf(t)sin(nω0t)dt]=T1∫t0t0+Tf(t)[cos(nω0t)−j∗sin(nω0t)]dt=T1∫t0t0+Tf(t)[2ejnω0t+e−jnω0t−j∗2jejnω0t−e−jnω0t]dt=T1∫t0t0+Tf(t)e−jnω0tdt
将 a 0 , a n − j b n 2 a_0,\frac{a_n -jb_n}{2} a0,2an−jbn的公式全部代入得到傅里叶级数可得
f ( t ) = a 0 2 + ∑ n = 1 ∞ [ a n − j b n 2 e j n ω 0 t ] + ∑ n = − ∞ − 1 [ a n − j b n 2 e j n ω 0 t ] = 1 T ∫ t 0 t 0 + T f ( t ) d t + ∑ n = 1 ∞ 1 T ∫ t 0 t 0 + T f ( t ) e − j n ω 0 t d t ∗ e j n ω 0 t + ∑ n = − ∞ − 1 1 T ∫ t 0 t 0 + T f ( t ) e − j n ω 0 t d t ∗ e j n ω 0 t = 1 T ∑ n = − ∞ ∞ ∫ t 0 t 0 + T f ( t ) e − j n ω 0 t d t ∗ e j n ω 0 t \displaystyle \begin{align*} f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}[\frac{a_n -jb_n}{2}e^{jn\omega_0 t}]+\sum_{n=-\infty}^{-1}[\frac{a_{n} -jb_{n}}{2}e^{jn\omega_0 t}] \\&=\frac{1}{T}\int_{t_0}^{t_0+T}f(t)dt+\sum_{n=1}^{\infty}\frac{1}{T}\int_{t_0}^{t_0+T}f(t)e^{-jn\omega_0 t}dt*e^{jn\omega_0 t}+\sum_{n=-\infty}^{-1}\frac{1}{T}\int_{t_0}^{t_0+T}f(t)e^{-jn\omega_0 t}dt*e^{jn\omega_0 t} \\&=\textcolor{blue}{\frac{1}{T}\sum_{n=-\infty}^{\infty}\int_{t_0}^{t_0+T}f(t)e^{-jn\omega_0 t}dt*e^{jn\omega_0 t}} \end{align*} f(t)=2a0+n=1∑∞[2an−jbnejnω0t]+n=−∞∑−1[2an−jbnejnω0t]=T1∫t0t0+Tf(t)dt+n=1∑∞T1∫t0t0+Tf(t)e−jnω0tdt∗ejnω0t+n=−∞∑−1T1∫t0t0+Tf(t)e−jnω0tdt∗ejnω0t=T1n=−∞∑∞∫t0t0+Tf(t)e−jnω0tdt∗ejnω0t
当 n = 0 时, 1 T ∫ t 0 t 0 + T f ( t ) e − j n ω 0 t d t ∗ e j n ω 0 t = 1 T ∫ t 0 t 0 + T f ( t ) d t 当n=0时,\frac{1}{T}\int_{t_0}^{t_0+T}f(t)e^{-jn\omega_0 t}dt*e^{jn\omega_0 t}=\frac{1}{T}\int_{t_0}^{t_0+T}f(t)dt 当n=0时,T1∫t0t0+Tf(t)e−jnω0tdt∗ejnω0t=T1∫t0t0+Tf(t)dt
此蓝色公式即为傅里叶级数的虚指数表达形式。令
【这里需要进一步补充如何将周期T推广到无限的情况】
傅里叶级数和变换的区别
- 傅立叶级数对应的是周期信号,而傅立叶变换则对应的是一个时间连续可积信号(不一定是周期信号)
- 傅立叶级数要求信号在一个周期内能量有限,而后者则要求在整个区间能量有限
- 傅立叶级数的对应是离散的,而傅立叶变换则对应是连续的。
故而,两者的物理含义不同,且其量纲也是不同的, F ( j k w ) F(jkw) F(jkw)代表周期信号的第k次谐波幅度的大小,而 F ( j w ) F(jw) F(jw)则是频谱密度的概念。所以答案是这两者从本质上不是一个概念,傅立叶级数是周期信号的另一种时域的表达方式,也就是正交级数,它是不同的频率的波形的时域叠加。而傅立叶变换则是完全的频域分析,傅里叶级数适用于对周期性现象做数学上的分析,傅里叶变换可以看作傅里叶级数的极限形式,也可以看作是对周期现象进行数学上的分析,同时也适用于非周期性现象的分析。
傅里叶级数和变换的一点感悟
抛开具体数学公式,这里试图从感性的角度来认知傅里叶变换。
首先,傅里叶变换和其逆变换不是定理,而是人为定义的两个公式,其作用是可以将函数从时域变换到频域,这个前提假设非常重要。
因为这涉及到了一个很有意思的点,时域和频域也是人为定义的两个“域”概念,如果脑洞大一点,用近世代数的群环域的概念去套用(需特别说明,这里的脑洞没有理论证明过),“域”这个概念,代表的是由其定义的基元素以及基于基元素定义的符合“加减乘除”运算规律(如加法交换律,乘法分配律等)的一类元素和运算集合。于是,时域里,基元素和“加减乘除”都是我们常规认知的运算(姑且称其为常规域),而频域里,基元素是不同频率的正弦函数,而将此基元素由三个因素确定(频率,幅值和相位),比如在频域里的“乘法”,对应的常规域的运算就是卷积。所以,第一个感性认知是,傅里叶变换和其逆变换是一种数学工具,是为了转换运算域而定义的数学工具,不是公理。
其次,因为选取的域是以正弦函数为基元素的(余弦函数可以转化为等价的正弦函数,因此下述讨论统一使用正弦函数),那么根据傅里叶级数的定义,任何一个周期为T的函数f(t),都可以拆解成为一组正弦函数的叠加,这里就需要确定每一个正弦函数的三要素(频率,幅值和相位)。其中,频率可以用遍历的方式从小到大,而幅值和相位就是需要确定的值。根据三角函数的正交性(即不同频率的两个三角函数,其乘积在一个周期内的积分值为0,参考文章【1】),用一个固定频率 ω n \omega_n ωn的正弦函数和余弦函数去乘以周期函数f(t),然后再在一个周期内对其乘积结果做积分,所有非相同频率的基分量,其与 ω n \omega_n ωn的正弦函数和余弦相乘后的积分都是零,只有同频的基会留下来,此时就实现了对于指定基元素的幅值和相位的抽取,从而得到了这一个基元素的三要素(频率 ω n \omega_n ωn,幅值 A n A_n An,相位 ϕ n \phi_n ϕn)。如果让n的取值是正整数,就得到了离散傅里叶级数的各个频率点所需数值;如果让n取值为正实数(此时相当于周期T为无穷大,让频谱之间的间隔小到称为连续的实数),就变成了连续傅里叶变换。
回顾欧拉公式 e j x = cos ( x ) + j sin ( x ) e^{jx}=\cos(x)+j\sin(x) ejx=cos(x)+jsin(x),其恰好包含了所需的正弦基与余弦基,更因为虚数的引入,包含了角度信息(旋转操作),因此这就是傅里叶变换里为什么使用了虚指数,因为虚指数既包含了数值信息,又包含了角度(相位)信息。
当认识到以上两件事之后,再来看傅里叶变换后的结果,存在频率谱,相位谱就不足为奇了,因为每一个基元素都需要三要素(频率,幅值,相位),其中频率谱就是以频率为横轴,幅值为纵轴,而相位谱是以频率为横轴,相位为纵轴,三者合一就可以表示任意一个基元素。
几个不错的文章
【1】傅里叶变换推导详解
【2】傅里叶系列(一)傅里叶级数的推导
【3】信号的傅里叶变换后的虚数怎样理解?
【4】傅里叶级数
【5】傅里叶分析之掐死教程(完整版)更新于2014.06.06
【6】【从原理的视角】傅里叶级数以及三角表达式、虚指数表达式,Matlab仿真程序
【7】一幅图弄清DFT与DTFT,DFS的关系
拉普拉斯变换
傅里叶变换强调函数要满足绝对可积,感性理解这个要求,即在正无穷的远端,函数要趋向x轴以便积分值收敛。对于不满足上述要求的函数f(t),可以考虑将其乘以一个衰减函数
e
−
σ
t
e^{-\sigma t}
e−σt,使得
f
(
t
)
e
−
σ
t
f(t)e^{-\sigma t}
f(t)e−σt满足绝对可积的要求,从而可以对
f
(
t
)
e
−
σ
t
f(t)e^{-\sigma t}
f(t)e−σt进行傅里叶变换,同时为了保证
e
−
σ
t
e^{-\sigma t}
e−σt一直为衰减函数,将t的定义域缩减到正半轴,此时的公式为
F
(
f
(
t
)
e
−
σ
t
)
=
∫
0
∞
f
(
t
)
e
−
σ
t
e
−
j
ω
t
d
t
=
∫
0
∞
f
(
t
)
e
−
(
σ
+
j
ω
)
t
d
t
\displaystyle \begin{align*} F(f(t)e^{-\sigma t})&=\int_{0}^{\infty}f(t)e^{-\sigma t}e^{-j{\omega}t}dt \\&=\int_{0}^{\infty}f(t)e^{-(\sigma+j\omega) t}dt \end{align*}
F(f(t)e−σt)=∫0∞f(t)e−σte−jωtdt=∫0∞f(t)e−(σ+jω)tdt
令 s = σ + j ω s=\sigma+j\omega s=σ+jω,则上式就可以变成
F ( s ) = ∫ 0 ∞ f ( t ) e − s t d t \displaystyle F(s)=\int_{0}^{\infty}f(t)e^{-st}dt F(s)=∫0∞f(t)e−stdt
这就是拉普拉斯变换。
拉普拉斯变换解决了不满足绝对可积条件的连续信号,变换到频率域的问题,同时也对“频率”的定义进行了扩充。拉普拉斯变换与连续时间傅里叶变换的关系是:拉普拉斯变换将频率从实数推广为复数,因而傅里叶变换变成了拉普拉斯变换的一个特例。当s为纯虚数时,f(t)的拉普拉斯变换,即为f(t)的傅里叶变换。
关于拉普拉斯变换的收敛域问题,可以参见此文章傅里叶变换到拉普拉斯变换及收敛域分析。这个视频也对拉普拉斯变换做了比较好的介绍「珂学原理」No. 26「拉普拉斯变换了什么?」。
Z变换
Z变换本质上是拉普拉斯变换的离散形式。那么Z变换的意义在于什么呢?在数字信号处理以及数字控制系统中,Z变换提供了数学基础。利用Z变换很快就能将一个传递函数描述成差分方程形式,这就为编程实现提供了数学依据,比如一个数字滤波器知道其Z变换形式,写代码就是分分钟的事情了,同样知道一个控制算法的Z变换形式,同样编代码也是水到渠成的事情。详见此文章
傅里叶变换、拉普拉斯变换、Z 变换的联系是什么?为什么要进行这些变换?
总结
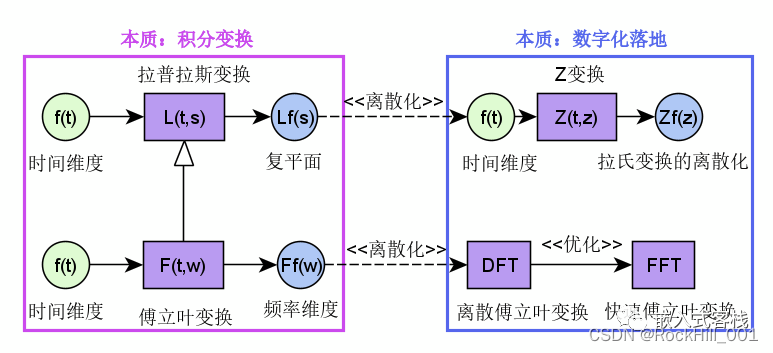
要理解三种变换的联系区别,首先要理解什么是数学变换,什么是积分变换。傅立叶变换以及拉普拉斯变换本质上都是连续或有限个第一类间断点函数的积分变换,而傅立叶变换是拉普拉斯变换的特殊形式,而Z变换是拉普拉斯变换的离散形式。每种变换都有其应用价值,傅立叶变换在信号处理的频域分析中提供了强大的数学工具,而拉普拉斯变换在电子学、控制工程、航空航天等领域提供了建模、分析的数学分析工具;Z变换则将这些变换进而落地为数字实现提供数学理论依据。DFT为FFT的离散化形式,而FFT是DFT的算法优化实现。
参考文献
To Do List
频谱,相位谱,功率谱的进一步理解
信号频域分析方法的理解(频谱、能量谱、功率谱、倒频谱、小波分析)
各种谱函数的区别是什么,何时用何种函数?
傅里叶变换与微分方程的相互关系
微分方程(1)-基本概念及分类
补充:微分方程的定义和分类
频率响应分析
为何在传递函数中,可以用jw 替换s
一文讲透一阶系统的系统响应、传递函数和输出响应
一文带你通俗理解幅频响应和相频响应
微分方程(2)-一阶常微分方程的解法
单位冲激响应的测量方法
传递函数与z变换的关系
传递函数转化为差分方程
S域传递函数——Z域传递函数——差分方程的转换方法
传递函数,Z变换与差分方程之间的转化
s域传递函数变为z域传递函数
s域和z域变换笔记
滤波器的设计
低通滤波器的设计与工程实现
一阶低通滤波器软件算法
功率谱密度
对于一个随机信号而言,时域信息是杂乱无章的,唯一的确定性信息但是在统计意义下得到的,即幅值呈正太分布,均方值也就是平均功率是固定的。根据帕斯瓦定理,信号的平均功率在时域和频域是守恒的,按道理说直接对时域信号进行傅里叶变换再取平方就可以。但不幸的事,随机信号的不满足傅里叶变换绝对值可积的条件,严格意义傅里叶变换不存在,于是发明了自相关函数的概念,将信号的蕴含的周期信号识别出来,并将相位信息去掉(相位不影响平均功率),于是就出现了我们在教材上见到的最终形式维纳-辛钦定理:一个信号的功率密度谱,就是其自相关函数的傅里叶变换。提炼一下就是:随机信号→幅值正太分布→均方值(平均功率)→帕斯瓦定理(功率守恒)→自相关函数(去除相位信息)→维纳-辛钦定理(最终形式)
功率谱密度(PSD)
如何理解随机振动的功率谱密度? (非常好的文章)
为什么随机信号不能用频谱表示?而必须用功率谱密度表示呢?
能量信号和功率信号的分别
卷积,自相关和互相关
如何通俗易懂地解释卷积? (非常棒的文章)
卷积、互相关与自相关
控制系统
自控学习笔记系列























 10万+
10万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








